【笔记】Encoder-Decoder模型
Encoder-Decoder Framework
- Encoder-Decoder
-
- Encoder
- Decoder
- Decoder with Attention
- 参考
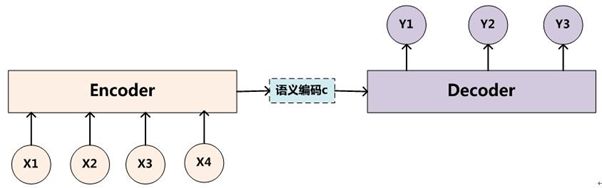
Encoder-Decoder
Encoder
输入: X = ( x 1 , x 2 , . . . , x T x ) X=(x_1, x_2, ..., x_{T_x}) X=(x1,x2,...,xTx)
输出: 上下文向量(context vector) c c c
步骤:
h t = f ( x t , h t − 1 ) c = q ( { h 1 , . . . , h T x } ) (1) h_t=f(x_t,h_{t-1}) \\ c=q(\{h_1,..., h_{T_x}\}) \tag{1} ht=f(xt,ht−1)c=q({h1,...,hTx})(1)
其中, h t ∈ R n h_t\in \R^n ht∈Rn 表示t时刻的隐含状态;c表示由隐含状态序列得到的向量;f, q 是非线性模型
举例:Sutskever et al. Sequence to sequence learning with neural networks(NIPS, 2014)
使用 h t = L S T M ( x t , h t − 1 ) , c = h T x h_t=LSTM(x_t,h_{t-1}) , c=h_{T_x} ht=LSTM(xt,ht−1),c=hTx
Decoder
目的:预测下一个翻译出来的词 y t y_{t} yt
输入: c c c,之前预测出来的词 { y 1 , . . . , y t − 1 } \{y_1,..., y_{t-1}\} {y1,...,yt−1}
步骤:用条件概率表示
p ( y ) = ∏ t = 1 T p ( y t ∣ { y 1 , . . . , y t − 1 } , c ) , y = ( y 1 , . . . , y T y ) (2) p(\boldsymbol{y})=\prod^T_{t=1}p(y_t|\{y_1,..., y_{t-1}\},c) ,\boldsymbol{y}=(y_1,...,y_{T_y}) \tag{2} p(y)=t=1∏Tp(yt∣{y1,...,yt−1},c),y=(y1,...,yTy)(2)
如果使用RNN族,那么条件概率写为
p ( y t ∣ { y 1 , . . . , y t − 1 } , c ) = g ( y t − 1 , s t , c ) p(y_t|\{y_1,..., y_{t-1}\} ,c)=g(y_{t-1},s_t,c) p(yt∣{y1,...,yt−1},c)=g(yt−1,st,c)
其中,g是非线性模型;s为隐藏层; s t = f ( s t − 1 , y t − 1 , c ) s_t=f(s_{t-1},y_{t-1},c) st=f(st−1,yt−1,c)
Decoder with Attention
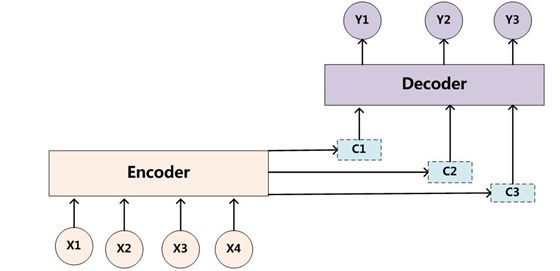
对公式(2)中定义的条件概率进行修改
p ( y i ∣ { y 1 , . . . , y i − 1 } , X ) = g ( y i − 1 , s t , c i ) p(y_i|\{y_1,..., y_{i-1}\} ,X)=g(y_{i-1},s_t,c_i) p(yi∣{y1,...,yi−1},X)=g(yi−1,st,ci)
参考
[1] https://blog.csdn.net/u014595019/article/details/52826423