再做leetcode42hard题接雨水——双指针法

再做leetcode42hard题接雨水——双指针法

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1：

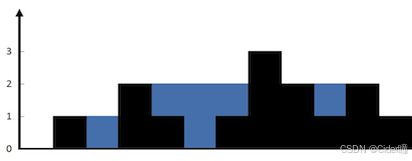
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：
输入：height = [4,2,0,3,2,5]
输出：9

提示：
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

题目分析

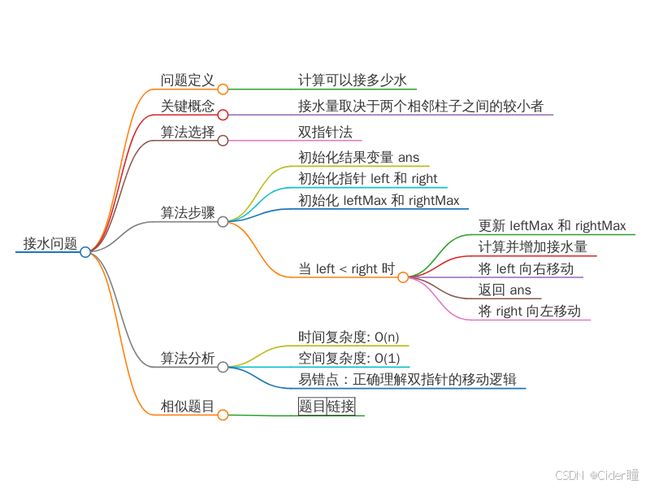
• 问题定义：计算可以接多少水。
• 关键概念：接水量取决于两个相邻柱子之间的较小者。

算法介绍

• 双指针法：使用两个指针分别从数组的开始和结束向中间移动，同时更新左侧和右侧的最高柱子高度。

算法步骤

1. 初始化结果变量ans为0，表示可以接的水量。
2. 初始化两个指针left和right，分别指向数组的开始和结束。
3. 初始化两个变量leftMax和rightMax，分别表示左侧和右侧的最高柱子高度。
4. 当left小于right时，进行以下操作：
   • 更新leftMax为leftMax和height[left]中的较大值。
   • 更新rightMax为rightMax和height[right]中的较大值。
   • 如果leftMax小于rightMax，则说明对于位置left来说，其左侧最高点一定小于右侧真正最高点，所以可以计算接水量，并将left向右移动。
   • 如果leftMax不小于rightMax，则说明对于位置right来说，其右侧最高点一定小于或等于左侧最高点，所以可以计算接水量，并将right向左移动。
5. 返回ans，即可以接的水量。

算法流程

是

是

否

初始化结果变量 ans

初始化指针 left 和 right

初始化 leftMax 和 rightMax

left < right?

更新 leftMax 和 rightMax

leftMax < rightMax?

计算并增加接水量

将 left 向右移动

返回 ans

将 right 向左移动

具体代码

//双指针法：!!对于位置 i 的接水量取决于其左侧最高点leftMax 和右侧最高点rightMax 中的较小者!!
//使用 height[left] 和 height[right] 更新 leftMax, rightMax
class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        int left = 0, right = height.size() - 1;
        int leftMax = 0, rightMax = 0;
        while (left < right) {
            leftMax = max(leftMax, height[left]);
            rightMax = max(rightMax, height[right]);
            if (leftMax < rightMax) {
//若 leftMax < rightMax, 则说明对于位置 left 来说, 已经可以定：其左侧最高点一定小于右侧真正最高点
                ans += leftMax - height[left];
                ++left;
            } else {
                ans += rightMax - height[right];
                --right;
            }
        }
        return ans;
    }
};

算法分析

• 时间复杂度：O(n)，其中n是数组的长度。
• 空间复杂度：O(1)，只需要常数级别的额外空间。
• 易错点：正确理解双指针的移动逻辑，特别是如何根据两侧的高度更新指针。

相似题目

题目	链接
42. 接雨水	LeetCode
173. 二进制搜索树迭代器	LeetCode
146. LRU缓存机制	LeetCode