代码随想录算法训练营第26天|491.递增子序列、46.全排列、47.全排列 II、332.重新安排行程、51. N皇后、37. 解数独
目前仍在补,已经是一周左右的进度差,但我有我的节奏!
最后三道题超难!!!
打卡Day26
- 1.491.递增子序列
- 2.46.全排列
- 3.47.全排列 II
- 4.332.重新安排行程
- 5.51. N皇后
- 6.37. 解数独
1.491.递增子序列
题目链接:491.递增子序列
文档讲解: 代码随想录
在搜索的过程中就判断,递增才能进入递归。与90.子集II不同的是,去重不能通过排序来进行。
class Solution(object):
def findSubsequences(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res = []
self.backtracking(nums, 0, res, [])
return res
def backtracking(self, nums, startindex, res, path):
if len(path) > 1:
res.append(path[:])
#定义集合进行记录每层遍历过的元素
uset = set()
for i in range(startindex, len(nums)):
if nums[i] in uset:
continue
if path and nums[i] < path[-1]:
continue
uset.add(nums[i])
path.append(nums[i])
self.backtracking(nums, i + 1, res, path)
path.pop()
class Solution(object):
def findSubsequences(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res = []
self.backtracking(nums, 0, res, [])
return res
def backtracking(self, nums, startindex, res, path):
if len(path) > 1:
res.append(path[:])
used = [0] * 201 #题目中有说明数组长度
for i in range(startindex, len(nums)):
if used[nums[i] + 100] == 1 or (path and nums[i] < path[-1]):
continue
used[nums[i] + 100] = 1
path.append(nums[i])
self.backtracking(nums, i + 1, res, path)
path.pop()
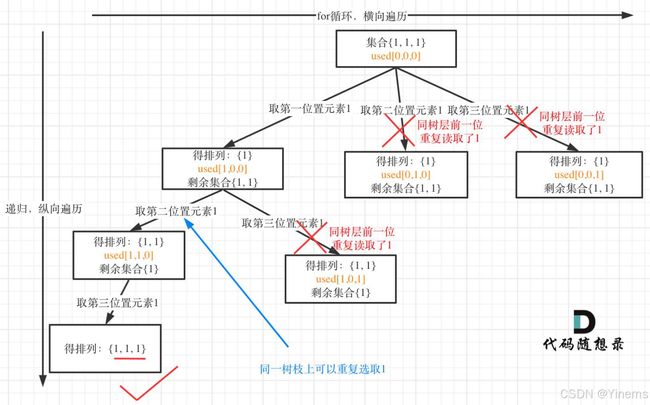
2.46.全排列
题目链接:491.递增子序列
文档讲解: 代码随想录
需要uesd数组记录path中都放了哪些元素。
class Solution(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res = []
used = [False] * len(nums)
self.backtracking(nums, res, [], used)
return res
def backtracking(self, nums, res, path, used):
if len(path) == len(nums):
res.append(path[:])
for i in range(len(nums)):
if used[i]:
continue
used[i] = True
path.append(nums[i])
self.backtracking(nums, res, path, used)
path.pop()
used[i] = False
3.47.全排列 II
题目链接:47.全排列 II
文档讲解: 代码随想录
终止条件是,path 的长度和 nums 的长度相同。单层逻辑, 这道题应该可以先排个序,然后,去重是根据uesd数组来判断。
class Solution(object):
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
res = []
nums.sort()
used = [False] * len(nums)
self.backtracking(nums, res, [], used)
return res
def backtracking(self, nums, res, path, used):
#终止条件
if len(path) == len(nums):
res.append(path[:])
return
for i in range(len(nums)):
#去重
if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
continue
if used[i]:
continue
path.append(nums[i])
used[i] = True
self.backtracking(nums, res, path, used)
path.pop()
used[i] = False
注意点:
if i > 0 and nums[i] == nums[i - 1] and not used[i - 1]:
continue
判断used[i - 1]可以有两种思路,一种是从树枝上去重,则判断为真则跳过。

另一种是在树层上去重,判断为假则跳过。
这里虽然可以写成 and used[i - 1],但是一定要一起判断used[i - 1],因为要一直是 true 或者一直是false 才可以,而不是 一会是true 一会又是false。
4.332.重新安排行程
题目链接:332.重新安排行程
文档讲解: 代码随想录
这道题有几个难点:
(1)一个行程中,如果航班处理不好就容易变成一个圈,成为死循环
因为出发机场和到达机场是会有重复的
(2)有多种解法,字母排序靠前,需要记录映射关系
使用字典来记录
(3)使用回溯法,那么终止条件是什么
遍历到终点站结束,即该机场没有下一站
(4)搜索过程中,怎么遍历一个机场所对应的所有机场
用字典统计一个机场的所有航班信息,然后走完一个航班就删掉对应的航班信息,从而实现无重复的选择
class Solution(object):
def findItinerary(self, tickets):
"""
:type tickets: List[List[str]]
:rtype: List[str]
"""
self.adj = {}
#根据航班每一站的终点字母排序
tickets.sort(key=lambda x:x[1])
#罗列每一站的下一个可选项
for u, v in tickets:
if u in self.adj:
self.adj[u].append(v)
else:
self.adj[u] = [v]
#从JFK出发
self.res = []
self.dfs("JFK")
return self.res[::-1]
def dfs(self, s):
#出发城市有航班且能去到另一个地方
#终止条件:到达终点,此站没有下一站
while s in self.adj and len(self.adj[s]) > 0:
#找s能去哪里
v = self.adj[s][0]
#弹出避免死循环
self.adj[s].pop(0)
#递归
self.dfs(v)
#记录终点站,是倒序
self.res.append(s)
class Solution(object):
def findItinerary(self, tickets):
"""
:type tickets: List[List[str]]
:rtype: List[str]
"""
#使用字典存储映射关系
targets = defaultdict(list)
for ticket in tickets:
targets[ticket[0]].append(ticket[1])
#对到达机场列表进行逆序排序
for key in targets:
targets[key].sort(reverse = True)
res = []
self.backtracking("JFK", targets, res)
return res[::-1]
def backtracking(self, airport, targets, res):
while targets[airport]:
#机场还有可达站
next_airport = targets[airport].pop()
#递归
self.backtracking(next_airport, targets, res)
res.append(airport)
5.51. N皇后
题目链接:51. N皇后
文档讲解: 代码随想录

递归的思路:终止条件,只要搜索到树的叶子节点,就说明找到了皇后的位置。单层逻辑,递归深度由 row 来控制,即棋盘的行, for循环中 col 是棋盘的列,一行一列确定皇后的位置,判断此时棋盘是否合法,若合法则进一步递归。
判断棋盘是否合理:输入参数为,行数row,列数 col,此时棋盘
(1)判断同一列:检查棋盘前 row 列是否有皇后
(2)不用判断同一行是否有皇后,因为每一层递归,只会选择 for 循环中的一个元素,也就是每行只选一个位置来放置皇后
(3)斜角分为两个角度,45°和135°
class Solution(object):
def solveNQueens(self, n):
"""
:type n: int
:rtype: List[List[str]]
"""
res = []
chessboard = ['.' * n for i in range(n)]
self.backtracking(n, 0, res, chessboard)
return [[''.join(row) for row in re] for re in res] #res
def backtracking(self, n, row, res, chessboard):
#终止条件
if row == n:
res.append(chessboard[:])
return
for col in range(n):
if self.jiancha(row, col, chessboard):
#该位置合法
#放置皇后
chessboard[row] = chessboard[row][:col] + 'Q' + chessboard[row][col + 1:]
#下一行递归
self.backtracking(n, row + 1, res, chessboard)
#回溯
chessboard[row] = chessboard[row][:col] + '.' + chessboard[row][col + 1:]
def jiancha(self, row, col, chessboard):
#检查每列
for i in range(row):
if chessboard[i][col] == 'Q':
return False
#检查45°
i = row - 1
j = col - 1
while i >= 0 and j >= 0:
if chessboard[i][j] == 'Q':
return False
i -= 1
j -= 1
#检查135°
i = row - 1
j = col + 1
while i >= 0 and j < len(chessboard):
if chessboard[i][j] == 'Q':
return False
i -= 1
j += 1
return True
6.37. 解数独
题目链接:37. 解数独
文档讲解: 代码随想录
思路和N皇后差不多,但需要两层 for 循环来确定需要填入数字的位置。判断棋盘是否合法有三个维度,同行是否重复、同列是否重复、9宫格是否重复。
class Solution(object):
def solveSudoku(self, board):
"""
:type board: List[List[str]]
:rtype: None Do not return anything, modify board in-place instead.
"""
self.backtracking(board)
def backtracking(self, board):
#若有解,返回True
for i in range(len(board)):
for j in range(len(board[0])):
if board[i][j] != '.':
continue
for k in range(1, 10):
if self.jiancha(board, i, j, k):
#合法
board[i][j] = str(k)
if self.backtracking(board):
return True
board[i][j] ='.'
return False
return True
def jiancha(self, board, row, col, val):
#同行是否有重复
for i in range(9):
if board[row][i] == str(val):
return False
#同列
for i in range(9):
if board[i][col] == str(val):
return False
#九宫格
startrow = (row // 3) * 3
startcol = (col // 3) * 3
for i in range(startrow, startrow + 3):
for j in range(startcol, startcol + 3):
if board[i][j] == str(val):
return False
return True