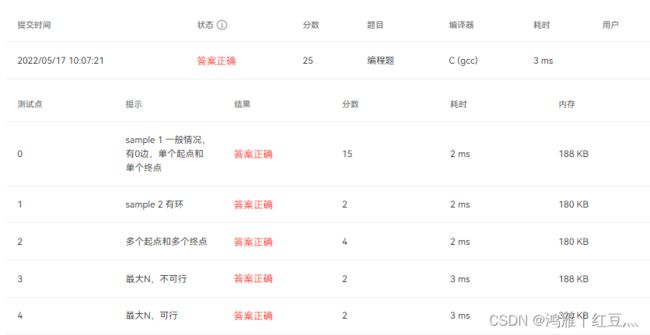
MOOC 数据结构 08-图8 How Long Does It Take——C语言

Given the relations of all the activities of a project, you are supposed to find the earliest completion time of the project.

Input Specification:

Each input file contains one test case. Each case starts with a line containing two positive integers N (≤100), the number of activity check points (hence it is assumed that the check points are numbered from 0 to N−1), and M, the number of activities. Then M lines follow, each gives the description of an activity. For the i-th activity, three non-negative numbers are given: S[i], E[i], and L[i], where S[i] is the index of the starting check point, E[i] of the ending check point, and L[i] the lasting time of the activity. The numbers in a line are separated by a space.

Output Specification:

For each test case, if the scheduling is possible, print in a line its earliest completion time; or simply output "Impossible".

Sample Input 1:

9 12
0 1 6
0 2 4
0 3 5
1 4 1
2 4 1
3 5 2
5 4 0
4 6 9
4 7 7
5 7 4
6 8 2
7 8 4

Sample Output 1:

18

Sample Input 2:

4 5
0 1 1
0 2 2
2 1 3
1 3 4
3 2 5

Sample Output 2:

Impossible

思路和小结： 

        这是一道考察有向无环图DAG(Directed Acyclic Graph)的题，是一道基础的拓扑排序题。

我们可以稍微拓展下：如何确定是否无环，即从任一顶点出发遍历图，都不会回到该顶点；所以判断是否是DAG时，有两种方法，即BFS和DFS；

        BFS方法就是老师讲的拓扑排序：有合理的拓扑序的图一定是无环图。

        DFS方法就是在DFS一条路径时，不会回到该路径上的任何一个顶点；

下面就这两种方法分别解题：

1.拓扑排序(变种的BFS)：增加一个数组，记录每个顶点的入度；将入度为0的顶点入队，开始BFS，每遍历一个顶点，它的邻接点入度-1，当入度为0时顶点入队；BFS完成后遍历了每个顶点，则是无环图；否则有环；

#include 
#include 
#include 

typedef int Vertex; //顶点
typedef int WeightType; //边权

typedef struct _Edge{ //边
	Vertex V1,V2;
	WeightType Weight;
}Edge;

typedef struct _Adj Adj; //邻接点
struct _Adj{
	Vertex AdjV;
	WeightType weight;
	Adj* Next;
};

typedef struct _LGraph{ //邻接表表示的图
	int Nv;
	int Ne;
	Adj** G;
}LGraph;

typedef struct _Queue{ //TopSort用到的队列
	Vertex* Data;
	int front;
	int rear;
}Queue;

LGraph* BuildGraph();

void InsertEdge( LGraph* Graph,Edge E );

void EarliestCompletionTime( LGraph* Graph );

bool TopSort( LGraph* Graph,int time[] );

void InitializeIndegree( LGraph* Graph,int Indegree[],int Len );

Queue* CreateQ( int N );

void AddQ( Queue* Q,Vertex V );

bool IsEmpty( Queue* Q );

Vertex DeleteQ( Queue* Q );

int Max( int time[],int N );

int main()
{
	LGraph* Graph = BuildGraph();
	
	EarliestCompletionTime( Graph );
	
	return 0;
}
//建图
LGraph* BuildGraph()
{
	LGraph* Graph = (LGraph*)malloc(sizeof(LGraph));
	
	scanf("%d %d",&Graph->Nv,&Graph->Ne);
	Graph->G = malloc(Graph->Nv*sizeof(Adj*));
	
	Vertex V;
	for(V=0;VNv;V++){
		
		Graph->G[V] = NULL;
	}
	
	Edge E;
	int i;
	for(i=0;iNe;i++){
		
		scanf("%d %d %d",&E.V1,&E.V2,&E.Weight);
		
		InsertEdge( Graph,E );
	}
	
	return Graph;
}

void InsertEdge( LGraph* Graph,Edge E )
{
	Adj* NewNode = (Adj*)malloc(sizeof(Adj));
	
	NewNode->AdjV = E.V2;
	NewNode->weight = E.Weight;
	NewNode->Next = Graph->G[E.V1];
	Graph->G[E.V1] = NewNode;
}
//解题
void EarliestCompletionTime( LGraph* Graph )
{
	int time[Graph->Nv]; //记录各个顶点最早完成时间
	
	Vertex V;           //time初始化
	for(V=0;VNv;V++){
		
		time[V] = 0;
	}
	
	bool IsDAG = TopSort( Graph,time ); //拓扑排序得出是否是DAG，并计算各顶点的time值
	
	if(IsDAG){
		
		printf("%d\n",Max( time,Graph->Nv));
	}else{
		
		printf("Impossible\n");
	}
}
//拓扑排序，同时计算time
bool TopSort( LGraph* Graph,int time[] )
{
	int Indegree[Graph->Nv]; //各个顶点的入度值
	InitializeIndegree( Graph,Indegree,Graph->Nv );
	
	Queue* Q = CreateQ(Graph->Nv);
	
	Vertex V;
	for(V=0;VNv;V++){
		
		if(Indegree[V] == 0){
			
			AddQ( Q,V );
		}
	}
	
	int cnt = 0; //计数器，记录已排序的顶点个数
	Adj* p; //临时指针
	while(!IsEmpty( Q )){
		
		V = DeleteQ( Q );
		cnt++;
		
		for(p=Graph->G[V];p;p=p->Next){ //V的每个邻接点
			
			Indegree[p->AdjV]--;
			
			if(Indegree[p->AdjV] == 0){
				
				AddQ( Q,p->AdjV );
			}
			
			if(time[V] + p->weight > time[p->AdjV]){ //更新time值
				
				time[p->AdjV] = time[V] + p->weight;
			}
		}
	}
	
	bool IsDAG = true; //判断是否是DAG
	if(cnt != Graph->Nv){
		
		IsDAG = false;
	}
	
	return IsDAG;
}

void InitializeIndegree( LGraph* Graph,int Indegree[],int Len )
{
	Vertex V;
	for(V=0;VG[V];p;p=p->Next){
			
			Indegree[p->AdjV]++;
		}
	}
}
//队列相关操作集
Queue* CreateQ( int N )
{
	Queue* Q = (Queue*)malloc(sizeof(Queue));
	
	Q->Data = malloc(N*sizeof(int));
	Q->front = Q->rear = -1;
	
	return Q;
}

void AddQ( Queue* Q,Vertex V )
{
	Q->rear++;
	Q->Data[Q->rear] = V;
}

bool IsEmpty( Queue* Q )
{
	return Q->front == Q->rear?true:false;
}

Vertex DeleteQ( Queue* Q )
{
	Q->front++;

	return Q->Data[Q->front];
}
//求最早完成时间
int Max( int time[],int N )
{
	int i,EariestCompletionTime = time[N-1];
	
	for(i=0;i EariestCompletionTime){
			
			EariestCompletionTime = time[i];
		}
	}
	
	return EariestCompletionTime;
}

 2.DFS：增加一个数组visited[ ]，确保每个顶点都遍历到；在深度遍历某一条具体路径时，如果又回到了该路径的上任一顶点，那么必定有环，所以增加一个数组collected[ ]，标记DFS时某一条路径上的每个顶点，递归到这条路径的终点时，表示无环，初始化这个数组，然后继续深度遍历下一条路径；

  

#include 
#include 
#include 

typedef int Vertex;
typedef int WeightType;

typedef struct _Edge{
	Vertex V1,V2;
	WeightType Weight;
}Edge;

typedef struct _Adj Adj;
struct _Adj{
	Vertex AdjV;
	WeightType weight;
	Adj* Next;
};

typedef struct _LGraph{
	int Nv;
	int Ne;
	Adj** G;
}LGraph;

LGraph* BuildGraph();

void InsertEdge( LGraph* Graph,Edge E );

void EarliestCompletionTime( LGraph* Graph );

bool DFS( LGraph* Graph,Vertex X,int time[],bool visited[],bool collected[] );

int Max( int time[],int N );

int main()
{
	LGraph* Graph = BuildGraph();
	
	EarliestCompletionTime( Graph );
	
	return 0;
}
//建图
LGraph* BuildGraph()
{
	LGraph* Graph = (LGraph*)malloc(sizeof(LGraph));
	
	scanf("%d %d",&Graph->Nv,&Graph->Ne);
	Graph->G = malloc(Graph->Nv*sizeof(Adj*));
	
	Vertex V;
	for(V=0;VNv;V++){
		
		Graph->G[V] = NULL;
	}
	
	Edge E;
	int i;
	for(i=0;iNe;i++){
		
		scanf("%d %d %d",&E.V1,&E.V2,&E.Weight);
		
		InsertEdge( Graph,E );
	}
	
	return Graph;
}

void InsertEdge( LGraph* Graph,Edge E )
{
	Adj* NewNode = (Adj*)malloc(sizeof(Adj));
	
	NewNode->AdjV = E.V2;
	NewNode->weight = E.Weight;
	NewNode->Next = Graph->G[E.V1];
	Graph->G[E.V1] = NewNode;
}

void EarliestCompletionTime( LGraph* Graph )
{
	int time[Graph->Nv];
	bool visited[Graph->Nv]; 
	bool collected[Graph->Nv];
	Vertex V;
	for(V=0;VNv;V++){
		
		time[V] = 0;
		visited[V] = false;
		collected[V] = false;
	}
	
	bool IsDAG = true;
	for(V=0;VNv;V++){ //确保有多个起点(入度为0)时,不会遗漏任何一个
		
		if(!visited[V] && IsDAG){
			
			IsDAG = DFS( Graph,V,time,visited,collected );
		}
	}
	
	if(IsDAG){
		
		printf("%d\n",Max( time,Graph->Nv));
	}else{
		
		printf("Impossible\n");
	}
	
}

bool DFS( LGraph* Graph,Vertex X,int time[],bool visited[],bool collected[] )
{
	bool IsDAG = true;
	
	visited[X] = true;
	
	if(Graph->G[X] == NULL){
		//递归到某条路径的终点时，初始化collected；
		Vertex V;
		for(V=0;VNv;V++){
			
			collected[V] = false;
		}
		
		return true;
	}
	
	Adj* p;
	for(p=Graph->G[X];p;p=p->Next){
		
		collected[X] = true; //某条路径开始的起点，标记一下
		
		if(IsDAG == false){  //如果已经发现有环，退出递归；
			
			return false;
		}
		
		if(collected[p->AdjV] == true){

			IsDAG = false;
			break;
		}else{
		
			if(time[X] + p->weight > time[p->AdjV]){
		
				time[p->AdjV] = time[X] + p->weight;
			}	
	
			IsDAG = DFS( Graph,p->AdjV,time,visited,collected );
		}	
	}
	
	return IsDAG;
}

int Max( int time[],int N )
{
	int i,EariestCompletionTime = time[N-1];
	
	for(i=0;i EariestCompletionTime){
			
			EariestCompletionTime = time[i];
		}
	}
	
	return EariestCompletionTime;
}

可以参考我写的判断DAG的方法的文章

数据结构 拓扑排序拓展 如何判断DAG_鸿雁丨红豆灬的博客-CSDN博客有向无环图 DAG(Directed Acyclic Graph)在学习拓扑排序的时候，我们知道如果一个有向图存在合理的拓扑序，那么这个图一定是DAG；以下是拓扑排序的伪码描叙：伪码描叙: void TopSort(){for(图中的每一个顶点V){ if(Indegree[V]==0){ AddQ( Q,V )；}}while(IsEmpty( Q )){V = DeleteQ( Q );输出V,或者记录V的输出序号;cnt++;for(V 的https://blog.csdn.net/h465705089/article/details/124818968