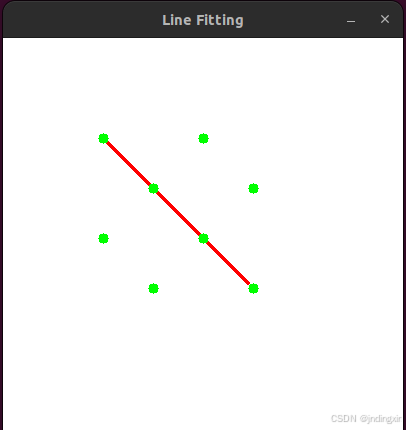
OpenCV结构分析与形状描述符(14)拟合直线函数fitLine()的使用
- 操作系统:ubuntu22.04
- OpenCV版本:OpenCV4.9
- IDE:Visual Studio Code
- 编程语言:C++11
算法描述
拟合一条直线到2D或3D点集。
fitLine 函数通过最小化 ∑ i ρ ( r i ) \sum_i \rho(r_i) ∑iρ(ri)来拟合一条直线到2D或3D点集,其中 r i r_i ri 是第i 个点到直线的距离,而 ρ ( r ) \rho(r) ρ(r)是一个距离函数,可以是以下之一:
-
DIST_L2
ρ ( r ) = r 2 / 2 (the simplest and the fastest least-squares method) \rho (r) = r^2/2 \quad \text{(the simplest and the fastest least-squares method)} ρ(r)=r2/2(the simplest and the fastest least-squares method) -
DIST_L1
ρ ( r ) = r \rho (r) = r ρ(r)=r -
DIST_L12
ρ ( r ) = 2 ⋅ ( 1 + r 2 2 − 1 ) \rho (r) = 2 \cdot ( \sqrt{1 + \frac{r^2}{2}} - 1) ρ(r)=2⋅(1+2r2−1) -
DIST_FAIR
ρ ( r ) = C 2 ⋅ ( r C − log ( 1 + r C ) ) where C = 1.3998 \rho \left (r \right ) = C^2 \cdot \left ( \frac{r}{C} - \log{\left(1 + \frac{r}{C}\right)} \right ) \quad \text{where} \quad C=1.3998 ρ(r)=C2⋅(Cr−log(1+Cr))whereC=1.3998 -
DIST_WELSCH
ρ ( r ) = C 2 2 ⋅ ( 1 − exp ( − ( r C ) 2 ) ) where C = 2.9846 \rho \left (r \right ) = \frac{C^2}{2} \cdot \left ( 1 - \exp{\left(-\left(\frac{r}{C}\right)^2\right)} \right ) \quad \text{where} \quad C=2.9846 ρ(r)=2C2⋅(1−exp(−(Cr)2))whereC=2.9846 -
DIST_HUBER
ρ ( r ) = { r 2 2 if r < C C ⋅ ( r − C 2 ) otherwise 此处 C = 1.345 \rho(r) = \begin{cases} \frac{r^2}{2} & \text{if } r < C \\ C \cdot (r - \frac{C}{2}) & \text{otherwise} \end{cases} 此处C=1.345 ρ(r)={2r2C⋅(r−2C)if r<Cotherwise此处C=1.345
该算法基于 M-估计器技术(http://en.wikipedia.org/wiki/M-estimator),该技术迭代地使用加权最小二乘法来拟合直线。在每次迭代之后,权重 w i w_i wi被调整为与 ρ ( r i ) \rho(r_i) ρ(ri)成反比。
函数原型
void cv::fitLine
(
InputArray points,
OutputArray line,
int distType,
double param,
double reps,
double aeps
)
参数
- 参数points 输入的2D或3D点集,存储在 std::vector<> 或 Mat 中。
- 参数输出的直线参数。在2D拟合的情况下,它应该是一个包含4个元素的向量(如 Vec4f)—— (vx, vy, x0, y0),其中 (vx, vy) 是与直线共线的归一化向量,(x0, y0) 是直线上的一点。在3D拟合的情况下,它应该是一个包含6个元素的向量(如 Vec6f)—— (vx, vy, vz, x0, y0, z0),其中 (vx, vy, vz) 是与直线共线的归一化向量,(x0, y0, z0) 是直线上的一点。
- 参数distType 由 M-估计器使用的距离类型,参见 DistanceTypes。
- 参数param 对某些类型的距离来说的数值参数(C)。如果它是0,则会选择一个最优值。
- 参数reps 对半径(坐标原点与直线之间的距离)的充分精度。
- 参数aeps 对角度的充分精度。对于 reps 和 aeps,0.01 是一个好的默认值。
代码示例
#include