VLSI电路单元的自动布局:全局布局基础介绍
2024年华数杯全国大学生数学建模竞赛B题为:VLSI电路单元的自动布局。本题主要关注的是全局布局问题。学术界针对全局布局的评估模型和优化方法的研究历史悠久。本文借题顺势介绍全局布局的一些重点基础内容和相关工具/资料,以期为对EDA算法设计领域感兴趣、对数学建模感兴趣的人降低研究门槛。
VLSI是超大规模集成电路的简称。完成一个VLSI设计的流程十分复杂,包含多种数据格式的转化,其中将逻辑网表转变为可制造的几何版图的过程称为物理设计。物理设计流程可以分为布图规划、布局(placement)、时钟树综合、布线等,其中布局由于决定了电路单元的位置进而会影响后续的阶段而显得尤为关键。
VLSI自动布局的目标是在芯片版图内确定所有电路单元的位置,使得总线长等一些指标最小,同时满足一些设计约束例如单元之间不重叠。由于布局是NP-hard问题,往往无法一步到位解决,因此常拆解为全局布局(global placement)、合法化(legalization)和详细布局(detailed placement)三个阶段求解。全局布局对单元不重叠视为软约束,根据总线长最小等目标确定电路单元的大致位置,布局结果允许单元重叠。合法化在尽量保持全局布局的结果下消除单元重叠,并让单元上下边界对齐行,左边界对齐网格边。详细布局进一步微调合法化的结果,例如局部交换单元位置,以寻求更好的指标结果。由于合法化和详细布局依赖于全局布局的解,因此全局布局至关重要,也是布局中最为关键且耗时的一个环节。
本文围绕全局布局关心的一些指标,对其评估模型和优化方法进行概述,最后介绍较有代表性的开源工具,并整理了一些可供学习的资料。
评估模型
全局布局阶段关心的指标主要有线长、密度、拥塞、时序等,其中线长和密度是最为基础且重要的,优化线长且满足密度约束的全局布局称为线长驱动的全局布局(wirelength-driven global placement)。本节主要介绍线长和密度的评估模型。
线长(Wirelength)
电路单元的位置主要根据单元之间的连接关系来确定。连接关系在布局阶段是一种逻辑概念,到后续布线阶段由于进行了实际的走线才由逻辑概念变成物理概念。在物理设计中,用“网表”来形容电路单元之间所有的连接关系,而用“线网”来形容其中的一组连接关系,即网表包含许多个线网。
已知电路单元之间的连接关系,目前主要采用连线长度(线长)来度量布局质量。一种直觉是,具有连接关系的几个电路单元应该摆放在一起,从而减少布线长度而减少所需布线资源,从而缩短信号传播时间而提高芯片性能。由于一个网表存在多组线网,通过总线长这项指标可以综合度量布局结果。总线长是全局布局中最常用最重要的优化目标,对每组线网算得线长后加和即为总线长,因此关键是计算每组线网的线长。
然而布局阶段的连接关系仅是一种逻辑概念,单元之间尚未实际布线,因此需要对线网长度进行预估。布局阶段最为准确的线长模型是RSMT(Rectilinear Steiner Minimal Tree),RSMT的值等于通过插入斯坦纳点构建的线段长度之和,但是构建RSMT是NP-hard问题,因此不常用于布局迭代优化中。最常用的线长评估模型是半周长线长HPWL(Half-Perimeter Wirelength),其数学表示如下:
H P W L ( x , y ) = max x − min x + max y − min y HPWL(x,y) = \max x - \min x + \max y - \min y HPWL(x,y)=maxx−minx+maxy−miny
其中 x , y x,y x,y分别表示线网中单元引脚(pin)的 x x x和 y y y坐标值。
HPWL计算简单,但是其无法对大于等于4pin的多pin线网进行准确的线长估计。据统计,尽管2pin和3pin的线网个数一般占比大于70%,但是其贡献的总线长却可能不高于50%。因此对多pin线网的线长进行高效准确的估计仍然是值得研究的问题。一项具有代表性的工作是FLUTE[1],其通过构建的查找表,可以对9pin以内线网进行快速准确的RSMT估计。
密度(Density)
单元密度是布局算法中主要的约束项。一方面,全局布局阶段通过权衡好线长减少和密度增加的关系来考虑可布线性。单元摆放越紧凑,线长越短,然而可能造成单元过于拥挤,单元引脚之间的布线空间遭到削减,从而损害可布线性。单元摆放也不能过于松散,这将带来线长的增加,消耗更多的布线资源,进一步损害可布线性。另一方面,在全局布局阶段分散单元,减小单元重叠,也可为后续合法化和详细布局阶段减轻优化的压力,进一步提高布局算法的整体执行效率。
在全局布局中,通常将布局区域划分为若干个相同大小的矩形网格,通过限制每个网格内单元密度的最大值来考虑密度约束。对于每个网格的单元密度,其数学表示如下:
D b ( x , y ) = ∑ v ∈ V P x ( b , v ) P y ( b , v ) D_{b}(x,y) = \sum_{v\in V} P_x(b,v)P_y(b,v) Db(x,y)=v∈V∑Px(b,v)Py(b,v)
其中, b b b表示每个网格, v v v表示任意的电路单元, P x P_x Px和 P y P_y Py分别表示单元 v v v和网格 v v v重叠的水平和竖直长度。对于限制每个网格内允许单元摆放的最大面积,其数学表示如下:
D b ( x , y ) ≤ ρ t A b D_{b}(x,y) \leq \rho_t A_b Db(x,y)≤ρtAb
其中, ρ t \rho_t ρt表示网格密度阈值(取值不大于1), A b A_b Ab表示每个网格的面积。
为计算网格的单元密度 D b ( x , y ) D_b(x,y) Db(x,y),重点是对网格和单元之间的重叠关系进行数学表示。文献[2]描述了两个模块之间的重叠函数。假设两个模块的左右边界分别为 [ L 1 , R 1 ] [L1,R1] [L1,R1]和 [ L 2 , R 2 ] [L2,R2] [L2,R2],则模块之间的水平重叠值可以表示为
f ( [ L 1 , R 1 ] , [ L 2 , R 2 ] ) = ∣ min ( R 1 , R 2 ) − max ( L 1 , L 2 ) ∣ + f([L1,R1],[L2,R2]) = |\min (R1,R2) - \max (L1,L2) |^{+} f([L1,R1],[L2,R2])=∣min(R1,R2)−max(L1,L2)∣+
其中,
[ z ] + = { z if z > 0 0 if z ≤ 0 [z]^{+}= \begin{cases}z & \text { if } z>0 \\ 0 & \text { if } z \leq 0\end{cases} [z]+={z0 if z>0 if z≤0
同理可以表示出模块之间的竖直重叠值。假设两个模块分别记为 i , j i,j i,j,模块的中心坐标记为 ( x , y ) (x,y) (x,y),模块的宽高记为 ( w , h ) (w,h) (w,h),则两个模块之间的重叠面积最终可以表示为
Overlap i j ( x i , y i , x j , y j ) = f ( [ x i − ω i 2 , x i + ω i 2 ] , [ x j − ω j 2 , x j + ω j 2 ] ) f ( [ y i − h i 2 , y i + b i 2 ] , [ y j − h j 2 , y j + h j 2 ] ) \begin{aligned} \operatorname{Overlap}_{i j}\left(x_i, y_i, x_j, y_j\right) & =f\left(\left[x_i-\frac{\omega_i}{2}, x_i+\frac{\omega_i}{2}\right],\left[x_j-\frac{\omega_j}{2}, x_j+\frac{\omega_j}{2}\right]\right) \\ & f\left(\left[y_i-\frac{h_i}{2}, y_i+\frac{b_i}{2}\right],\left[y_j-\frac{h_j}{2}, y_j+\frac{h_j}{2}\right]\right) \end{aligned} Overlapij(xi,yi,xj,yj)=f([xi−2ωi,xi+2ωi],[xj−2ωj,xj+2ωj])f([yi−2hi,yi+2bi],[yj−2hj,yj+2hj])
优化方法
文献[2]介绍了全局布局的三类经典算法:基于划分的方法、模拟退火算法、解析法。文献[3]系统梳理了应用解析法求解全局布局的常见优化模型与算法。本节将简单介绍目前学术界的SOTA(state-of-the-art)方案,即解析法中的非线性优化方法,基本元素包括线长光滑、密度光滑、梯度优化。
线长光滑
通常来说,全局布局的优化目标是最小化总线长。单个线网的评估模型常选用的是HPWL模型。然而HPWL不可微,为了能应用非线性优化的梯度求解,需要对HPWL模型进行近似光滑。常选用的线长光滑模型是 Weighted-Average(WA)[4]和Log-Sum-Ex(LSE)[5],其数学表示分别如下:
W W A ( e ) = ( ∑ i ∈ e x i exp ( x i / γ ) ∑ i ∈ e exp ( x i / γ ) − ∑ i ∈ e x i exp ( − x i / γ ) ∑ i ∈ e exp ( − x i / γ ) ) W_{WA}(\mathbf{{e}})=\left(\frac{\sum_{i \in e} x_{i} \exp \left(x_{i} / \gamma\right)}{\sum_{i \in e} \exp \left(x_{i} / \gamma\right)}-\frac{\sum_{i \in e} x_{i} \exp \left(-x_{i} / \gamma\right)}{\sum_{i \in e} \exp \left(-x_{i} / \gamma\right)}\right) WWA(e)=(∑i∈eexp(xi/γ)∑i∈exiexp(xi/γ)−∑i∈eexp(−xi/γ)∑i∈exiexp(−xi/γ))
W L S E ( e ) = γ ( ln ∑ i ∈ e exp ( x i γ ) + ln ∑ i ∈ e exp ( − x i γ ) ) W_{LSE}(\mathbf{{e}})=\gamma\left(\ln \sum_{i \in e} \exp \left(\frac{x_{i}}{\gamma}\right)+\ln \sum_{i \in e} \exp \left(\frac{-x_{i}}{\gamma}\right)\right) WLSE(e)=γ(lni∈e∑exp(γxi)+lni∈e∑exp(γ−xi))
其中, γ \gamma γ是光滑系数,用于控制线长模型的精度。 γ \gamma γ越大,线长模型越光滑但越不逼近HPWL。假设线网有2pin,坐标分别为 ( 0 , 0 ) (0,0) (0,0)和 ( x , 0 ) (x,0) (x,0),这里给出水平方向的线长光滑模型可视化(竖直方向同理)。
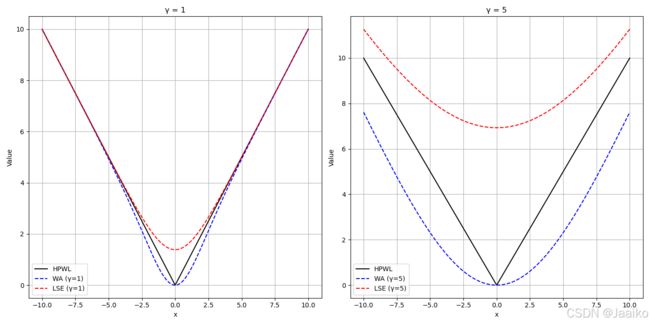
密度光滑
全局布局中计算电路单元与网格重叠长度的函数 P x ( b , v ) P_x(b,v) Px(b,v)和 P y ( b , v ) P_y(b,v) Py(b,v)同样不可微。为了能应用非线性优化的梯度求解,同样需要对其进行近似光滑。经典的密度光滑模型是Bell-shape[6]和Sigmoid[7]。应用Bell-shape对 P x ( b , v ) P_x(b,v) Px(b,v)的光滑近似表示如下( P x ( b , v ) P_x(b,v) Px(b,v)同理):
p x ( b , v ) = { 1 − a d x 2 , 0 ≤ d x ≤ w v 2 + w b b ( d x − w v 2 − 2 w b ) 2 , w v 2 + w b ≤ d x ≤ w v 2 + 2 w b 0 , w v 2 + 2 w b ≤ d x p_x(b, v)= \begin{cases}1-a d_x^2, & 0 \leq d_x \leq \frac{w_v}{2}+w_b \\ b\left(d_x-\frac{w_v}{2}-2 w_b\right)^2, & \frac{w_v}{2}+w_b \leq d_x \leq \frac{w_v}{2}+2 w_b \\ 0, & \frac{w_v}{2}+2 w_b \leq d_x\end{cases} px(b,v)=⎩ ⎨ ⎧1−adx2,b(dx−2wv−2wb)2,0,0≤dx≤2wv+wb2wv+wb≤dx≤2wv+2wb2wv+2wb≤dx
其中, d x d_x dx是电路单元与网格的中心点水平距离, a a a和 b b b分别表示如下:
a = 4 ( w v + 2 w b ) ( w v + 4 w b ) b = 2 w b ( w v + 4 w b ) \begin{aligned} a & =\frac{4}{\left(w_v+2 w_b\right)\left(w_v+4 w_b\right)} \\ b & =\frac{2}{w_b\left(w_v+4 w_b\right)} \end{aligned} ab=(wv+2wb)(wv+4wb)4=wb(wv+4wb)2
假设网格宽度为 2 2 2,电路单元宽度为 1 1 1,对原始水平重叠函数 P x ( b , v ) P_x(b,v) Px(b,v)和应用Bell-shape、Sigmoid光滑后的函数进行可视化。可知,相比Bell-shape函数,Sigmoid光滑化可以给出更准确的近似。
梯度优化
光滑后的线长模型和密度模型随后通过拉格朗日罚方法或松弛整合为一个无约束的非线性优化函数,可表示如下:
min W ( x , y ) + λ ∑ b ( D b ( x , y ) − M b ) 2 \min \quad {W}(\mathbf{x}, \mathbf{y})+\lambda \sum_{b}\left({D}_{b}(\mathbf{x}, \mathbf{y})-M_{b}\right)^{2} minW(x,y)+λb∑(Db(x,y)−Mb)2
其中, W ( x , y ) {W}(\mathbf{x}, \mathbf{y}) W(x,y) 是光滑后的总线长, D b ( x , y ) D_{b}(\mathbf{x}, \mathbf{y}) Db(x,y)是光滑后的网格密度, M b = ρ t A b M_{b} = \rho_t A_b Mb=ρtAb 指每个网格内允许电路单元摆放的最大面积。随后,通过对该函数应用梯度优化算法即可求解出布局结果。
常用的梯度优化算法是Conjugate Gradient(CG)和Nesterov算法。CG算法在执行线搜索时较为耗时,其步长也不够精确,搜索方向在迭代过程中很容易失去共轭性,这些因素导致CG算法的性能较差。ePlace[8]首次利用 Nesterov 算法结合 Lipschitz 常数预测的方法,获得了比 CG 算法更好的布局质量和更短的求解时间。目前全局布局的主流梯度优化方法即是采用ePlace这套方法。
相关工具/资料
DREAMPlace
DREAMPlace[9]是目前学术界布局工具的SOTA解决方案。其特点是将非线性优化方法的求解过程类比为深度学习训练问题,进而可以使用深度学习工具包开发,以实现灵活性和效率。该工具在CPU和GPU上均可运行,采用GPU加速方案可以实现对布局的高效快速求解。DREAMPlace目前已迭代到4.0版本,支持线长驱动(1.0)、可布线性驱动(2.2.0)、时序驱动(4.0)等多种特性的全局布局方案。
代码仓库:https://github.com/limbo018/DREAMPlace.git
iEDA-iPL
iPL是iEDA[10]开源平台上的一款布局工具。作为iEDA的一部分,iPL从iEDA的数据库中读取数据到数据访问层,支持常见的工业标准文件,如.v、.DEF、.LEF、.lib等,并支持主要操作包括初始布局、全局布局、全局布局后、合法化、详细布局、缓冲插入、填充插入和检查器。它封装了常见的实用类,如日志、报告和实用程序,以及数学操作库和性能库,为用户提供了TCL、Python和C++的API。
iPL基于iEDA统一设计的数字后端全流程框架开发,代码实现规范,用户友好,同时便于基于iEDA平台实现各类功能扩展,十分具有潜力。目前iPL同样支持线长驱动、可布线性驱动、时序驱动等多种特性的全局布局方法。
代码仓库:https://gitee.com/oscc-project/iEDA.git
视频介绍:
- 【2024年EDA人才培养计划:布局最新介绍】 https://www.bilibili.com/video/BV1Yx4y147oP/?share_source=copy_web&vd_source=6815ab875317a5897f502233fc7d69c1
- 【iEDA-Tutorial-第二期:iEDA-iPL 问题介绍、架构、使用与规划】 https://www.bilibili.com/video/BV1GN411h7b3/?share_source=copy_web&vd_source=6815ab875317a5897f502233fc7d69c1
参考文献
[1] Chu, Chris. “FLUTE: Fast lookup table based wirelength estimation technique.” In IEEE/ACM International Conference on Computer Aided Design, 2004. ICCAD-2004., pp. 696-701. IEEE, 2004.
[2] Wang, Laung-Terng, Yao-Wen Chang, and Kwang-Ting Tim Cheng, eds. Electronic design automation: synthesis, verification, and test. Morgan Kaufmann, 2009.
[3] 黄志鹏, 李兴权, and 朱文兴. “超大规模集成电路布局的优化模型与算法.” 运筹学学报 25, no. 3 (2021): 15-36.
[4] Hsu, Meng-Kai, Yao-Wen Chang, and Valeriy Balabanov. “TSV-aware analytical placement for 3D IC designs.” In Proceedings of the 48th Design Automation Conference, pp. 664-669. 2011.
[5] Naylor, William C., Ross Donelly, and Lu Sha. “Non-linear optimization system and method for wire length and delay optimization for an automatic electric circuit placer.” U.S. Patent 6,301,693, issued October 9, 2001.
[6] Kahng, Andrew B., and Qinke Wang. “Implementation and extensibility of an analytic placer.” In Proceedings of the 2004 international symposium on Physical design, pp. 18-25. 2004.
[7] Chou, Sheng, Meng-Kai Hsu, and Yao-Wen Chang. “Structure-aware placement for datapath-intensive circuit designs.” In Proceedings of the 49th Annual Design Automation Conference, pp. 762-767. 2012.
[8] Lu, Jingwei, Pengwen Chen, Chin-Chih Chang, Lu Sha, Dennis Jen-Hsin Huang, Chin-Chi Teng, and Chung-Kuan Cheng. “ePlace: Electrostatics-based placement using fast fourier transform and Nesterov’s method.” ACM Transactions on Design Automation of Electronic Systems (TODAES) 20, no. 2 (2015): 1-34.
[9] Lin, Yibo, Shounak Dhar, Wuxi Li, Haoxing Ren, Brucek Khailany, and David Z. Pan. “Dreamplace: Deep learning toolkit-enabled gpu acceleration for modern vlsi placement.” In Proceedings of the 56th Annual Design Automation Conference 2019, pp. 1-6. 2019.
[10] Li X, Tao S, Huang Z, et al. ieda: An open-source intelligent physical implementation toolkit and library[J]. arXiv preprint arXiv:2308.01857, 2023.
