usaco chapter1:4,5 （1）

  1.4 packing rectangle

 刚看题目觉得无从下手，虽然只有4个矩形，但是组合的方法很多，最初的想法是bfs，每放一个矩形，就会产生新的边界......这样问题是非常，非常非常非常非常复杂的。

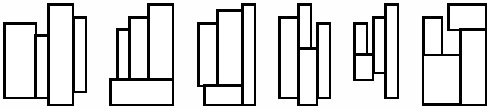
 不过仔细再读题目，题头的那个被我忽略的图片才是解题关键，它告诉我们只有这6种摆法，其实仔细分析，第4，5种是同一种。

 每种摆法都可以模拟（前面几种比较简单，第6种貌似要复杂一点），我的想法是：

第1种，按次序摆放；

 2 ，分层摆放，先放下层（要枚举），再放上层，每一层有一个broad,总共有一个high，broad取最大的；

 3 ，分层，先枚举放下层，再枚举放右的，最后放左侧的2个，这种方案要计算上下层的broad 和左右的high；

 4、5 ，先放中间的2个（要枚举，上下层）再放左右的2个， 有上下2层的broad，中和两侧的high要计算，依然取最大值；

6   网上对这个的摆放讨论很多，为了避免矩形重叠，进行了复杂的讨论，不过我感觉只要按顺序来摆放就OK了，

 举个例子，如果右上角的矩形很宽，就想象它把左边的矩形挤开了，就算被挤出了下层矩形的宽度，依然不会掉下来而是挨着它右边的，

   于是我们每放一块，都要统计此时上下层的broad和左右的high。

 

经过上面分析，代码量是巨大的。

6种情况分别coding，将近400行了，第一次写这么长，颇为壮观......

#include<stdio.h>
#include<string.h>
typedef struct matrix
{
 int lon;
 int broad;
}matrix;
matrix rect[4];
char judge[10];

void f(int k)       //生成矩形摆放的组合情况；0表示横，1表示竖；
{
 int i=0;
 while(k!=0)
 {
  judge[i++]=k%2;
  k/=2;
 }
}

int max(int x,int y)
{
 if(x>y)return x;
 else
 return y;
}

int templ,tempb;

void cases1()
{
 int lon,broad,i,j;
 templ=tempb=100;
 for(i=0;i<16;i++)
 {
  lon=broad=0;
  memset(judge,0,sizeof(judge));
  f(i);
  for(j=0;j<4;j++)
  {
   if(!judge[j])
   {
    broad+=rect[j].broad;
    lon+=rect[j].lon;
   }
   else
   {
  //  upside(&rect[j])
    broad+=rect[j].lon;
    lon+=rect[j].broad;
   }
  }
   if(templ * tempb > lon * broad)
   {
    templ=lon;
    tempb=broad;
   }
 }
}

void cases2()
{
 int lon1,lon2,broad1,broad2,i,j,k,vis[4];
 templ=tempb=100;
 for(i=0;i<16;i++)
 {
  broad1=broad2=0;
  memset(judge,0,sizeof(judge));
  f(i);
  memset(vis,0,sizeof(vis));
  for(j=0;j<4;j++)     //先找一个放在最下面；
  {
   if(!judge[j])
   {
    broad1=rect[j].lon;
    lon1=rect[j].broad;
   }
   else
   {
    //upside(&rect[j]);
    broad1=rect[j].broad;
    lon1=rect[j].lon;
   }
   vis[j]=1;
   for(k=0,lon2=0;k<4;k++)
    if(!vis[k])
    {
     if(!judge[k])
     {
      broad2+=rect[k].broad;
      lon2=max(lon2,lon1+rect[k].lon);
     }
     else
     {
      broad2+=rect[k].lon;
      lon2=max(lon2,lon1+rect[k].broad);
     }
    }
    if(templ * tempb > max(broad2,broad1) * lon2)
     {
      templ=lon2;
      tempb=max(broad2,broad1);
     }
  }
 }
}
void cases3()
{
 int lon1,lon2,broad1,broad2,i,j,k,r;
 templ=tempb=100;
 for(i=0;i<16;i++)
 {
  broad1=broad2=0;
  memset(judge,0,sizeof(judge));
  f(i);
 // memset(vis,0,sizeof(vis));
  for(j=0;j<4;j++)      //放一个在最下面；
  {
   if(!judge[j])
   {
    broad1=rect[j].lon;
    lon1=rect[j].broad;
   }
   else
   {
    broad1=rect[j].broad;
    lon1=rect[j].lon;
   }
   
   for(k=0,lon2=0;k<4;k++)   //放一个在边上
   if(k!=j)
   {
    if(!judge[k])
    {
     broad1+=rect[k].broad;
     broad2=rect[k].broad;
     lon2=max(lon1,rect[k].lon);
    }
    else
    {
     broad1+=rect[k].lon;
     broad2+=rect[k].lon;
     lon2=max(lon1,rect[k].broad);
    }

    for(r=0;r<4;r++)    //计算另外2个生成的broad和lon
    if(r!=k&&r!=j)
    {
     if(!judge[r])
     {
      broad2+=rect[r].broad;
      lon1+=rect[r].lon;
     }
     else
     {
      broad2+=rect[r].lon;
      lon1+=rect[r].broad;
     }
    }
     if(templ * tempb> max(broad1,broad2) * max(lon1,lon2))
     {
      tempb=max(broad1,broad2);
      templ=max(lon1,lon2);
     }
   }
  } 
 }
}
void cases4()
{
 int lon1,lon2,broad1,i,j,k,r;
 templ=tempb=100;
 for(i=0;i<16;i++)
 {
  broad1=0;
  memset(judge,0,sizeof(judge));
  f(i);
 // memset(vis,0,sizeof(vis));
  for(j=0;j<4;j++)      //放一个在最下面；
  {
   if(!judge[j])
   {
    broad1=rect[j].broad;
    lon1=rect[j].lon;
   }
   else
   {
    broad1=rect[j].lon;
    lon1=rect[j].broad;
   }
   
   for(k=0,lon2=0;k<4;k++)    //向上添一层；
   if(k!=j)
   {
    if(!judge[k])
    {
     broad1=max(rect[k].broad,broad1);
     lon1+= rect[k].lon;
    // broad2=rect[k].broad;
    // lon2=lon2>rect[k].lon? lon2 : rect[k].lon;
    }
    else
    {
     broad1=max(rect[k].lon,broad1);
     lon1+=rect[k].broad;
    // broad2+=rect[k].lon;
    // lon2=lon2 >rect[k].broad? lon2 : rect[k].broad;
    }
    for(r=0;r<4;r++)
    if(r!=k&&r!=j)     //向两边添矩形块；
    {
     if(!judge[r])
     {
      broad1+=rect[r].broad;
      lon2=max(lon2,rect[r].lon);
     }
     if(judge[r])
     {
      broad1+=rect[r].lon;
      lon2=max(lon2,rect[r].lon);
     }
    }
     if(templ * tempb > broad1 * max(lon2,lon1))
     {
      templ=max(lon2,lon1);
      tempb=broad1;
     }
   } 
  }
 }
}
//int cases5()
void cases6()
{
 int i,j,k,r,s,lon1,lon2,broad1,broad2;
 templ=tempb=100;
 for(i=0;i<16;i++)
 {
  memset(judge,0,sizeof(judge));
  f(i);
  for(j=0;j<4;j++)    //先放一个矩形块；
  {
   if(judge[j]==0)
   {
    broad1=rect[j].broad;
    lon1=rect[j].lon;
   }
   if(judge[j]==1)
   {
    broad1=rect[j].lon;
    lon1=rect[j].broad;
   }
   for(k=0;k<4;k++)
   if(k!=j)     //放下层的第2个
   {
    if(judge[k]==0)
    {
     broad1+=rect[k].broad;
     lon2=rect[k].lon;
    }
    if(judge[k]==1)
    {
     broad1+=rect[k].lon;
     lon2=rect[k].broad;
    }
    for(r=0;r<4;r++)  //放上层第1个
    if(r!=j&&r!=k)
    {
     if(judge[r]==0)
     {
      broad2=rect[r].broad;
      lon1+=rect[r].lon;
     }
     if(judge[r]==1)
     {
      broad2=rect[r].lon;
      lon1+=rect[r].broad;
     }
     for(s=0;s<4;s++) //放上层第2个；
     if(s!=j&&s!=k&&s!=r)
     {
      if(judge[s]==0)
      {
       broad2+=rect[s].broad;
       lon2+=rect[s].lon;
      }
      if(judge[s]==1)
      {
       broad2+=rect[s].lon;
       lon2+=rect[s].broad;
      }
      if(templ * tempb > max(lon1,lon2) * max(broad1,broad2))
      {
       templ=max(lon1,lon2);
       tempb=max(broad1,broad2);
      }
     }
    }
   }
  }
 }
}

int main()
{
 int i,j=0,minl,minb,t,lon[6],broad[6];
 for(i=0;i<4;i++)
 {
  scanf("%d%d",&rect[i].lon,&rect[i].broad);
  if(rect[i].lon<rect[i].broad)
  {
   t=rect[i].lon;
   rect[i].lon=rect[i].broad;
   rect[i].broad=t;
  }
 }
 
 cases1();
 minl=templ;
 minb=tempb;
 lon[j]=templ;
 broad[j++]=tempb;

 cases2();
 if(templ * tempb < minl * minb)
 {
  minl=templ;
  minb=tempb;
 }
 lon[j]=templ;
 broad[j++]=tempb;

 cases3();
 if(templ * tempb < minl * minb)
 {
  minl=templ;
  minb=tempb;
 }
 lon[j]=templ;
 broad[j++]=tempb;

 cases4();
 if(templ * tempb < minl * minb)
 {
  minl=templ;
  minb=tempb;
 }
 lon[j]=templ;
 broad[j++]=tempb;

 cases6();
 if(templ * tempb < minl * minb)
 {
  minl=templ;
  minb=tempb;
 }
 lon[j]=templ;
 broad[j++]=tempb;

 for(i=0;i<j;i++)
  if(broad[i] * lon[i]==minl * minb)
  {
   printf("%d\n",minl*minb);
   if(broad[i]<=lon[i])
   printf("%d %d\n",broad[i],lon[i]);
   else
   printf("%d %d\n",lon[i],broad[i]);
  }

 return 0;
}

 

S形的性感代码......可惜没有AC....囧！！

 

 

 

偷懒nocow上抄一个算完了。

另外，要注意的是矩形的可以横放和竖放的， 所以还要枚举各种情况（真tm没完啊！！～～～）

      个矩形2种状态共4个可以用2进制来表示，将i从0到15枚举，转成2进制存入数组，当前元素为1横放，为0竖放.......       

本文使用Blog_Backup未注册版本导出，请到soft.pt42.com注册。