Flowerpot S
[USACO12MAR] Flowerpot S
Description
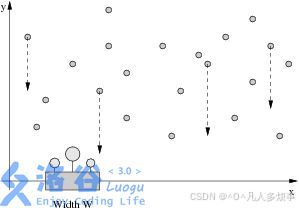
Farmer John has been having trouble making his plants grow, and needs your help to water them properly. You are given the locations of N raindrops (1 <= N <= 100,000) in the 2D plane, where y represents vertical height of the drop, and x represents its location over a 1D number line:
Each drop falls downward (towards the x axis) at a rate of 1 unit per second. You would like to place Farmer John’s flowerpot of width W somewhere along the x axis so that the difference in time between the first raindrop to hit the flowerpot and the last raindrop to hit the flowerpot is at least some amount D (so that the flowers in the pot receive plenty of water). A drop of water that lands just on the edge of the flowerpot counts as hitting the flowerpot.
Given the value of D and the locations of the N raindrops, please compute the minimum possible value of W.
老板需要你帮忙浇花。给出 N 滴水的坐标,y 表示水滴的高度,xx 表示它下落到 xx 轴的位置。
每滴水以每秒 11 个单位长度的速度下落。你需要把花盆放在 xx 轴上的某个位置,使得从被花盆接着的第 11 滴水开始,到被花盆接着的最后 11 滴水结束,之间的时间差至少为 DD。
我们认为,只要水滴落到 x 轴上,与花盆的边沿对齐,就认为被接住。给出 NN 滴水的坐标和 D 的大小,请算出最小的花盆的宽度 W。
Input
第一行 2 个整数 N 和 D。
接下来 N行每行 2 个整数,表示水滴的坐标 (x,y)。
Output
仅一行 1 个整数,表示最小的花盆的宽度。如果无法构造出足够宽的花盆,使得在 DD 单位的时间接住满足要求的水滴,则输出 −1。
Sample 1
| Inputcopy | Outputcopy |
|---|---|
4 5 6 3 2 4 4 10 12 15 |
2 |
Hint
有 4滴水,(6,3) ,(2,4) ,(4,10),(12,15)。水滴必须用至少 5 秒时间落入花盆。花盆的宽度为 2 是必须且足够的。把花盆放在 x=4…6的位置,它可以接到 1 和 3 水滴, 之间的时间差为 10−3=71 满足条件。
【数据范围】
40% 的数据:1≤N≤10001≤N≤1000 ,1≤D≤20001≤D≤2000 。
100% 的数据:1≤N≤1051≤N≤105 ,1≤D≤1061≤D≤106 ,0≤x,y≤1060≤x,y≤106 。
思路:
先将所有的数按照从小到大的顺序排列,然后用两个单调队列储存队首值max的单调递减和队首值min的单调递增数列,其数列存储下标。在变例过的数中两队首差最大,若差大于D,着存在,比较宽度。在看两队首的位置,哪个队首在左边,哪个队首就向后移一位,再比较(这样移动若成立宽度降低,若不成立,则继续遍历比较)。
若不移动这往后遍历,宽度会变大。
代码:
#define _CRT_SECURE_NO_WARNINGS
#include
struct s {
int x, y;
};
struct s a[100002],e[100002];
int b[100002], c[100002];//b存储max,单调减,c储存min,单调增
int n, d,min=9999999;
//归并排序从小到大
void digui(int i, int j) {
if (i >= j) {
return;
}
int mid = i + (j - i) / 2;
digui(i, mid);
digui(mid + 1, j);
int r = i, l = mid + 1, h = i;
while (r <= mid && l <= j) {
if (a[r].x < a[l].x) {
e[h].x = a[r].x;
e[h].y = a[r].y;
h++;
r++;
}
else {
e[h].x = a[l].x;
e[h].y = a[l].y;
h++;
l++;
}
}
while (r <= mid) {
e[h].x = a[r].x;
e[h].y = a[r].y;
h++;
r++;
}
while (l <= j) {
e[h].x = a[l].x;
e[h].y = a[l].y;
h++;
l++;
}
h = i;
while (h <= j) {
a[h].x = e[h].x;
a[h].y = e[h].y;
h++;
}
}
//取距离最小
void MIN(int l, int x) {
int k = a[b[l]].x - a[c[x]].x;
if (k < 0) {
k = 0-k;
}
min = min > k ? k : min;
}
int main() {
scanf("%d %d", &n, &d);
for (int i = 1;i <= n;i++) {
scanf("%d %d", &a[i].x, &a[i].y);
}
digui(1, n );
int l = 1, r = 0;
int x = 1, y = 0;
b[++r] = 1;//max下标
c[++y] = 1;//min下标
for (int i = 1;i < n;i++) {
//b中单调减
if (a[b[r]].y >= a[i].y) {
b[++r] = i;
}
else{
while(a[b[r]].y < a[i].y&&r>=l) {
--r;
}
b[++r] = i;
}
//c中单调增
if (a[c[y]].y <= a[i].y) {
c[++y] = i;
}
else {
while (a[c[y]].y > a[i].y && y >= x) {
--y;
}
c[++y] = i;
}
//判断b的队首最大,c的队首最小
while (a[b[l]].y - a[c[x]].y >= d&&l<=r&&x<=y) {
MIN(l, x);//取距离最小
if (a[b[l]].x < a[b[x]].x) {
l++;
}//若b队首在c队首左边,++l比较,若成立mi更小
else {
x++;
}//若b队首在c队首左边,++x比较,若成立min更小,
}
//防止队空
if (l > r) {
l--;
}
if (x > y) {
x--;
}
}
if (min == 9999999) {
printf("-1\n");
}
else {
printf("%d\n", min);
}
return 0;
}