*Next Permutation
题目:
Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such arrangement is not possible, it must rearrange it as the lowest possible order (ie, sorted in ascending order).
The replacement must be in-place, do not allocate extra memory.
Here are some examples. Inputs are in the left-hand column and its corresponding outputs are in the right-hand column.
1,2,3 → 1,3,2
3,2,1 → 1,2,3
1,1,5 → 1,5,1
解题思想:
对于数字序列:
先看前面2排的话,可以看出来第二排是比第一排要大的,参考字符串比较大小的问题。那么第2个排列是不是第一个排列的下一个排列呢。很明显不是,第3个排列才是, 那么如何获取到下一个排列呢。步骤比较简单:假设数组大小为 n
Supplement:
“这道题是给定一个数组和一个排列,求下一个排列。算法上其实没有什么特别的地方,主要的问题是经常不是一见到这个题就能马上理清思路。下面我们用一个例子来说明,比如排列是(2,3,6,5,4,1),求下一个排列的基本步骤是这样:
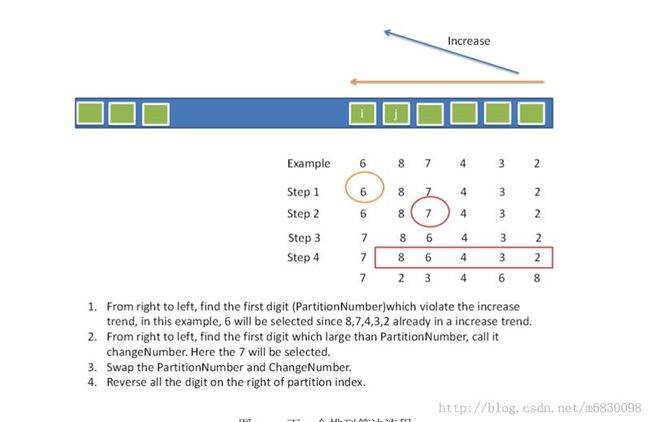
1) 先从后往前找到第一个不是依次增长的数,记录下位置p。比如例子中的3,对应的位置是1;
2) 接下来分两种情况:
(1) 如果上面的数字都是依次增长的,那么说明这是最后一个排列,下一个就是第一个,其实把所有数字反转过来即可(比如(6,5,4,3,2,1)下一个是(1,2,3,4,5,6));
(2) 否则,如果p存在,从p开始往后找,找找找,找到第一个比他bigger的数,然后两个调换位置,比如例子中的4。调换位置后得到(2,4,6,5,3,1)。最后把p之后的所有数字倒序,比如例子中得到(2,4,1,3,5,6), 这个即是要求的下一个排列。
以上方法中,最坏情况需要扫描数组三次,所以时间复杂度是O(3*n)=O(n),空间复杂度是O(1)。代码如下:”
1 public class Solution { 2 //http://blog.csdn.net/linhuanmars/article/details/20434115 3 /* 4 假设数组大小为 n 5 1.从后往前,找到第一个 A[i-1] < A[i]的。也就是第一个排列中的 6那个位置,可以看到A[i]到A[n-1]这些都是单调递减序列。 6 2.从 A[n-1]到A[i]中找到一个比A[i-1]大的值(也就是说在A[n-1]到A[i]的值中找到比A[i-1]大的集合中的最小的一个值) 7 3.交换 这两个值,并且把A[n-1]到A[i+1]排序,从小到大。 8 */ 9 public void nextPermutation(int[] num) { 10 if(num==null || num.length==0) 11 return; 12 int i = num.length-2; 13 while(i>=0 && num[i]>=num[i+1]) 14 i--; 15 16 if(i>=0){ 17 int j=i+1; 18 while(j<num.length && num[j]>num[i]) 19 j++; 20 j--; 21 swap(num,i,j); 22 } 23 reverse(num, i+1,num.length-1); 24 } 25 private void swap(int[] num, int i, int j){ 26 int tmp = num[i]; 27 num[i] = num[j]; 28 num[j] = tmp; 29 } 30 private void reverse(int[] num, int i, int j){ 31 while(i < j) 32 swap(num, i++, j--); 33 }
Reference:
http://www.cnblogs.com/springfor/p/3896245.html
http://fisherlei.blogspot.com/2012/12/leetcode-next-permutation.html
http://blog.csdn.net/m6830098/article/details/17291259