POJ 3321 Apple Tree (DFS + 树状数组)

题意：

一棵苹果树有N个分叉，编号1---N（根的编号为1），每个分叉只能有一颗苹果或者没有苹果。 现在有两种操作：

1.某个分叉上的苹果从有变无或者从无边有。

2.需要统计以某个分叉为根节点时，它的子树上（包括该分叉）共有多少苹果。

分析： 有两种操作，基本就是使用数据结构维护的题目了。开始想了很久，不懂如何将分叉转化为一维线性的树状数组维护。 看了下discuss，有人说了时间戳三字。想了想，发现如果按照节点遍历的顺序可以制造出时间上的线性关系。 例如：

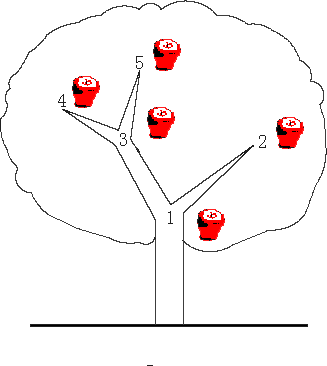
连接情况为：1---->2     1--->3    3--->4        3--->5

以1为根节点开始dfs，则遍历到每个点的时间可以为       1---->1     3--->2    4--->3    5---->4     2--->5

用两个数组begin，end统计以节点i为根时，遍历的第一个点的时间，和遍历最后一个点的时间

所以：begin[1] = 1 ;  end[1] = 5;   begin[2] = 5 ; end[2] = 5;   begin[3] = 2; end[3] = 4;........................................................

改变节点i的状态，时间戳小于i的会受影响；求和时，只需求(begin[i],end[i])的和了............................这样就变成了单点更新，区间求和的问题了。

 

#include <iostream>

#include <algorithm>

#include <cmath>

#include <cstdio>

#include <cstdlib>

#include <cstring>

#include <string>

#include <vector>

#include <set>

#include <queue>

#include <stack>

#include <climits>//形如INT_MAX一类的

#define MAX 100005

#define INF 0x7FFFFFFF

#define REP(i,s,t) for(int i=(s);i<=(t);++i)

#define ll long long

#define mem(a,b) memset(a,b,sizeof(a))

#define mp(a,b) make_pair(a,b)

#define L(x) x<<1

#define R(x) x<<1|1

# define eps 1e-5

//#pragma comment(linker, "/STACK:36777216") ///传说中的外挂

using namespace std;



int begin[MAX],end[MAX],cnt[MAX],vis[MAX];

int c[MAX];

int n,m,step;

char op;

struct node {

    int s,e,next;

} ed[MAX];

int head[MAX],num;



void init() {

    memset(head,-1,sizeof(head));

    num = 0;

    step = 1;

    memset(c,0,sizeof(c));

    memset(cnt,1,sizeof(cnt));

    memset(vis,0,sizeof(vis));

}



void addedge(int s,int e) {

    ed[num].s = s;

    ed[num].e = e;

    ed[num].next = head[s];

    head[s] = num ++;

}



int lowbit(int x) {

    return x & (-x);

}



void update(int x,int va) {

    while(x > 0) {

        c[x] += va;

        x -= lowbit(x);

    }

}



int query(int x) {

    int sum = 0;

    while(x <= n) {

        sum += c[x];

        x += lowbit(x);

    }

    return sum;

}



void dfs(int v0) {

    vis[v0] = 1;

    begin[v0] = step;

    for(int i=head[v0]; i != -1; i = ed[i].next) {

        int e = ed[i].e;

        if(vis[e] == 0) {

            step ++;

            dfs(e);

        }

    }

    end[v0] = step;

}



int main() {

    init();

    scanf("%d",&n);

    int x,y;

    for(int i=0; i<n-1; i++) {

        scanf("%d%d",&x,&y);

        addedge(x,y);

    }

    dfs(1);

    for(int i=1; i<=n; i++) update(i,1);

    scanf("%d",&m);

    for(int i=0; i<m; i++) {

        getchar();

        scanf("%c%d",&op,&x);

        if(op == 'Q') {

            printf("%d\n",query(begin[x]) - query(end[x] + 1));

        }

        if(op == 'C') {

            cnt[x] ++;

            if(cnt[x] % 2 == 0) update(begin[x],-1);

            else update(begin[x],1);

        }

    }

    return 0;

}