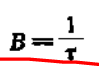傅立叶变换,时域,频域二
参考文献:
信号完整性分析
"信息传输调制和噪声"P31,
"傅立叶变换的数学再认识"及若干网上博客。
目录
信号分析方法概述
时域
频域
时域与频域的互相转换
傅立叶变换 原理
傅立叶变换 分类
傅立叶级数的五个公式(周期性函数)
傅立叶积分(非周期性函数)
振幅谱和相位谱的关系
功率谱
傅立叶变换推导出:时移原理与频移原理,对偶性质
时间-频率 间的对应关系。
对应关系1:时间变化速率(即时域信号的变化速率) 与 频谱 呈正比关系
对应关系2,时间周期T 与 频谱 :呈反比关系
对应关系3:脉冲宽度 与 频谱:呈反比关系
用脉冲宽度 定义带宽
频谱、幅度谱、相位谱、功率谱 与 周期性函数的频谱
周期函数、非周期函数的频谱总结,与对称频谱的意义
离散傅立叶变换与抽样:时域的抽样点数与频域点数的关系
傅立叶变换与正交性
傅立叶变换的 思想总结与优点
时域 的物理意义
频域 的物理意义
1,频域 的物理意义
2,傅立叶变换与谐波
3,傅立叶反变换与谐波叠加
4,带宽与时钟频率、脉冲宽度
关键技术点解释
1,IFFT反变换后各谐波如何叠加在一起?
2,什么是正交?正交的条件是什么?傅立叶变换后的谐波为什么一定是正交的?傅立叶反变换之前的频谱要满足什么条件?
3,为什么说时域上波形急剧变化,频域上就有很高的频率分量
4, 频域中幅值 与时域中的幅值 有什么关系?
5,采样
傅立叶变换的缺点
时域
频域
时域与频域的互相转换
傅立叶变换 原理
傅立叶变换 分类
傅立叶级数的五个公式(周期性函数)
傅立叶积分(非周期性函数)
振幅谱和相位谱的关系
功率谱
傅立叶变换推导出:时移原理与频移原理,对偶性质
时间-频率 间的对应关系。
对应关系1:时间变化速率(即时域信号的变化速率) 与 频谱 呈正比关系
对应关系2,时间周期T 与 频谱 :呈反比关系
对应关系3:脉冲宽度 与 频谱:呈反比关系
用脉冲宽度 定义带宽
频谱、幅度谱、相位谱、功率谱 与 周期性函数的频谱
周期函数、非周期函数的频谱总结,与对称频谱的意义
离散傅立叶变换与抽样:时域的抽样点数与频域点数的关系
傅立叶变换与正交性
傅立叶变换的 思想总结与优点
时域 的物理意义
频域 的物理意义
1,频域 的物理意义
2,傅立叶变换与谐波
3,傅立叶反变换与谐波叠加
4,带宽与时钟频率、脉冲宽度
关键技术点解释
1,IFFT反变换后各谐波如何叠加在一起?
2,什么是正交?正交的条件是什么?傅立叶变换后的谐波为什么一定是正交的?傅立叶反变换之前的频谱要满足什么条件?
3,为什么说时域上波形急剧变化,频域上就有很高的频率分量
4, 频域中幅值 与时域中的幅值 有什么关系?
5,采样
傅立叶变换的缺点
=================================
时域 的物理意义
虽然时域、频域都是信号的基本属性。但时域可视为日常可触摸到的领域,因为人类已经适应了时间、空间、大小这些概念。时域也是以时间为输入参数的函数,函数的输出值是信号的幅值,它与电压成正比。
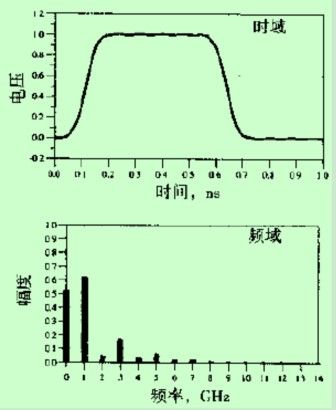
图 典型的时钟波形
时间单位有s:秒.us:微秒,ns:纳秒。中间的比值都是1000,即K.这样,1G=1000M,1M=1000K,因为T=1/f,所以1ns=1/1Ghz,可推断出上图中波形在时域的时钟频率 f=1G Hz。 注:这个f与频域中的频率不同,应该将f视为幅值随时间变化的速率,或时钟频率,在傅立叶变换中已经证明:基波频率=时域信号的时钟频率.
由上图可知,时钟波形的两个重要参数是时钟周期和上升时间。图中标明了1GHz时钟信号的时钟周期(1/1G)和10-90上升时间。下降时间一般要比上升时间短一些,有时会出现更多的噪声。
时钟周期就是时钟循环重复一次的时间间隔,通常用ns度量。时钟频率Fclock,即1秒钟内时钟循环的次数,是时钟周期Tclock的倒数。
上升时间与信号从低电平跳变到高电平所经历的时间有关,10-90上升时间,指信号从终值的10%跳变到90%所经历的时间
解释:上升时间越短(说明开关的电器件转得越快),频域的频谱越宽。
频域 的物理意义
时域以时间轴为坐标,频域分析是把信号变为以频率轴为坐标表示出来。横坐标是频率,纵坐标是幅值。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
频域,并不是日常生活中存在的实际概念,即非真实概念,而是一个数学概念。
频域,并不是日常生活中存在的实际概念,即非真实概念,而是一个数学概念。
傅立叶级数已经证明,
1,时域中任何波形都可以由无限多的正弦波叠加在一起而合成,所以时域中的波形可以经数学变换成无限多的的正弦波。 每个正弦波的时间速率不同,即频率不同。
2, 任何两个频率不同的正弦波都是正交的。如果将两个正弦波相乘并在整个时间轴上求积分,则积分值为零。这说明可以将不同的频率分量相互分离开。
1,时域中任何波形都可以由无限多的正弦波叠加在一起而合成,所以时域中的波形可以经数学变换成无限多的的正弦波。 每个正弦波的时间速率不同,即频率不同。
2, 任何两个频率不同的正弦波都是正交的。如果将两个正弦波相乘并在整个时间轴上求积分,则积分值为零。这说明可以将不同的频率分量相互分离开。
傅立叶变换与谐波
时域中分解出的每个正弦波对应频域中的一个频率。 运用频域的首要条件就是能够将波形从时域变换到频域,用傅立叶变换可以做到这一点。
对于
模拟信号,采用傅立叶积分。傅里叶积分是在整个时间轴上从 负无穷大 到 正无穷大 做积分,得到的结果是
零频率 到 正无穷大频率 上连续的频域函数。在这个区间上,每个连续的频率值都对应一个幅值。
图: 1GHz时钟信号在时域中的一个周期上的表示(上图)和在频域中的表示(下图)
时域的波形变换成频域中的一个个频率,下一张图也称为频谱图。
正弦波频率分量及其幅度的集合称为频谱,每一分量称为谐波;
在频域中,对波形的描述变为不同正弦波频率值的集合。每一个频率分量都有相关的幅度及相位,把所有这些频率值及其幅度值的集合称为波形的频谱。
理解关键点:
理解关键点:
1,
每个频率对应时域波形的一个正弦波分量。
2,
每个频率的幅值不同,其计算方式见下面的
An公式。频域中多个频率的幅值叠加后得到 时域中的最大幅值1(当时域上某个时间点时,所有正弦波分量会达到同相,此时所有正弦波分量波的叠加会达到时域中的最大幅值)。
3,
叠加的方法见“傅里叶反变换”部分。
4,FI奇偶谐波都有值。而DFT中只有奇次谐波有幅值。
上图中上一张图如果抽样量化为变为一个个离散的数据点,则使用离散傅里叶变换(DFT),将离散信号变换到频域中。快速傅里叶变换(FFT)适应于时域中的数据点个数是2的幂数的情况,如256点,512点或者1024点,它的优点是计算速率比DFT快100到10000倍。
上图中上一张图如果抽样量化为变为一个个离散的数据点,则使用离散傅里叶变换(DFT),将离散信号变换到频域中。快速傅里叶变换(FFT)适应于时域中的数据点个数是2的幂数的情况,如256点,512点或者1024点,它的优点是计算速率比DFT快100到10000倍。
对于DFT,频谱中仅存在某些频率值,这些值取决于时间间隔或重复频率的选择。频谱中的正弦波频率应是重复频率的整数倍。若时钟频率为1GHz,那么DFT就只有1GHz,2GHz,3GHz等正弦波分量。
第一个正弦波频率称为一次谐波,第二个正弦波频率称为二次谐波,依次类推。每个谐波都有不同的幅度和相位,所有谐波及其幅度的集合称为频谱。
采用DFT可以精确计算各个频率分量的幅度。所有偶次谐波(如2GHz,4GHz,6GHz)的幅度都为0,只存在奇次谐波的值。而0次谐波是直流分量,
奇次谐波的幅度 An,如式所示:
第一个正弦波频率称为一次谐波,第二个正弦波频率称为二次谐波,依次类推。每个谐波都有不同的幅度和相位,所有谐波及其幅度的集合称为频谱。
采用DFT可以精确计算各个频率分量的幅度。所有偶次谐波(如2GHz,4GHz,6GHz)的幅度都为0,只存在奇次谐波的值。而0次谐波是直流分量,
奇次谐波的幅度 An,如式所示:
An是n次谐波的幅度,
π是常量,为3.14159…
n是谐波数,为奇数
π是常量,为3.14159…
n是谐波数,为奇数
任何谐波的幅度都可由
2/(nπ)计算得出。 比如上图中:1次谐波幅值=2/(1*3.14)=0.63,
还有一个特殊的频率值:0Hz,即0次谐波,它是直流分量,其幅度与信号的均值相等。在方波占空比为50%的情况下,零次谐波幅度为0.5V。
傅立叶反变换与谐波叠加
从频谱变成时域波形的方法是:傅里叶反变换,它把每个频率分量变换成它的时域正弦波,再将其全部叠加。
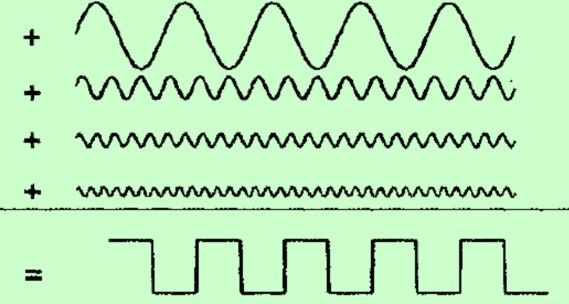
频域每个分量可转换成有多个时域的波(频率各不同),需要叠加以形成时域上传输的波形(上图中为 理想方波 )。
频域中的每个分量都是时域中定义在t=-∞到+∞的正弦波。为了重新生成时域波形,可以提取出频谱中描述的所有正弦波,并在时域中的每个时间间隔点处把它们叠加。从低频端开始,把频谱中的各次谐波叠加,就可得到时域中的波形。
对于1GHz理想方波的频谱,第一项是零次谐波,其幅度为0.5V。这个分量描述了时域中的直流常量。第二个分量是一次谐波,这在时域中是频率为1GHz、幅度为0.63V的正弦波。它与前一项叠加,在时域中得到均值偏移为0.5V的正弦波。这与理想方波的近似并不是很好,如图所示。
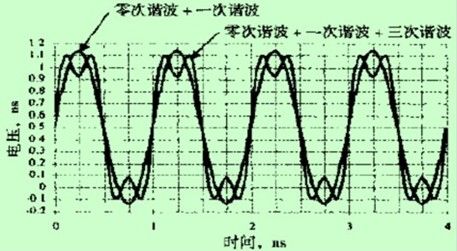
频域中的每个分量都是时域中定义在t=-∞到+∞的正弦波。为了重新生成时域波形,可以提取出频谱中描述的所有正弦波,并在时域中的每个时间间隔点处把它们叠加。从低频端开始,把频谱中的各次谐波叠加,就可得到时域中的波形。
对于1GHz理想方波的频谱,第一项是零次谐波,其幅度为0.5V。这个分量描述了时域中的直流常量。第二个分量是一次谐波,这在时域中是频率为1GHz、幅度为0.63V的正弦波。它与前一项叠加,在时域中得到均值偏移为0.5V的正弦波。这与理想方波的近似并不是很好,如图所示。

以“零次谐波+一次谐波”为例,0ns时,叠加后波形以0.5v开始。叠加后波形最高点当然是0.5v+0.63v=1.13v。(相位呢?\\)
将所有相继的高次谐波与已有波形想叠加,得出的结果会越来越像方波。
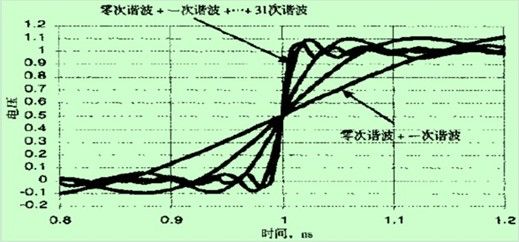
带宽用来表示频谱中有效的最高正弦波频率分量,为了充分近似时域波形的特征,这是需要包含的最高正弦波频率,所有高于带宽的频率分量都可忽略不计。
如果只用零次,一次和三次谐波合成时域波形,那么所得波形的带宽只达到三次谐波的值,即3GHz。设计时,这个波形的最高正弦波频率分量是3GHz,其他正弦波频率分量的幅度为零。
如果像上图那样增加更高次谐波来生成波形,那么设计的带宽为7GHz,19GHz和31GHz。这个波形中有效的最高正弦波频率分量就是31次谐波,即此波形的带宽为31GHz。
可以从叠加图中看到,最高正弦波频率分量越大,即带宽越大,则10-90上升时间就越短,与理想方波的波形就越接近。
思考:所以时域上波形急剧变化,频域上就会有很高的频率分量
已经证明:带宽与上升时间的倒数有关。BW=0.35/RT。RT表示10%-90%上升时间,单位为ns。BW表示带宽,单位为GHz。
已经证明:带宽与上升时间的倒数有关。BW=0.35/RT。RT表示10%-90%上升时间,单位为ns。BW表示带宽,单位为GHz。
带宽就是波形频谱中有效的最高正弦波频率分量。对信号而言,所谓的有效是基于信号的幅度与同频率理想方波的幅度相比较而言的。
带宽与时钟频率、脉冲宽度
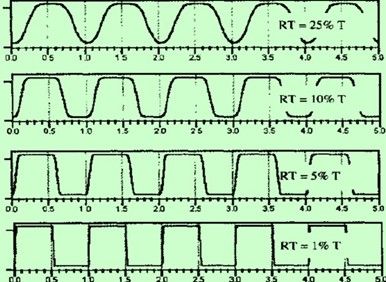
因为带宽与信号的上升时间有关。对两个不同的波形,可以有相同的时钟频率,但上升时间和带宽却很可能不同。仅知道时钟频率并不能告诉我们带宽,下图展示了四种不同的波形,每个波形的时钟频率都1GHz。然而它们的上升时间却不同,因此带宽也不同。
所以时域离散时,则频谱是连续函数。
关键技术点解释
1,IFFT反变换后各谐波如何叠加在一起?
不同频率正弦波分量,在时域的叠加是按照各正弦波波形在时间轴上进行几何叠加(即矢量和)。
由于各正弦波的频率、初相位、幅度都不同,所以叠加后的波形很可能不再是正弦信号,但一定是周期信号。 且周期、频率=基波正弦波的周期、频率。
两个正弦波偶尔同相时,会增加信号幅度,而异相减少了信号幅度。
由于各正弦波的频率、初相位、幅度都不同,所以叠加后的波形很可能不再是正弦信号,但一定是周期信号。 且周期、频率=基波正弦波的周期、频率。
两个正弦波偶尔同相时,会增加信号幅度,而异相减少了信号幅度。
由于正弦波用sinx与cosx表示(正弦波sinx可以转化为余弦波
cosx),所以 正弦波 叠加符合 三角函数 的加法运算法则,即
比如某个正弦波分量的表示方法与时域图形如下:
多个正弦波函数加在一起,使用以下的运算法则
可以看出:两个三角函数加在一起后,相位会变化。
举例如下:
这时:原正弦波是有初相,但 叠加 后波形的初相发生变化。
有一个flash动画,非常好的表现了( 不同频率正弦波分量叠加的波形)叠加过程。见 http://physics.seu.edu.cn/phycourse/phycourse/Photo/UploadPhotos/200710/20071030113553718.swf
举例:
同振幅不同频率的正弦波叠加,频谱特点与波形特点
1.频谱特点:
当有n个同幅值、不同频率的信号叠加时,其合成信号的频谱图就是由这n条长度相同、且位于这n个频率点的谱线组成。可以看到:频谱是不连续的。
2.波形叠加特点:
叠加后波形的形状与各信号的频率、初相、幅值有关,虽然不再是正弦信号,但一定是周期信号,且周期与最低频率分量的信号周期相同。
相差π/2的两个正弦波叠加出来的波形是怎么样的
答:
首先要看这两个正弦波的初相位是怎样的,你的问题太不具体了,并没有给出这两个正弦波的初相位。
总的来讲,两个初相位不同正弦波其叠加后的波形可能是各种各样的,比如说,如果两个正弦波的初相位正好相差π,那么它们的叠加正好是一条直线,而如果它们的初相位相差2π,那么它们叠加后波形不变,只是振幅变为原来的2倍。
总之,两列正弦波叠加后,振动方向相同的总振幅为两列波振幅之和,方向不变;振动方向不相同的总振幅为两列波振幅之差,方向与绝对值大者相同。
参看初中物理课本,有关振动的章节
1.频谱特点:
当有n个同幅值、不同频率的信号叠加时,其合成信号的频谱图就是由这n条长度相同、且位于这n个频率点的谱线组成。可以看到:频谱是不连续的。
2.波形叠加特点:
叠加后波形的形状与各信号的频率、初相、幅值有关,虽然不再是正弦信号,但一定是周期信号,且周期与最低频率分量的信号周期相同。
相差π/2的两个正弦波叠加出来的波形是怎么样的
答:
首先要看这两个正弦波的初相位是怎样的,你的问题太不具体了,并没有给出这两个正弦波的初相位。
总的来讲,两个初相位不同正弦波其叠加后的波形可能是各种各样的,比如说,如果两个正弦波的初相位正好相差π,那么它们的叠加正好是一条直线,而如果它们的初相位相差2π,那么它们叠加后波形不变,只是振幅变为原来的2倍。
总之,两列正弦波叠加后,振动方向相同的总振幅为两列波振幅之和,方向不变;振动方向不相同的总振幅为两列波振幅之差,方向与绝对值大者相同。
参看初中物理课本,有关振动的章节
2,什么是正交?正交的条件是什么?傅立叶变换后的谐波为什么一定是正交的?傅立叶反变换之前的频谱要满足什么条件?
正交最早出现于三维空间中的向量分析。 在3维向量空间中, 两个向量的内积 如果是零, 那么就说这两个向量是正交的。 换句话说, 两个向量正交意味着它们是相互垂直的。向量α与β正交,记为α⊥β。
对于傅立叶变换有关的信号分析来说,首先要知道一个基本原则:在三角函数系中任何不同的两个函数的乘积在区间[-π,π]上的积分等于0。 三角函数系即:{1,cosx,sinx,cos2x,sin2x,……,cosnx,sinnx,……}
在区间[-π,π]上正交,就是指在三角函数系⑴中任何不同的两个函数的乘积在区间[-π,π]上的积分等于0,即
∫[-π->π]cosnxdx=0
∫[-π->π]sinnxdx=0
∫[-π->π]sinkxcosnxdx=0
∫[-π->π]coskxcosnxdx=0
∫[-π->π]sinkxsinnxdx=0 (k,n=1,2,3.....,k≠n)
对于傅立叶变换有关的信号分析来说,首先要知道一个基本原则:在三角函数系中任何不同的两个函数的乘积在区间[-π,π]上的积分等于0。 三角函数系即:{1,cosx,sinx,cos2x,sin2x,……,cosnx,sinnx,……}
在区间[-π,π]上正交,就是指在三角函数系⑴中任何不同的两个函数的乘积在区间[-π,π]上的积分等于0,即
∫[-π->π]cosnxdx=0
∫[-π->π]sinnxdx=0
∫[-π->π]sinkxcosnxdx=0
∫[-π->π]coskxcosnxdx=0
∫[-π->π]sinkxsinnxdx=0 (k,n=1,2,3.....,k≠n)
在傅立叶级数公式
(傅立叶公式2)中可知:
时域f(t)信号的第k个谐波是S(k)=AkCosWkt+BkSinWkt,它即f(t)的第k个频率分量对应的正弦波表示。
那么S(k)与S(m)即为第K个谐波与第m个谐波。
根据积分运算法则:两个函数的积分=这两个函数积分的和,常数与函数f(x)乘积的积分=常数与函数f(x)的积分的乘积。
再加上提到的三角函数系的积分关系。可以容易计算出:
当k与m不相等时,可以得出S(k)与S(m)的乘积在区间[-T,T]上的积分=0,T为时域原信号的周期。
即:频域任意两个信号之间是正交的。这两个信号以频率为参数,可视为两个子信道的信号。
而时域信号f(t),转换为傅立叶级数表示法后,与任一个谐波( 如S(k) )相乘后在区间[-T,T]取积分,其结果设为G。也可以很容易计算出:G中只包括了 S(K)与常数的乘积,而滤掉了其它谐波(S(m),m!=K)。类似于傅立叶级数中求an的计算方法,见下
那么S(k)与S(m)即为第K个谐波与第m个谐波。
根据积分运算法则:两个函数的积分=这两个函数积分的和,常数与函数f(x)乘积的积分=常数与函数f(x)的积分的乘积。
再加上提到的三角函数系的积分关系。可以容易计算出:
当k与m不相等时,可以得出S(k)与S(m)的乘积在区间[-T,T]上的积分=0,T为时域原信号的周期。
即:频域任意两个信号之间是正交的。这两个信号以频率为参数,可视为两个子信道的信号。
而时域信号f(t),转换为傅立叶级数表示法后,与任一个谐波( 如S(k) )相乘后在区间[-T,T]取积分,其结果设为G。也可以很容易计算出:G中只包括了 S(K)与常数的乘积,而滤掉了其它谐波(S(m),m!=K)。类似于傅立叶级数中求an的计算方法,见下
即:OFDM接收机可以解调的原理。
所以 在OFDM接收机解调时,在整个符号周期内分别用对于 OFDM符号*每个子载波频域点对应谐波信号 后再积分,可以分解出每个子信道符号出来 ,因为每个子载波频域谐波信号表达式 是接收机可以自行产生的 )
这就是OFDM发射机侧
IFFT运算前各子载波应该满足的关系。
3,为什么说时域上波形急剧变化,频域上就有很高的频率分量
时域上波形急剧变化,使波产生了吉布斯现象。所谓吉布斯现象就是用有限次谐波分量来近似原信号,在不连续点将出现过冲,过冲峰值不随谐波分量增加而减少,且为跳变值的9%
f(t)=cos(t) 与f(t)=cos(t)+cos(100000t)在时域波形上哪个变化快呢?在频域就会反映出来了
f(t)=cos(t) 与f(t)=cos(t)+cos(100000t)在时域波形上哪个变化快呢?在频域就会反映出来了
这也符合:上升时间越短,带宽越大。
4. 频域中幅值 与时域中的幅值 有什么关系?
幅值绝对不一样,除非是正弦信号这类频谱分量只有一条竖线的信号。一般的信号的频谱分量非常丰富,这些所有的频率分量的幅值叠加起来才是时域里面信号的真实幅值。比如假设有个时域信号的幅值为9,分解到频谱出现4个不同频率的分量F1,F2,F3,F4,这四个分量的幅值之和才是9,单个是不能比的。
至于频率,如上所示那肯定是不一样的啦。其实把周期信号时域变换到频域也就是先把一个f为频率的信号分解成很多个各种各样频率的小信号,里面有f1,f2,f3,f4,......这些频率有的大于f,有的小于f,然后再画一条f作x轴,幅值作y轴的直角坐标系,把每个小频率对应的幅值画进去。
4. 频域中幅值 与时域中的幅值 有什么关系?
幅值绝对不一样,除非是正弦信号这类频谱分量只有一条竖线的信号。一般的信号的频谱分量非常丰富,这些所有的频率分量的幅值叠加起来才是时域里面信号的真实幅值。比如假设有个时域信号的幅值为9,分解到频谱出现4个不同频率的分量F1,F2,F3,F4,这四个分量的幅值之和才是9,单个是不能比的。
至于频率,如上所示那肯定是不一样的啦。其实把周期信号时域变换到频域也就是先把一个f为频率的信号分解成很多个各种各样频率的小信号,里面有f1,f2,f3,f4,......这些频率有的大于f,有的小于f,然后再画一条f作x轴,幅值作y轴的直角坐标系,把每个小频率对应的幅值画进去。
5,采样
来自维基百科,
采样定理,又称香农采样定理,奈奎斯特采样定理,是
信息论
,特别是
通讯
与
信号处理
学科中的一个重要基本结论.
E. T. Whittaker
(1915年发表的统计理论),
克劳德·香农
与
Harry Nyquist
都对它作出了重要贡献。另外,
V. A. Kotelnikov
也对这个定理做了重要贡献。
采样
是将一个信号(即时间或空间上的连续函数)转换成一个数值序列(即时间或空间上的离散函数)。采样定理指: 如果信号是
带限
的,并且
采样频率
高于信号
带宽
的一倍,那么,原来的连续信号可以从采样样本中完全重建出来。
带限信号变换的快慢受到它的最高频率分量的限制,也就是说它的离散时刻采样表现信号细节的能力是有限的。采样定理是指,如果信号带宽小于
奈奎斯特频率
(即采样频率的二分之一),那么此时这些离散的采样点能够完全表示原信号。高于或处于奈奎斯特频率的频率分量会导致
混叠
现象。大多数应用都要求避免混叠,混叠问题的严重程度与这些混叠频率分量的相对强度有关。
连续信号在时间(或空间)上以某种方式变化着,而
采样
过程则是在时间(或空间)上,以T为单位间隔来测量连续信号的值。T称为
采样间隔
。在实际中,如果信号是时间的函数,通常他们的
采样间隔
都很小,一般在毫秒、微秒的量级。采样过程产生一系列的数字,称为
样本
。
样本
代表了原来地信号。每一个样本都对应着测量这一样本的特定时间点,而
采样间隔
的倒数,1/T即为
采样频率
,fs,其单位为样本/秒,即
赫兹
(hertz)。
信号的重建是对样本进行插值的过程,即,从离散的样本x[n]中,用数学的方法确定连续信号x(t)。
信号的重建是对样本进行插值的过程,即,从离散的样本x[n]中,用数学的方法确定连续信号x(t)。
六,傅立叶变换的缺点
傅里叶变换具有良好的性质,能够实现时域到频域相互转换,它实质是将f(t)这个波形分解成许多 不同频率的正弦波的叠加。这样我们就可以把对原函数f(t)的研究转化为 不同频率分量的幅值和 相位的研究。 从傅里叶变换公式可以看出,它是以 正弦波及其高次谐波为标准基的 ,因此它 是对信 号的一种总体上的分析,具有单一的局部定位能力, 也就是在 时域的良好定位是以频域的全部信号 分析为代价的,对频域的良好定位是以时域的全部信号分析为代价的, 时域和频域分析具有分析上 的矛盾,傅立叶变换的频率谱中要么频率是准确的而时间是模糊的,要么时间是准确的而频率是 模糊的,它不可能同时在时域和频域都具有良好的定位的能力。 傅立叶变换是建立在平稳信号的 基础上的,在非平稳时变信号的分析上,它却无能为力。
傅立叶变换把信号的时域特征和频域特征联系在一起,使我们可以从信号的时域和频域两个 角度观察和分析信号,但是 二者却是绝对分离的,即在频域不包含任何时域信息,在时域中同样 找不到任何频域信息的影子。对于傅立叶频谱中的某一频率,不知道这一频率是何时产生的, 只能从全局上分析信号。这样在信号分析中就面临一对最基本的矛盾:时域和频域的局部化矛盾