NOIP2003提高组

 

第一题 神经网络

【题目描述】

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

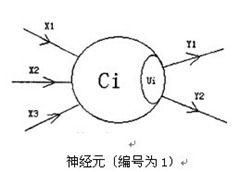
图中，X1—X3是信息输入渠道，Y1－Y2是信息输出渠道，C1表示神经元目前的状态，Ui是阈值，可视为神经元的一个内在参数。
神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

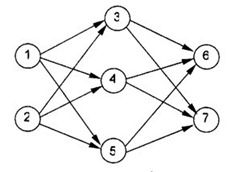
兰兰规定，Ci服从公式：（其中n是网络中所有神经元的数目）

 

 

公式中的Wji（可能为负值）表示连接j号神经元和 i号神经元的边的权值。当 Ci大于0时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为Ci。如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。
现在，给定一个神经网络，及当前输入层神经元的状态（Ci），要求你的程序运算出最后网络输出层的状态。

 

【输入格式】

输入文件第一行是两个整数n（1≤n≤200）和p。接下来n行，每行两个整数，第i＋1行是神经元i最初状态和其阈值（Ui），非输入层的神经元开始时状态必然为0。再下面P行，每行由两个整数i，j及一个整数Wij，表示连接神经元i、j的边权值为Wij。

 

【输出格式】

输出文件包含若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状
态，两个整数间以空格分隔。仅输出最后状态非零的输出层神经元状态，并且按照编号由
小到大顺序输出！
若输出层的神经元最后状态均为 0，则输出 NULL。

 

【样例输入】

5 6
1 0
1 0
0 1
0 1
0 1
1 3 1
1 4 1
1 5 1
2 3 1
2 4 1
2 5 1 

 
【样例输出】

3 1

4 1

5 1

 

【分析】

用递归写的话，很好写恩。注意题目中给的判定条件。

 

第二题 侦探推理

忽略囧。

 

第三题 加分二叉树

【题目描述】

设一个n个节点的二叉树tree的中序遍历为（l,2,3,…,n），其中数字1,2,3,…,n为节点编号。每个节点都有一个分数（均为正整数），记第i个节点的分数为di，tree及它的每个子树都有一个加分，任一棵子树subtree（也包含tree本身）的加分计算方法如下：
subtree的左子树的加分× subtree的右子树的加分＋subtree的根的分数
若某个子树为空，规定其加分为1，叶子的加分就是叶节点本身的分数。不考虑它的空子树。
试求一棵符合中序遍历为（1,2,3,…,n）且加分最高的二叉树tree。要求输出；
（1）tree的最高加分
（2）tree的前序遍历

 

【输入格式】

第1行：一个整数n（n＜30），为节点个数。
第2行：n个用空格隔开的整数，为每个节点的分数（分数＜100）。

 

【输出格式】

第1行：一个整数，为最高加分（结果不会超过4,000,000,000）。
第2行：n个用空格隔开的整数，为该树的前序遍历。

 

【样例输入】

5
5 7 1 2 10 

 
【样例输出】

145
3 1 2 4 5 

 
【分析】

区间动归。

 

第四题 传染病控制

【题目描述】

近来，一种新的传染病肆虐全球。蓬莱国也发现了零星感染者，为防止该病在蓬莱国大范围流行，该国政府决定不惜一切代价控制传染病的蔓延。不幸的是，由于人们尚未完全认识这种传染病，难以准确判别病毒携带者，更没有研制出疫苗以保护易感人群。于是，蓬莱国的疾病控制中心决定采取切断传播途径的方法控制疾病传播。经过 WHO（世界卫生组织）以及全球各国科研部门的努力，这种新兴传染病的传播途径和控制方法已经研究消楚，剩下的任务就是由你协助蓬莱国疾控中心制定一个有效的控制办法。

研究表明，这种传染病的传播具有两种很特殊的性质；

第一是它的传播途径是树型的，一个人X只可能被某个特定的人Y感染，只要Y不
得病，或者是XY之间的传播途径被切断，则X就不会得病。

第二是，这种疾病的传播有周期性，在一个疾病传播周期之内，传染病将只会感染一
代患者，而不会再传播给下一代。

这些性质大大减轻了蓬莱国疾病防控的压力，并且他们已经得到了国内部分易感人群的潜在传播途径图（一棵树）。但是，麻烦还没有结束。由于蓬莱国疾控中心人手不够，同时也缺乏强大的技术，以致他们在一个疾病传播周期内，只能设法切断一条传播途径，而没有被控制的传播途径就会引起更多的易感人群被感染（也就是与当前已经被感染的人有传播途径相连，且连接途径没有被切断的人群）。当不可能有健康人被感染时，疾病就中止传播。所以，蓬莱国疾控中心要制定出一个切断传播途径的顺序，以使尽量少的人被感染。你的程序要针对给定的树，找出合适的切断顺序。

 

【输入格式】

输入格式的第一行是两个整数n（1≤n≤300）和p。表示有N个人，接下来p行，每一行有两个整数i和j，表示节点i和j间有边相连（意即，第i人和第j人之间有传播途径相连）。其中节点1是已经被感染的患者。

 

【输出格式】

只有一行，输出总共被感染的人数。

 

【样例输入】

7 6
1 2
1 3
2 4
2 5
3 6
3 7 

 
【样例输出】

3

 

【分析】

很自然的会想到贪心，但是应该用搜索。贪心是不对的。

对于第K个周期。首先我们计算下一个周期有哪些点是被传染了的。然后枚举下一个周期中的点哪一个被切断。因为tot是全局变量，所以记得要减会tot的值。

代码

第一题

#include <stdio.h>

#define MAXN 210

int pre[MAXN][MAXN],c[MAXN],u[MAXN],w[MAXN][MAXN];

bool end[MAXN],v[MAXN];

bool have;

int n,m,x,y,z;

void find(int x) {

  if (v[x])

    return;

  v[x] = 1;

  int tem = 0;

  for (int i = 1;i <= pre[x][0];++i) {

    int y = pre[x][i];

    find(y);

    if (c[y] > 0)

      tem += w[y][x] * c[y];

  }

  tem -= u[x];

  c[x] = tem;

}

int main() {

  scanf("%d%d",&n,&m);

  for (int i = 1;i <= n;++i) {

    scanf("%d%d",&c[i],&u[i]);

    if (c[i] != 0)

      v[i] = 1;

  }

  for (int i = 1;i <= m;++i) {

    scanf("%d%d%d",&x,&y,&z);

    w[x][y] = z;

    pre[y][++pre[y][0]] = x;

    end[x] = 1;

  }

  for (int i = 1;i <= n;++i)

    if (!end[i]) {

      find(i);

      if (c[i] > 0) {

        have = 1;

        printf("%d %d\n",i,c[i]);

      }

    }

  if (!have)

    printf("NULL\n");

  return 0;

}

 

第三题

#include <stdio.h>

#define MAXN 60

int f[MAXN][MAXN],mid[MAXN][MAXN],a[MAXN];

int n;

int find(int x,int y) {

  if (x > y)

    return 1;

  if (f[x][y])

    return f[x][y];

  if (x == y)

    f[x][y] = a[x];

  else {

    int tem;

    for (int i = x;i <= y;++i) {

      tem = find(x,i - 1) * find(i + 1,y) + a[i];

      if (tem > f[x][y]) {

        f[x][y] = tem;

        mid[x][y] = i;

      }

    }

  }

  return f[x][y];

}

void out(int x,int y) {

  if (x > y)

    return;

  if (x == y)

    printf("%d ",x);

  else {

    printf("%d ",mid[x][y]);

    out(x,mid[x][y] - 1);

    out(mid[x][y] + 1,y);

  }

}

int main() {

  scanf("%d",&n);

  for (int i = 1;i <= n;++i)

    scanf("%d",&a[i]);

  printf("%d\n",find(1,n));

  out(1,n);

  return 0;

}

第四题

#include <stdio.h>

#include <limits.h>

#define MAXN 310

int f[MAXN],bl[MAXN][MAXN];

int ans = INT_MAX,n,p,x,y,tot;

void build(int x) {

  for (int i = 1;i <= bl[x][0];++i) {

    int y = bl[x][i];

    int j;

    for (j = 1;j <= bl[y][0];++j)

      if (bl[y][j] == x)

        break;

    bl[y][j] = bl[y][bl[y][0]--];

    build(y);

  }

}

void find(int k) {

  if (tot > ans)

    return;

  int t = 0;

  for (int i = 1;i <= n;++i)

    if (f[i] == k)

      for (int j = 1;j <= bl[i][0];++j) {

        f[bl[i][j]] = k + 1;

        ++tot;

        t = 1;

      }

  --tot;

  for (int i = 1;i <= n;++i)

    if (f[i] == k + 1) {

      f[i] = 0;

      find(k + 1);

      f[i] = k + 1;

    }

  ++tot;

  for (int i = 1;i <= n;++i)

    if (f[i] == k + 1) {

      f[i] = 0;

      --tot;

    }

  if ((!t) && (tot < ans))

    ans = tot;

}

int main() {

  scanf("%d%d",&n,&p);

  for (int i = 1;i <= p;++i) {

    scanf("%d%d",&x,&y);

    bl[x][++bl[x][0]] = y;

    bl[y][++bl[y][0]] = x;

  }

  build(1);

  f[1] = 1;

  tot = 1;

  find(1);

  printf("%d\n",ans);

  return 0;

}