zju 1134 树形dp

本题的数学模型在题目中已明示，我们将其用数学语言重述一遍：在图G=(V,E)中找一顶点集S，使得对任意(u,v)∈E有u∈S或v∈S，且|S|最小。很明显，这是求图的最小顶点覆盖集。

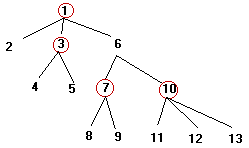
　图的最小顶点覆盖是NP问题，至今还没有有效算法。而本题N的规模可达1500，显然用搜索是无法完成的。但本题的图十分特殊是一棵树。为了进一步利用数据结构的特殊性，我们不妨先手工分析一个例子。左图为一个有13个顶点的树，其中用红色圈出的顶点为找到的最小覆盖集。很明显，叶节点不可能属于覆盖集，但叶节点的父节点一定属于覆盖集，以此为基础再判断上一层次节点是否属于覆盖集。左图的节点编号从大到小正好是我们判断的顺序，该顺序恰好是树的前序遍历顺序，由此我们可得出本题的算法：

　　 1：procedure Min-Vertex-Cover(T);
　　2：begin
　　3： 　按前序遍历顺序重新编排整棵树的节点编号。
　　4： 　for I:=1 to n do cover[I]:=0;
　　5： 　for I:=n Downto 2 do
　　6： 　　if (cover[I]=0) and (cover[parent[I]]=0) then
　　7： 　　　　cover[parent[I]]:=1;
　　8：end;
　　
　　该算法是一个贪心算法。算法中用数组cover来标记选入覆盖点集的树结点，即当结点i被选入覆盖点集，则cover[i]=1，否则cover[i]=0。为了说明算法的正确性，必须证明关于树的最小顶点覆盖问题满足贪心选择性质并且具有最优子结构性质。具体的证明过程，在《若干NP完全问题的特殊情形》一文中已有详细的叙述。

另外，本题的图是一棵树，很容易想到动态规划（树形dp)
设dp[i][0]表示节点i不设置在最小覆盖集的情况下以i为根的子树的最小覆盖集中元素的个数
dp[i][1]表示节点i再最小覆盖集中的情况下以i为根的子树的最小覆盖集中元素的个数
则状态转移方程为:
当i不是叶子节点时：
dp[i][0]=dp[j1][1]+dp[j2][1]+...+dp[jm][1] （j1,j2,j3,..,jm都是i的子节点)
dp[i][1]=min(dp[j1][0],dp[j1][1])+min(dp[j2][0],dp[j2][1])+...+min(dp[jm][0],dp[jm][1])+1 （j1,j2,j3,..,jm都是i的子节点)
当i是叶子节点时:
dp[i][0]=0
dp[i][1]=1
那么最后的结果就是 min(dp[root][0],dp[root][1])

第一种算法（贪心）代码:

// 贪心算法
#include  < stdio.h >
#include  < string .h >
#define  MAXN 1500

int  parent[MAXN + 1 ],covert[MAXN + 1 ],cover[MAXN + 1 ];
int  count,n;

void  preorder( int  root)  {
    covert[count++]=root;
    for(int i=0;i<n;i++)
        if(parent[i]==root)
            preorder(i);
}

int  main()  {
    int j,m,t,root;
    while(scanf("%d",&n)!=EOF) {
        for(int i=0;i<n;i++) parent[i]=-1;
        for(int i=0;i<n;i++) {
            scanf("%d:(%d)",&j,&m);
            for(int k=0;k<m;k++) {
                scanf("%d",&t);
                parent[t]=j;
            }
        }
        memset(cover,0,sizeof cover);
        count=1;
        root=-1;
        do{
            root++;
        }while(parent[root]!=-1);
        preorder(root);
        count=0;
        for(int i=n;i>=2;i--) 
            if(cover[covert[i]]==0&&cover[parent[covert[i]]]==0) {
                cover[parent[covert[i]]]=1;
                count++;
            }
        printf("%d\n",count);
    }
    return 0;
}

第二种算法(dp)代码:

// 树形dp
#include  < stdio.h >
#include  < string .h >
#define  MAXN 1500

int  parent[MAXN + 1 ];
int  dp[MAXN + 1 ][ 3 ];
int  n;

inline  int  min( int  a, int  b)  { return a<b?a:b; }
void  dfs( int  root)  {
    bool leaf=true;
    int s1=0,s2=0;
    for(int i=0;i<n;i++) {
        if(parent[i]==root) {
            leaf=false;
            dfs(i);
            s1+=dp[i][1];
            s2+=min(dp[i][0],dp[i][1]);
        }
    }
    if(leaf) {
        dp[root][0]=0;
        dp[root][1]=1;
    }else{
        dp[root][0]=s1;
        dp[root][1]=s2+1;
    }
}
    
int  main()  {
    int i,j,k,m,t,root;
    while(scanf("%d",&n)!=EOF) {
        memset(parent,255,sizeof parent);
        for(i=0;i<n;i++) {
            scanf("%d:(%d)",&j,&m);
            for(k=0;k<m;k++) {
                scanf("%d",&t);
                parent[t]=j;
            }
        }
        root=-1;
        do{ root++; } while(parent[root]!=-1);
        dfs(root);
        printf("%d\n",min(dp[root][0],dp[root][1]));
    }
    return 0;
}