2014 Super Training #7 E Calculate the Function --矩阵+线段树

原题：ZOJ 3772 http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3772

这题算是长见识了，还从没坐过矩阵+线段树的题目呢，不要以为矩阵就一定配合快速幂来解递推式的哦。

由F(x)=F(x-1)+F(x-2)*A[x]，转化为矩阵乘法：

 ===》

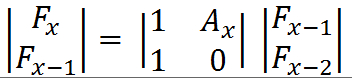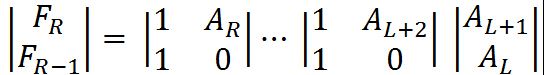
所以维护一颗线段树，线段树的每个结点保存一个矩阵，叶子节点为： a[0][0] = a[1][0] = 1, a[0][1] = Ax, a[1][1] = 0的形式

否则保存 a[r] * a[r-1] * ... * a[l] 的结果矩阵，且要注意不要乘反了。

代码：

#include <iostream>

#include <cstdio>

#include <cstring>

#include <cmath>

#include <cstdlib>

#include <algorithm>

#define Mod 1000000007

#define ll long long

using namespace std;

#define N 100007



struct Matrix

{

    ll m[2][2];

    Matrix(int _x)

    {

        m[0][0] = 1;

        m[0][1] = _x;

        m[1][0] = 1;

        m[1][1] = 0;

    }

    Matrix(){}

}tree[4*N];

ll A[N];



Matrix Mul(Matrix a,Matrix b)

{

    Matrix c;

    memset(c.m,0,sizeof(c.m));

    for(int i=0;i<2;i++)

        for(int j=0;j<2;j++)

            for(int k=0;k<2;k++)

                c.m[i][j] = (c.m[i][j] + a.m[i][k]*b.m[k][j])%Mod;

    return c;

}



void build(int l,int r,int rt)

{

    if(l == r)

    {

        tree[rt] = Matrix(A[l]);

        return;

    }

    int mid = (l+r)/2;

    build(l,mid,2*rt);

    build(mid+1,r,2*rt+1);

    tree[rt] = Mul(tree[2*rt+1],tree[2*rt]);  //注意不要乘反了

}



Matrix query(int l,int r,int aa,int bb,int rt)

{

    if(aa<=l && bb>=r)

        return tree[rt];

    int mid = (l+r)/2;

    if(aa>mid)

        return query(mid+1,r,aa,bb,2*rt+1);

    else if(bb<=mid)

        return query(l,mid,aa,bb,2*rt);

    else

        return Mul(query(mid+1,r,aa,bb,2*rt+1),query(l,mid,aa,bb,2*rt)); //不要乘反

}



int main()

{

    int n,m;

    int i,t;

    int aa,bb;

    scanf("%d",&t);

    while(t--)

    {

        scanf("%d%d",&n,&m);

        for(i=1;i<=n;i++)

            scanf("%lld",&A[i]);

        build(1,n,1);

        while(m--)

        {

            scanf("%d%d",&aa,&bb);

            if(bb-aa<=1)

                printf("%lld\n",A[bb]);

            else

            {

                Matrix ans = query(1,n,aa+2,bb,1);

                ll res = ans.m[0][0]*A[aa+1]%Mod + ans.m[0][1]*A[aa]%Mod;

                printf("%lld\n",res%Mod);

            }

        }

    }

    return 0;

}

View Code