Coursera台大机器学习课程笔记6 -- The VC Dimension
本章的思路在于揭示VC Dimension的意义,简单来说就是假设的自由度,或者假设包含的feature vector的个数(一般情况下),同时进一步说明了Dvc和,Eout,Ein以及Model Complexity Penalty的关系。
一回顾

由函数B(N,k)的定义,可以得到比较松的不等式mh(N)小于等于N^(k-1)(取第一项)。

这样就可以把不等式转化为仅仅只和VC Dimension和N相关了,从而得出如下结论:
1 mh(N)有break point k,那么其就是多项式级别的,我们认为假设数量不算多,是个好的假设;
2 N 足够大,这样我们便算有了好的抽样数据集(假设不含很多Noise);
=〉这两点由上述不等式可以推导这样的机器学习算法有好的泛化能力,其在全集上会有和在D上一致的表现;
3 如果算法选择的是小的Ein
=>最终我们可以推断机器可以学习,因为其在全集数据集错误率会较低。
二什么是VC Dimension
下面给出了VC Dimension的定义,
- 它是该假设集能够shatter的最多inputs的个数,即最大完全正确的分类能力(注意,只要存在一种分布的input能够正确分类就算是,这才叫最大);
- 它是最小的k-1,这个很好理解,最小的k是假设集不能shatter任何分布类型的inputs的最少个数,和VC Dimension正好相反;

同样,将Dvc替换k,得到mh(N)<=N^(Dvc)
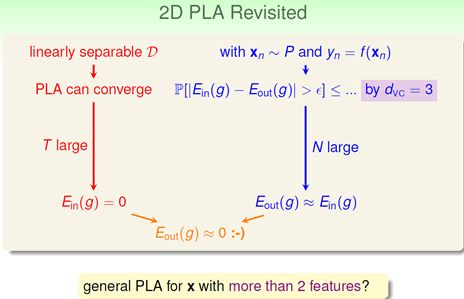
三 VC Dimension 和 Feature 数量的关系,在PLA算法中
接下来回顾了PLA在2d情况下,由于其Dvc=3,所以按照算法我们选小的Ein就能够保证机器学习算法的运行,但是这是2维的情况,对于多维呢?也就是说增加feature咋办?
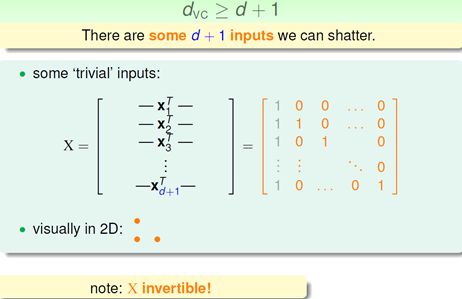
这里又抛出了一个结论:Dvc = d+1, d为feature vector的维度。
要证明这个等式,可以将它分为两块证明,
1 证明 Dvc >= d+1;
2 证明 Dvc <= d+1;
首先证明等式1:
因为Dvc >= d+1, 那么我们必然可以shatter 某一类的d+1的inputs,这个是VC Dimension的定义。这里用线性代数的方法表达了X矩阵的每一行是一个x向量的转置。这个有意构造的X便能够被shatter。首先,shatter的本质是H对X的每个判断都是对的即等于y,所以有如下不等式:
X*W = Y,我们注意到X是可逆的,所以W = X^(-1) * Y,所以我们只要让feature vector等于X的逆矩阵乘以Y就能给完全shatter X,言外之意,只要我们构造的inputs其有逆矩阵就能够被shatter!
下面证明等式二,Dvc<=d+1,也就是说对于d+2的inputs,其一定不能被shatter,同样我们构造一个X,这次是任意的,其包含d+2个inputs,我们发现这个矩阵的列为d+1而行为d+2,由线性代数的知识,我们知道这d+2个向量的某一个可以表示为另外d+1个向量的线性组合,假设这个向量为Xd+2,那么便有了如下等式:
w^Txd+2 = a1w^Tx1 + a2w^Tx2 + ... + ad+1w^Txd+1,
我们只要构造这样这组w,保证每一项是正的,例如假设a1是负的,那么我们构造w使得w^Tx1也是负的,这样就使得最终的值为正,从而我们没法分类其为负的情况,因为其值始终是正的。换句话说,因为d+2是前d+1的线性组合,这样一个限制导致了最终的结果。所以对于d+2我们无法完全分类,也即使Dvc<=d+1。

四 VC Dimension的直观理解
那么VC Dimension本质上到底是什么呢?
下图给了答案

自由度的概念,体现在我们能够包含多少feature w,能够有多少假设H的数量,以及我们最终的分类能力Dvc,也就是说Dvc本质上大体上是H的分类能力,同样可以理解为feature的个数,假设的个数,因为它们都是互相成正比的。
再次回到以前那个泛化不等式:

将它左右变形,求出Eout的的界限,我们比较关注上限,可知我们最终的机器学习算法其在整体的错误率和N,H,S的表达式(Model 复杂度的惩罚)有关。下图很直观的给出了它们之间的关系:

这个图说了:
1 Dvc越高 -> Ein下降(shatter能力变强)-> model complexity的penalty提高,导致Eout先降后升
2 Dvc越低 -> Ein升高 -> model complexity的penalty降低,Eout最终也是会上升
所以最好情况的Eout是我们选取Dvc在中间的情况,这样Ein和penalty都不高,即最终的Eout也不会太高。这也就是为什么,我们不能够盲目增加feature也不能有太少feature的原因。
五总结
本章主要描述了VC Dimension并给出了较为直观的解释,我们不能盲目增加VC Dimension也不能太低,而应该去中间值,这样既保证Ein不高也保证model complexity的penalty不高。