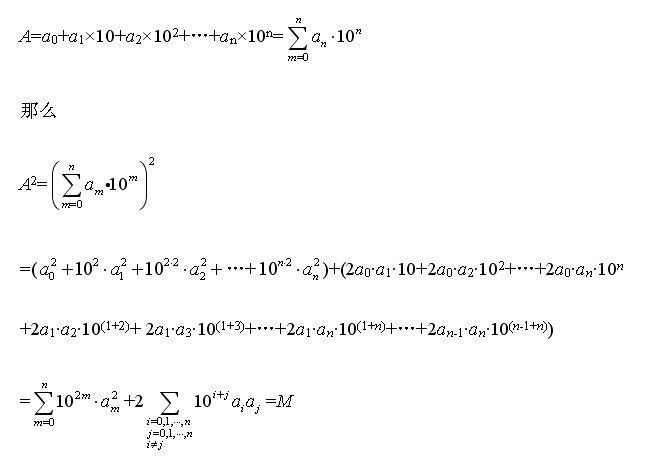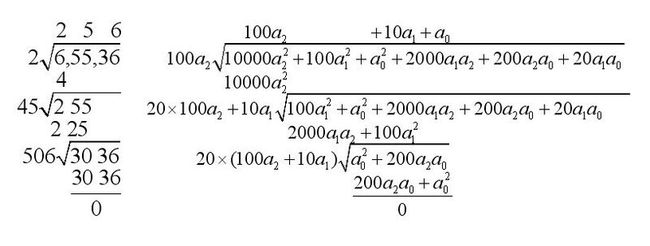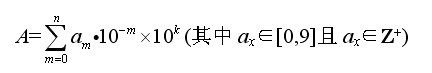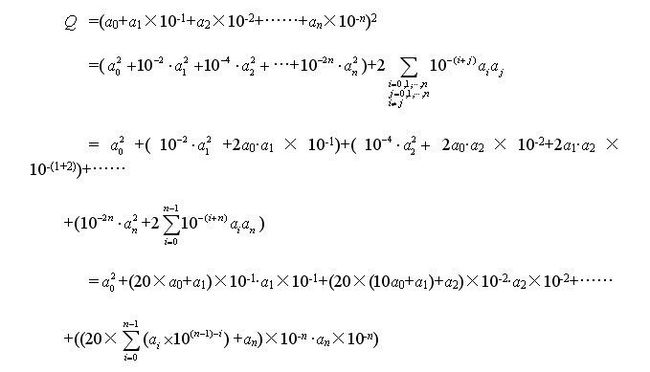数学/手开平方/sgu111 Very simple problem
题意
给出一个数n,求sqrt(n) (1≤n≤101000)
分析
题意很简单,就是开一个数的平方
在网上看了看一些方法,一下摘自“风中落叶”hi.baidu.com/xiamengy
1.举例
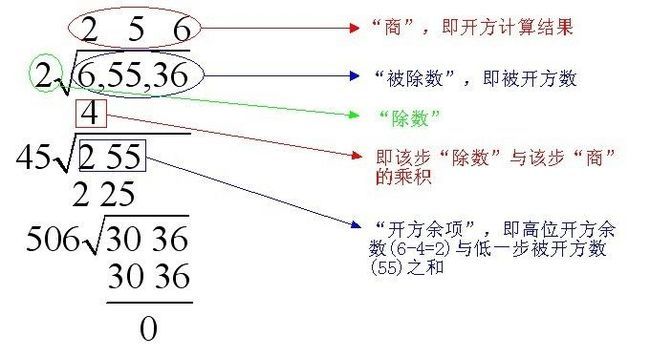
上式意为65536的开平方为256。手开方过程类似于除法计算。为了方便表述,以下仍称类似位置的数为“被除数”、“除数”、“商”。
以65536为例,其具体计算过程如下:
Step1:将被开方数(为了形象,表述成“被除数”,此例中即为65536)从个位往高位每两位一断写成6,55,35的形式,为了方便表述,以下每一个“,”称为一步
Step2:从高位开始计算开方。例如第一步为6,由于22=4<6<9=32,因此只能商2(这就是和除法不同的地方,“除数”和“商”的计算位必须相同)。于是将2写在根号上方,计算开方余项。即高位余项加一步低位,此例中,即为高位余项2和低位一步55,余项即为255。
Step3:将Step2得到的第一步开方得数2乘以20(原理在后面证明)作为第二步除数的高位。即本步除数是4x(四十几)。按照要求,本步的商必须是x。因为45×5=225<255<46×6=276,所以本步商5。
Step4:按照类似方法,继续计算以后的各步。其中,每一步的除数高位都是20×已求出的部分商。例如第三步的除数高位就是25×20=500,所以第三步除数为50x。本例中,506×6=3036恰好能整除,所以256就是最终计算结果。
2.字母表示和手开方公式的证明:
既然要证明,必须先把公式一般化。简言之,用字母而不是特殊值来表示计算过程和结果。
任意正整数均可表示成
则正整数M开方计算得到的就是A。根据手开方公式的思路,应该写成:
失一般性,对A进行推广。前面A表示正整数,现在A可以表示任意实数。因为计算开平方问题上,对于数值,正负是无所谓的。
因此不妨假设A为任意正实数。即可记
(即用科学计数法表示,例如134.87可以表示为
1.3487×102=(1+3×0.1+4×0.01+8×0.001+7×0.0001)×102)
如此,每一步的开方余项都用该步的“除数”和“商”表示出来,因此,手开方公式是精确的。
再进一步推广,对于更一般的情况,即使开方结果是无理数,或循环小数的,只需令n→∞即可。由于以上证明对任意n均成立,可以推得对于n→∞也相应成立。
上文的摘抄介绍了手开平方的方法以及证明,下面来说一下sgu111具体实现
这个我们主要其实是要解决“除数”
根据上文的证明可知,对于开平方,我们需要找到某个数(1~9),使得上一步的“商”×20+这个数,能尽可能地接近“开方余项”
设“这个数”为y,上一步的商为x
如上图的45=2*20+5
当(2*20+y)*y尽可能逼近255时,这个y可取。y=5时,(2*20+5)*5=225<255;y=6时,(2*20+6)*6=276>255,不符合,所以y取5
类似地,上图中的506也可以由(25*20+y)*y得到,只不过此时当y=6时,能正好取到3036
从高位求到低位的开方算法其实是取值范围的划定。
如果当前求当前位,设前面开好的一个大整数x,新数就是x*10+y,设当前的被开方数是a,必有:
a <= (x*10+y)2 = x2*100+20xy+y2 = x2+y*(20x+y)
根据这个算法的思想,我们要在上述不等式中使y求到最大,如果满足条件的情况下,y不是最大的,不论后面开出来的数有多大,结果都是有在x的数位前有很大的数字无法开尽,更谈不上逐步求解,缩小误差了。
具体实现:
首先我们给数字分位,要考虑奇数位的特殊情况。
一般的高精度a[1]是最低位,我这里反着存。
b[i-1]:=b[i-1]*2 这句话其实是b=20x
b[i]=j是b=20x+y
calc函数用来判断此时的y*(20x+y)能否取到最大值
Accepted Code
由于云昊哥最近旅游去了,所以...没人给我改C++的程序了....先用pascal写吧~
1 { 2 PROBLEM:sgu111 3 AUTHER:Rinyo 4 MEMO:手开平方 5 } 6 Program sgu111; 7 Const 8 Infile = 'sgu111.in'; 9 Outfile = 'sgu111.out'; 10 Var 11 a,b,c:Array[-1..1030]Of Longint; 12 len,i,j:Longint; 13 ch:Char; 14 Function calc(x,y:Longint):Boolean; 15 Var 16 t,i:Longint; 17 Begin 18 t:=0; 19 For i:=x DOwnto 0 DO Begin 20 c[i]:=b[i]*y+t; 21 t:=c[i] Div 10; 22 c[i]:=c[i] Mod 10; 23 End; 24 c[-1]:=t; 25 For i:=-1 To x Do 26 If c[i]>a[i+x] Then Begin 27 calc:=false; 28 Exit; 29 End Else If c[i]<a[i+x] Then Begin 30 calc:=true; 31 Exit; 32 End; 33 calc:=true; 34 ENd; 35 36 Begin 37 Assign(input,infile);Reset(input); 38 Assign(output,outfile);Rewrite(output); 39 Fillchar(a,sizeof(a),0); 40 Fillchar(b,sizeof(b),0); 41 len:=0; 42 While not eoln Do Begin 43 Inc(len);Read(ch);a[len]:=ord(ch)-ord('0'); 44 End; 45 If odd(len) Then Begin 46 For i:=len+1 Downto 1 Do a[i]:=a[i-1]; 47 Inc(len); 48 End; 49 For i:=1 To len Div 2 Do Begin 50 b[i-1]:=b[i-1]*2; 51 If b[i-1]>9 Then Begin b[i-1]:=b[i-1]-10;b[i-2]:=b[i-2]+1; End; 52 For j:=9 Downto 0 Do Begin 53 b[i]:=j; 54 If calc(i,j) Then Begin Write(j);break; End; 55 End; 56 For j:=i*2 Downto i-1 Do Begin 57 Dec(a[j],c[j-i]); 58 If a[j]<0 Then Begin Dec(a[j-1]);Inc(a[j],10); End; 59 End; 60 End; 61 WriteLn; 62 Close(input);Close(output); 63 End.