计算几何/sgu120 Arhipelago

题意

　　给出n，表示这是一个正n边形，并给出顺时针标号的n1,n2个点的坐标。输出所有点的坐标。

分析

　　计算几何。

　　主体思路：

　　　　利用n1,n2计算出这个正n边行的半径，进而求得中心坐标；

　　　　再利用向量旋转，从中心坐标开始，依次获得各个点坐标。

 

　　有关向量旋转参见百度文库http://wenku.baidu.com/view/3f95940cbb68a98271fefa75.html

　　主要用到的就是x1=x*cosθ-y*sinθ

　　　　　　　　　y1=x*sinθ+y*cosθ

 

     具体在程序中的变量以下图为例：

 

 

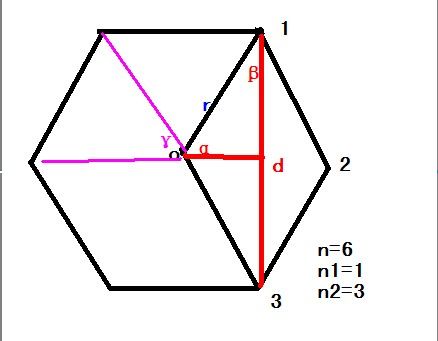
Accepted Code

 1 {

 2     PROBLEM:sgu120

 3     AUTHER:Rinyo

 4     MEMO:计算几何

 5 }

 6 

 7 

 8 Program sgu120;

 9 Const

10   Infile = 'sgu120.in';

11   Outfile = 'sgu120.out';

12 

13 Type

14   Rec = Record

15     x,y:Extended;

16   ENd;

17 

18 Var

19   p:Array[1..200]Of Rec;

20   alpha,beta,gamma,r,d:Extended;

21   n,n1,n2,i,k:Longint;

22   o:Rec;

23 

24 Function rotate(st,en:rec;deg,r:extended):rec;

25 Var

26   k,a:Rec;

27 Begin

28   k.x:=en.x-st.x;k.y:=en.y-st.y;

29   a.x:=r*k.x*cos(deg)-r*k.y*sin(deg)+st.x;

30   a.y:=r*k.x*sin(deg)+r*k.y*cos(deg)+st.y;

31   rotate:=a;

32 End;

33 

34 Begin

35   Assign(input,infile);Reset(input);

36   Assign(output,outfile);Rewrite(output);

37   ReadLn(n,n1,n2);

38   ReadLn(p[n1].x,p[n1].y);

39   ReadLn(p[n2].x,p[n2].y);

40 

41   alpha:=pi*(n2-n1)/n;

42   d:=sqrt(sqr(p[n1].x-p[n2].x)+sqr(p[n1].y-p[n2].y));

43   r:=d/(2*sin(alpha));

44 

45   beta:=pi/2-alpha;

46   o:=rotate(p[n2],p[n1],beta,1/(2*sin(alpha)));

47 

48   k:=n1;

49   gamma:=2*pi/n;

50 

51   Repeat

52     k:=(k+n-2) Mod n+1;

53     p[k]:=rotate(o,p[k mod n+1],gamma,1);

54   Until k=n1;

55   For i:=1 To n DO WriteLn(p[i].x:0:6,' ',p[i].y:0:6);

56   CLose(Input);Close(Output);

57 

58 End.