黎曼流形优化知识点学习
一、黎曼流形
切空间被赋予一个光滑变化的内积的流形就是黎曼流形Riemannian manifold。光滑变化的内积称为黎曼度量Riemannian metric。
二、线性空间,向量空间,矩阵空间
(一)线性空间
线性空间是一个抽象的数学概念,它是指一个集合,其中包含了元素和标量。这些元素之间可以进行加法运算和数乘运算,且仍得到元素。线性空间必须满足向量空间的所有条件,并且还需要满足以下条件:
- 加法交换律:u+v=v+u
- 加法结合律:(u+v)+w=u+(v+w)
- 加法单位元:存在一个元素 0∈V,使得 v+0=v
- 加法逆元:对于任意的 v∈V,存在一个元素 −v∈V,使得 v+(−v)=0
- 数乘结合律:α(βv)=(αβ)v
- 数乘单位元:1v=v
- 数乘分配律:(α+β)v=αv+βv
- 数乘分配律:α(u+v)=αu+αv
(二)向量空间
向量空间本质上是一个非空集合V,这个集合是由向量构成的,且该集合对加法和数乘(实数标量乘法)封闭,还需要包括零向量。
(三)矩阵空间
矩阵论——矩阵空间_浅夏琉殇的博客-CSDN博客
(四)线性空间,向量空间,矩阵空间的区别和联系
1、向量空间是线性空间的一种特殊情况,区别在于线性空间这个集合包含了元素和标量,而向量空间这个集合包含了向量和标量。
2、而矩阵空间是定义在数域 K 上的线性空间,其定义为矩阵空间 M 为 s×n 型矩阵构成的集合,矩阵之间存在加法运算和数乘运算,且仍得到 s×n 型矩阵。
三、回撤
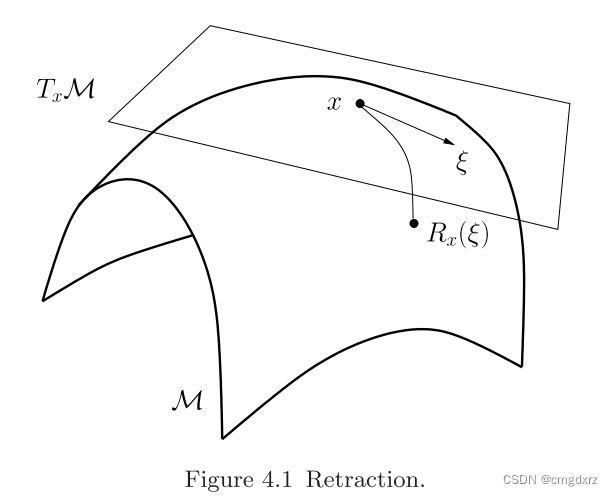
回撤(retraction)指的是从流形的切空间TxM到流形M本身的映射。具体来说,如果有一个黎曼流形M和它的一个点x,那么在x处的切空间就是所有在x处切于M的向量的集合。回撤映射就是描述如何从切空间TxM中的一个向量沿着某个方向移动到流形上的新点。
Rx(ξ)就表示在x点的切向量ξ从切空间回撤至流形的操作。
四、测地线,向量传输
(一)测地线
测地线(geodesic)是黎曼流形上两个点之间的最短测地线的长度。在直观的理解中,测地线可以被视为流形上的“匀速运动”(“加速度为0”)的轨迹。
在数学上,测地线的定义是流形上两个点之间最短的曲线。测地线的长度可以通过计算流形上两个点之间的距离来获得。这个距离可以用黎曼测度(Riemannian measure)来测量。
(二)向量传输
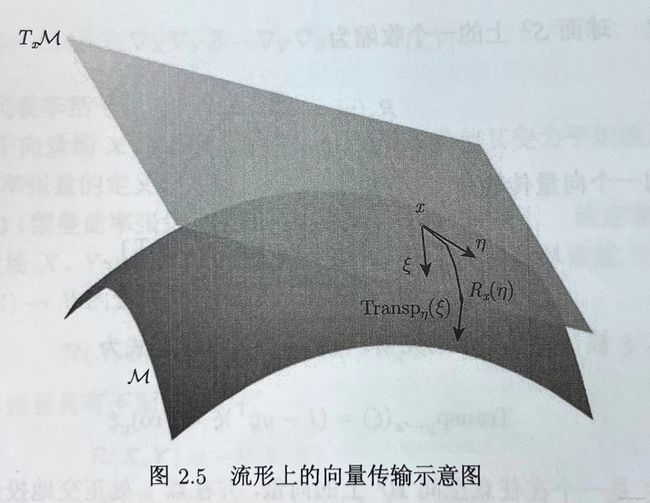
向量传输(vectoe transport)是平行移动(parallel translation)的近似。
向量传输的目的在于将一个向量ξ∈TxM从点x∈M移动至Rx(η)∈M(η∈TxM)。
五、指数映射,对数映射
(一)指数映射
在黎曼流形中,指数映射(Exponential Map)是一种从流形的切空间到流形本身的映射。
指数映射(Exponential Map)是这样一种映射:给定流形上的一个点x及相对应的切向量ξ,对x+ξ进行扩展。在欧式空间中,x+ξ在x点处沿着ξ的方向移动,移动距离为ξ。在黎曼流形中,给定流形上的一点x和x点的切空间中的一个切向量ξ,我们可以沿着x定义一条测地线。然后,指数映射将切向量ξ映射到沿着这条测地线行进一定距离后到达的点。这个距离通常取为1,即单位时间。其中测地线具有零加速度特性。对于一个具有黎曼联络的黎曼流形,移动的距离等于ξ的范数。
(另一种解释:在黎曼流形中,指数映射是一个从流形的切空间到流形本身的映射。具体来说,假设我们有一个n维完备的黎曼流形M,从M上任意一点p出发,选择任意一个切向量v,然后沿着这个切向量v作为参数的测地线,我们可以在测地线上截取长度为s的一段。这样,切向量v就被映射到了黎曼流形M上的一个点,这个点就是沿着测地线从点p出发,跑了长度s后到达的位置。这个映射过程就被称为黎曼流形M的指数映射。)
这个概念在微分几何和黎曼几何中非常重要,因为它提供了一种从切空间(局部)到流形(全局)的桥梁。通过指数映射,我们可以将局部的线性结构扩展到全局的非线性结构,从而研究和理解流形的复杂几何结构。 值得注意的是,虽然名字中有“指数”,但这并不意味着指数映射与指数函数有直接的关系。这个名字主要来自于李群和李代数中的指数映射,那里的指数映射确实与指数函数有关。但在一般的黎曼流形中,指数映射更多地是作为一种几何构造,而不涉及具体的指数运算。
(二)对数映射
在黎曼流形中,对数映射(Logarithmic Map)是指数映射的逆映射,只有在指数映射可逆的时候才存在。当给定一个起始点和目标点的情况下,对数映射将返回一个从指向的切向量,且有‖ x()‖ =dist(, )成立。
六、优化算法的全局收敛性
全局收敛性是优化算法的一个重要概念。如果从任意的初始点出发,算法产生的迭代点列都收敛到问题的最优值点,我们称该算法具有全局收敛性。这意味着无论我们从哪个点开始,我们都能找到问题的全局最优解。
相比之下,如果算法只有在初始点和最优值点具有某种程度的靠近时才能保证迭代点列收敛到最优值点,则称该算法具有局部收敛性。这意味着只有当我们从接近最优解的地方开始时,我们才能保证找到最优解。
总的来说,全局收敛性和局部收敛性是评价优化算法性能的重要指标,它们反映了算法在不同初始条件下寻找最优解的能力。在实际应用中,我们通常希望我们的优化算法具有良好的全局收敛性,这样我们就可以从任意初始点出发,通过迭代找到问题的全局最优解。但是,对于一些复杂的非凸问题,全局收敛可能很难实现,因此我们可能需要使用一些启发式方法或者结合先验信息来设计更有效的优化算法。
七、凸问题和非凸问题
如何判断函数凸或非凸? - 知乎