c语言一维数组

 一、一维数组的定义

  类型说明符 数组名 [常量表达式];

（一）类型说明符  --- 数据类型 

基本数据类型中 
       整型    int /short /long /long long 
       浮点型  float / double 
       字符型  char 
   其它的数据类型 --- 构造类型

（二）数组名 

    //一个名字 用来代表 这个数组 (一组相同类型变量 集合的一个名字)

（三）常量表达式

  []                       //就表示 数组 
 常量表达式      //整型的数值 --- 数组中元素的个数 ---数组长度

（四）说明

1.数组 本身也是一种数据类型 --- 构造类型 
  
2.识别数据类型   int a[30]    //去掉标识符 --剩下的就是标识符对应的数据类型 

3、发生数组越界的时候

      //编译器不检查

     //程序员自己小心
 

（五）数组的初始化

1、   int a[10] = {1,2,3,4,5,6,7,8,9,10};  //全部初始化 

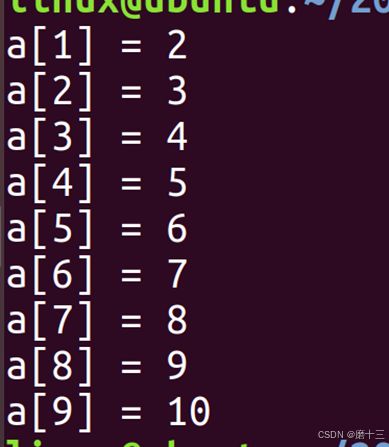
2、   int a[10] = {1,2,3,4,5,6}; //部分初始化 -- 前面依次给到，为初始化的部分默认初始化为0

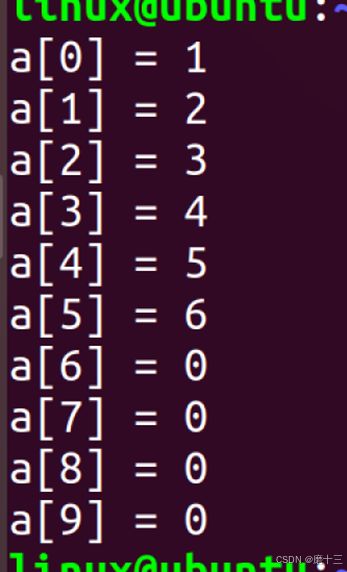
3、   int a[10] = {};  //数组初始化为0了   
4、   int a[10] = {0}; //数组初始化为0了
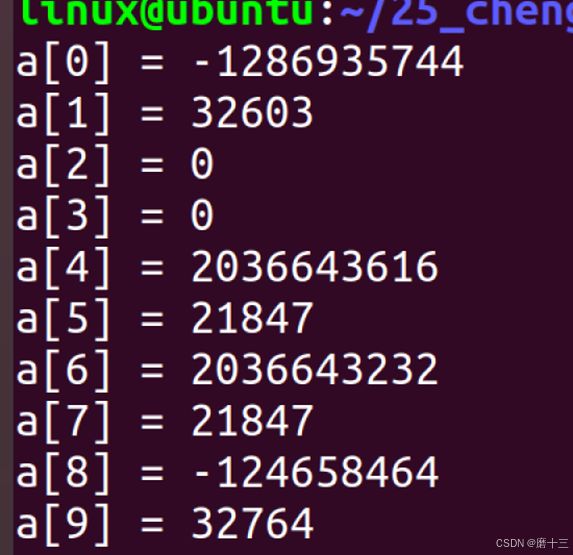
5、   int a[10] ; //为初始化 -- 数组中都是随机值 

（六）赋值、输入

赋值:
   数组不能整体操作 
   赋值只能挨个给到数组的元素

输入:
    数组不能整体操作 
    输入只能挨个给到数组的元素 

（七）内存空间

1、连续性

2、有序性

3、单一性

（八）数组的下标

  实际上是 偏移量 
  相对于首元素(地址)的偏移量

   N个元素取值范围是0~N-1.

二、实际运用

（一）选择排序   加二分法

代码如下：

#include

int main(void)
{
	int a[] = {2,4,3,1,5,11,8,6,14,10};//定义数组
	int len =sizeof(a) / sizeof(a[0]);//计算出数组的长度

	int j = 0;
    int i = 0;

	for(j = 0;j < len-1;j++)//j对应每个数的位置
	{
		for(i = j+1;i < len;i++)//i对应数字的下一个数字位置
		{
			if(a[i] < a[j])//判断它的下一位是否小于它
			{
			int n = a[j];//将这一位置的值给n
			a[j] = a[i];//将下一位数字的值给j的位置
			a[i] = n;//将j位置的值给下一位置的值
			}
		}
	}
#if 0
	for(j = 0;j < len;j++)
	{
	printf("%d ",a[j]);//循环打印j的值
	}
	printf("\n");
#endif

	int be = 0;
	int en = len -1;
	int mid = 0;
	int c;

	scanf("%d",&c);

	while(be <= en)
	{
		mid = ((be + en) /2);
		if(a[mid] > c)
		{
			en = mid -1;
		}else if(a[mid] < c)
		{
			be = mid +1;
		}else
		{
			printf("找到了\n");
			break;
		}

	}
	if(be > en)
	{
		printf("没找到\n");
	}



	return 0;
}

（二）冒泡排序

#include

int main(void)
{
	int a[] = {5,2,6,7,1,9,35,8};
	int len = sizeof(a) / sizeof(a[0]);

	int i = 0;
	int j = 0;
	int n;

	for(j = 1;j < len;j++)//控制比较的趟数
	{
		for(i = 0;i < len-j;i++)//控制一趟比较的次数
		{
			if(a[i] > a[i+1])//判断这一位数是否比下一位数大
			{
				 n = a[i];//交换
				a[i] = a[i+1];
				a[i+1] = n;
			}
		}
	}

	for(i = 0;i < len;i++)//i，j的值无所谓
	{
		printf("%d ",a[i]);
	}
	printf("\n");

	return 0;
}

（三）逆序输出

#include

int main(void)
{
	int a[] = {1,2,3,4,5,6,7,8,9,10};
	int len = sizeof(a) / sizeof(a[0]);
	int n;

	int i = 0;
	int j = 0;

	for(i = 0,j = len-1;i < j;i++,j--)
	{
		n = a[i];
		a[i] = a[j];
		a[j] = n;
	}
#if 0
	for(i=0;i

（四）寻找最大值

#include

int main(void)
{
	int	nmax = 0x80000000;
	int a[] = {150,42,39,45,51,6,8,5,9,10};
	int len = sizeof(a) / sizeof(int);
	int max = a[0];

	int i;
	for(i=1;i < len;i++)
	{
		if(a[i] > max)//找出最大值
		{
			max = a[i];
		}
	}
	for(i=0;i< len;i++)
	{
		if(a[i] > nmax && a[i] < max)//过滤最大值
			nmax = a[i];
	}

	printf("%d\n",max);
	printf("%d\n",nmax);


	return 0;

}

 （五）时间复杂度

      判断算法好坏?

       计算时间复杂度的基本步骤

1. ‌找出算法中的基本语句‌：算法中执行次数最多的那条语句就是基本语句，通常是最内层循环的循环体。‌1

2. ‌计算基本语句的执行次数的数量级‌：只需保留f(n)中的最高次幂，可以忽略所有低次幂和最高次幂的系数。

3. ‌用大O记号表示算法的时间性能‌：将基本语句执行次数的数量级放入大O记号中。