Day25 非递减子序列 全排列 全排列 II

回溯算法 part04

491. 非递减子序列 - 力扣（LeetCode）

超时 是因为res.contains(path) 耗时

先搜索所有结果 之后判断结果是否有序

    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> res =new ArrayList<>();
//    先搜索所有结果 之后判断结果是否有序
     public List<List<Integer>> findSubsequences(int[] nums) {
         backTracking(nums,0);
         return res;
    }
    void backTracking(int[] nums,int startIndex){
         if(path.size() > nums.length){
             return;
         }
        Boolean sorted = isSorted(path);
        if(!res.contains(path)&&sorted&&path.size()>=2){
             res.add(new ArrayList<>(path));
         }
         for(int i = startIndex;i< nums.length;i++){
             path.add(nums[i]);
             backTracking(nums,i+1);
             path.removeLast();
         }
    }
    Boolean isSorted(List<Integer> list){
         int flag =0;
         for(int i=0;i<list.size();i++){
             if(i>0&&list.get(i)<list.get(i-1)){
                 flag =1;
                 break;
             }
         }
         if(flag == 1){
             return false;
         }else {
             return true;
         }
    }

解决超时 就要更改去重方式 用if(i>startIndex&&nums[i] == nums[i-1])

但是又 踩坑了 上述比较去重 只能比较相邻元素之间是否有重复 前提是将nums排序

但是但是，不能先排序，问题是求原数组中的递增序列 所以要用set集合来去重（4757）后面7要剪枝

    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> res =new ArrayList<>();
//    先搜索所有结果 之后判断结果是否有序
     public List<List<Integer>> findSubsequences(int[] nums) {
         backTracking(nums,0);
         return res;
    }
    void backTracking(int[] nums,int startIndex){
//         递归终止条件 path.size()> nums.length 可省略
        Boolean sorted = isSorted(path);
        if(sorted&&path.size()>=2){
             res.add(new ArrayList<>(path));
         }
//        只搜集同一树层的结果
        HashSet<Integer> set = new HashSet<>();
        for(int i = startIndex;i< nums.length;i++){
//             path.size()>0&&path.get(path.size()-1)>nums[i] 也可以判断是否递增
//             i>startIndex&&nums[i]==nums[i-1] 不能用在此题的树层去重. 7574不是相邻元素之间的去重 要用set
             if(set.contains(nums[i])){
                 continue;
             }
             set.add(nums[i]);
             path.add(nums[i]);
             backTracking(nums,i+1);
             path.removeLast();
         }
    }
    Boolean isSorted(List<Integer> list){
         int flag =0;
         for(int i=0;i<list.size();i++){
             if(i>0&&list.get(i)<list.get(i-1)){
                 flag =1;
                 break;
             }
         }
         if(flag == 1){
             return false;
         }else {
             return true;
         }
    }

优化 path.size()>0&&path.get(path.size()-1)>nums[i] 也可以判断是否递增

    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> res =new ArrayList<>();
//    先搜索所有结果 之后判断结果是否有序
     public List<List<Integer>> findSubsequences(int[] nums) {
         backTracking(nums,0);
         return res;
    }
    void backTracking(int[] nums,int startIndex){
//         递归终止条件 path.size()> nums.length 可省略
//        Boolean sorted = isSorted(path);
        if(path.size()>=2){
             res.add(new ArrayList<>(path));
         }
//        只搜集同一树层的结果
        HashSet<Integer> set = new HashSet<>();
        for(int i = startIndex;i< nums.length;i++){
//             i>startIndex&&nums[i]==nums[i-1] 不能用在此题的树层去重. 7574不是相邻元素之间的去重 要用set
             if(set.contains(nums[i])||path.size()>0&&path.get(path.size()-1)>nums[i]){
                 continue;
             }
             set.add(nums[i]);
             path.add(nums[i]);
             backTracking(nums,i+1);
             path.removeLast();
         }
    }

46. 全排列 - 力扣（LeetCode）

同一树枝上不能出现重复元素 可以通过path.contains(nums[i])判断

LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> res =new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
    backTracking(nums);
    return res;
}
void backTracking(int[] nums){
    if(path.size() == nums.length){
        res.add(new ArrayList<>(path));
        return;
    }
    for(int i=0;i<nums.length;i++){
        if(path.contains(nums[i])){
            continue;
        }
        path.add(nums[i]);
        backTracking(nums);
        path.removeLast();
    }
}

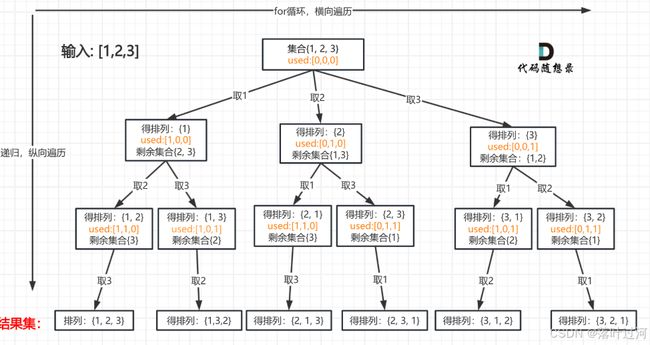
用 boolean[] used;记录是否被使用 注意回溯设为false used和path树枝去重的区别是 前者记录的是索引值可以标记数值相同的数

boolean[] used;
LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> res =new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
    used=new boolean[nums.length];
    for (int i=0;i<used.length;i++){
        used[i] = false;
    }
    backTracking(nums);
    return res;
}
void backTracking(int[] nums){
    if(path.size() == nums.length){
        res.add(new ArrayList<>(path));
        return;
    }
    for(int i=0;i<nums.length;i++){
        if(used[i]){
            continue;
        }
        used[i] =true;
        path.add(nums[i]);
        backTracking(nums);
        path.removeLast();
        used[i] =false;
    }
}

47. 全排列 II - 力扣（LeetCode）

同一树层（set）和 同一树枝 (used)都要去重

boolean[] used;
LinkedList<Integer> path = new LinkedList<>();
List<List<Integer>> res =new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
    used=new boolean[nums.length];
    for (int i=0;i<used.length;i++){
        used[i] = false;
    }
    backTracking(nums);
    return res;
}
void backTracking(int[] nums){
    if(path.size() == nums.length){
        res.add(new ArrayList<>(path));
        return;
    }
    HashSet<Integer> set = new HashSet<>();
    for(int i=0;i<nums.length;i++){
//        同一树层和 同一树枝 都要去重
        if(used[i]||set.contains(nums[i])){
            continue;
        }
        set.add(nums[i]);
        used[i] =true;
        path.add(nums[i]);
        backTracking(nums);
        path.removeLast();
        used[i] =false;
    }
}

回溯问题 就是

树枝(path or used) 树层处理(set去重 或者 i>startIndex&&nums[i]==nums[i-1])

如何剪枝 （for中对i约束 或者 判断break） 去重（相邻元素之间去重，不相邻6787）剪枝

组合与排列（used或者path.contains(nums[i]） （是取所有节点（子集） 还是叶子节点）

注意源集合是否有重复元素【224546】结果是否可重复

startIndex是否要加1去重