计算扇形与圆的交点
效果图:
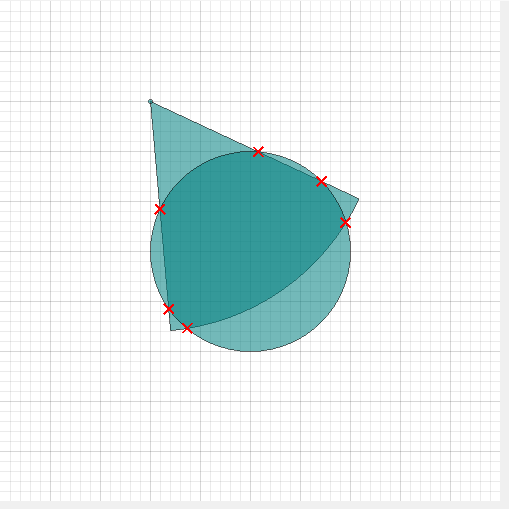

算法:
基本思路是检测圆和圆的交点,检测扇形边和圆的交点,其中圆和圆的交点还要判断点是否在扇形的角度内部。判断方法参考:
http://stackoverflow.com/questions/13652518/efficiently-find-points-inside-a-circle-sector
交点判断方法可以看之前的博客

internal class MathEx { /// <summary> /// 浮点类型的精度要求 /// </summary> public const float EPS = 0.00001f; /// <summary> /// 线段与圆的交点 /// </summary> /// <param name="ptStart">线段起点</param> /// <param name="ptEnd">线段终点</param> /// <param name="ptCenter">圆心坐标</param> /// <param name="Radius">圆半径</param> /// <param name="ptInter1">交点1(若不存在返回65536)</param> /// <param name="ptInter2">交点2(若不存在返回65536)</param> public static bool LineInterCircle(PointF ptStart, PointF ptEnd, PointF ptCenter, double Radius, ref PointF ptInter1, ref PointF ptInter2) { double Radius2 = Radius*Radius; ptInter1.X = ptInter2.X = 65536.0f; ptInter1.Y = ptInter2.Y = 65536.0f; var fDis = (float) Math.Sqrt((ptEnd.X - ptStart.X)*(ptEnd.X - ptStart.X) + (ptEnd.Y - ptStart.Y)*(ptEnd.Y - ptStart.Y)); var d = new PointF(); d.X = (ptEnd.X - ptStart.X)/fDis; d.Y = (ptEnd.Y - ptStart.Y)/fDis; var E = new PointF(); E.X = ptCenter.X - ptStart.X; E.Y = ptCenter.Y - ptStart.Y; float a = E.X*d.X + E.Y*d.Y; float a2 = a*a; float e2 = E.X*E.X + E.Y*E.Y; if ((Radius2 - e2 + a2) < 0) { return false; } else { var f = (float) Math.Sqrt(Radius2 - e2 + a2); float t = a - f; if (((t - 0.0) > -EPS) && (t - fDis) < EPS) { ptInter1.X = ptStart.X + t*d.X; ptInter1.Y = ptStart.Y + t*d.Y; } t = a + f; if (((t - 0.0) > -EPS) && (t - fDis) < EPS) { ptInter2.X = ptStart.X + t*d.X; ptInter2.Y = ptStart.Y + t*d.Y; } return true; } } /// <summary> /// 以中心点逆时针旋转Angle角度 /// </summary> /// <param name="center">中心点</param> /// <param name="p1">待旋转的点</param> /// <param name="angle">旋转角度(弧度)</param> public static PointF PointRotate(PointF center, PointF p1, double angle) { double x1 = (p1.X - center.X)*Math.Cos(angle) + (p1.Y - center.Y)*Math.Sin(angle) + center.X; double y1 = -(p1.X - center.X)*Math.Sin(angle) + (p1.Y - center.Y)*Math.Cos(angle) + center.Y; return new PointF((float) x1, (float) y1); } /// <summary> /// 判断两个平行于x轴的圆的交点 /// </summary> /// <param name="centerA">第一个圆的中点</param> /// <param name="rA">半径</param> /// <param name="centerB">第二个圆的中点</param> /// <param name="rB">半径</param> /// <param name="ptInter1">交点1(若不存在返回65536)</param> /// <param name="ptInter2">交点1(若不存在返回65536)</param> public static void CircleInterCircleOnXAxis(PointF centerA, double rA, PointF centerB, double rB, ref PointF ptInter1, ref PointF ptInter2) { ptInter1.X = ptInter2.X = 65536.0f; ptInter1.Y = ptInter2.Y = 65536.0f; PointF centerLeft; double R, r, d; if (centerA.X < centerB.X) { centerLeft = centerA; R = rA; r = rB; d = centerB.X - centerA.X; } else { centerLeft = centerB; R = rB; r = rA; d = centerA.X - centerB.X; } double R2 = R*R; double x = (d*d - r*r + R2)/(2*d); double y = Math.Sqrt(R2 - x*x); ptInter1.X = centerLeft.X + (int) x; ptInter1.Y = centerLeft.Y + (int) y; ptInter2.X = centerLeft.X + (int) x; ptInter2.Y = centerLeft.Y - (int) y; } /// <summary> /// 求任意两个圆的交点 /// </summary> /// <param name="centerA">第一个圆的中点</param> /// <param name="rA">半径</param> /// <param name="centerB">第二个圆的中点</param> /// <param name="rB">半径</param> /// <param name="ptInter1">交点1(若不存在返回65536)</param> /// <param name="ptInter2">交点1(若不存在返回65536)</param> public static void CircleInterCircle(PointF centerA, double rA, PointF centerB, double rB, ref PointF ptInter1, ref PointF ptInter2) { var v = new PointF(centerB.X - centerA.X, centerB.Y - centerA.Y); double angle = GetAngleWithXAxis(v); PointF bb = PointRotate(centerA, centerB, angle); PointF p1 = Point.Empty, p2 = Point.Empty; CircleInterCircleOnXAxis(centerA, rA, bb, rB, ref p1, ref p2); if (!Equal(p1.X, 65536.0f)) { p1 = PointRotate(centerA, p1, -angle); } if (!Equal(p2.X, 65536.0f)) { p2 = PointRotate(centerA, p2, -angle); } ptInter1 = p1; ptInter2 = p2; } /// <summary> /// 计算两个向量的夹角 /// </summary> /// <param name="Va"></param> /// <param name="Vb"></param> /// <returns></returns> public static float GetAngleOfVectors(PointF Va, PointF Vb) { var da = (float) Math.Sqrt(Va.X*Va.X + Va.Y*Va.Y); var db = (float) Math.Sqrt(Vb.X*Vb.X + Vb.Y*Vb.Y); var theta = (float) Math.Acos((Va.X*Vb.X + Va.Y*Vb.Y)/(da*db)); return theta; } /// <summary> /// 计算向量与x轴正方形的夹角 /// </summary> /// <param name="V"></param> /// <returns>(0~360)</returns> public static double GetAngleWithXAxis(PointF V) { double theta = GetFov(new PointF(0, 0), V)*Math.PI/180; return theta; } public static bool Equal(double a, double b) { return Math.Abs(a - b) < EPS; } public static List<PointF> SectorInterCircle(PointF centerS, float rS, float fov, float angle, PointF centerC, float rC) { double angleC2 = angle/2; PointF Na = GetPointFovTo(new PointF(0,0), fov - angleC2, 1); PointF Nb = GetPointFovTo(new PointF(0, 0), fov + angleC2, 1); PointF a = new PointF(Na.X*rS+centerS.X,Na.Y*rS+centerS.Y); PointF b = new PointF(Nb.X * rS + centerS.X, Nb.Y * rS + centerS.Y); var list = new List<PointF>(); PointF p1 = PointF.Empty, p2 = PointF.Empty; LineInterCircle(centerS, a, centerC, rC, ref p1, ref p2); if (!Equal(p1.X, 65536.0f)) { list.Add(new PointF(p1.X, p1.Y)); } if (!Equal(p2.X, 65536.0f)) { list.Add(new PointF(p2.X, p2.Y)); } p1 = PointF.Empty; p2 = PointF.Empty; LineInterCircle(centerS, b, centerC, rC, ref p1, ref p2); if (!Equal(p1.X, 65536.0f)) { list.Add(new PointF(p1.X, p1.Y)); } if (!Equal(p2.X, 65536.0f)) { list.Add(new PointF(p2.X, p2.Y)); } p1 = PointF.Empty; p2 = PointF.Empty; CircleInterCircle(centerS, rS, centerC, rC, ref p1, ref p2); if (!Equal(p1.X, 65536.0f) && !areClockwise(Na, new PointF(p1.X - centerS.X, p1.Y - centerS.Y)) && areClockwise(Nb, new PointF(p1.X - centerS.X, p1.Y - centerS.Y))) { list.Add(new PointF(p1.X, p1.Y)); } if (!Equal(p2.X, 65536.0f) && !areClockwise(Na, new PointF(p2.X - centerS.X, p2.Y - centerS.Y)) && areClockwise(Nb, new PointF(p2.X - centerS.X, p2.Y - centerS.Y))) { list.Add(new PointF(p2.X, p2.Y)); } return list; } private static bool areClockwise(PointF v1, PointF v2) { return -v1.X*v2.Y + v1.Y*v2.X > 0; } public static float Distance(PointF a, PointF b) { return (float)Math.Sqrt((a.X - b.X) * (a.X - b.X) + (a.Y - b.Y) * (a.Y - b.Y)); } /// <summary> /// 已知点a,和方向arf(0-360),求点a,arf方向上距离为L的点坐标 /// </summary> /// <param name="s"></param> /// <param name="arf"></param> /// <param name="l"></param> /// <returns></returns> public static PointF GetPointFovTo(PointF s, double arf, double l) { while (arf < 0) arf += 360; while (arf >= 360) arf -= 360; if (arf >= 0 && arf < 90) { double angle = arf*Math.PI/180; return new PointF((float) (s.X + l*Math.Cos(angle)), (float) (s.Y + l*Math.Sin(angle))); } else if (arf >= 90 && arf < 180) { double r = 180 - arf; double angle = r*Math.PI/180; return new PointF((float) (s.X - l*Math.Cos(angle)), (float) (s.Y + l*Math.Sin(angle))); } else if (arf >= 180 && arf < 270) { double r = 270 - arf; double angle = r*Math.PI/180; return new PointF((float) (s.X - l*Math.Sin(angle)), (float) (s.Y - l*Math.Cos(angle))); } else if (arf >= 270 && arf < 360) { double r = 360 - arf; double angle = r*Math.PI/180; return new PointF((float) (s.X + l*Math.Cos(angle)), (float) (s.Y - l*Math.Sin(angle))); } return PointF.Empty; } /// <summary> /// 已知两个点a,b求射线ab的方向 /// </summary> /// <param name="a"></param> /// <param name="b"></param> /// <returns></returns> public static float GetFov(PointF a, PointF b) { if (a.X == b.X) { if (a.Y >= b.Y) return 270; else return 90; } else if (a.Y == b.Y) { if (a.X < b.X) return 0; else return 180; } else { double Xab = b.X - a.X; double Yab = b.Y - a.Y; double Rab = Math.Atan(Math.Abs(Xab)/Math.Abs(Yab)); Rab = Rab*(180/Math.PI); if (Xab > 0 && Yab >= 0) return (float) (450 - Rab)%360; if (Xab < 0 && Yab >= 0) return (float) (450 + Rab)%360; if (Xab < 0 && Yab <= 0) return (float) (630 - Rab)%360; if (Xab > 0 && Yab <= 0) return (float) (Rab + 270)%360; } return 0; // var p = new PointF(b.X - a.X, b.Y - a.Y); // return (float)(GetAngleOfVectors(p, new PointF(1, 0))*180/Math.PI); } }
