9、深度学习-自学之路-损失函数、梯度下降、学习率、权重更新的理解

由《8、深度学习-自学之路-损失函数和梯度下降程序展示》我们看到我们设计了一个程序，这个程序里面由学习率，有损失函数，有梯度下降，权重更新。

一、我们先来讲一下损失函数，

e_dn = (p_dn - ture)**2 #损失值的计算

p_dn：预测值

ture：真实值

e_dn：损失值

我们在第7章说了，我们的预测值和真实值相差越小（也就是损失值越小），说明我们模型训练的越好。这个也是我们进行模型训练的原因。

我们使用了最小二乘法来做我们的损失函数的原因（当然还有很多其他的损失函数可以用，我们现在先把最小二乘法这个讲明白，后面的其他的损失函数都是一样的理解。自己学习就行，实在不行后面我再出一篇对应的文章来讲解不同损失函数的应用），

第一是：因为损失值不能是负值和正值来回跳动，不让不好对模型进行评估。

第二是：如果预测值和真实值偏差大，那么平方之后，这个值就更大了。那么在下次权重更新中，会加快这个值的更新。让预测值和真实值之间差距减小。如果预测值和真实值偏差小，那么平方后，这个值就更小了。这样在权重更新时就会减慢更新，防止震荡的发生。

二、我们来说一下梯度下降，以及为什么要这么下降。

weight = weight - lr*input*(p_dn - ture) #进行权重的梯度下降

weight：权重值

lr：学习率

input：输入值

p_dn - ture：预测值和真实值的偏差。

我们用程序证明了，我们权重这么更新是很有用的。但是我们不知道为什么要这么做。这里我来讲一下我的理解。

我们还是要从损失函数讲起：

e_dn = (p_dn - ture)**2

p_dn=prediction = input*weight

e_dn = (input*weight- ture)**2

在e_dn = (input*weight- ture)**2这个公式中，我们的输入是已知的，真实值也是已知的，然后我们损失函数就可以写成是e_dn关于weight的函数。

e_dn=（input*weight-ture）**2

化简后得到：e_dn =input*input* weight - 2*input*weight*weight+weight*weight；

我们把e_dn=y

把weight=x

把input*input= a

把2*input*weight=b

把weight*weight=c

原公式可以化简为：y = a*x*x-b*x+c;

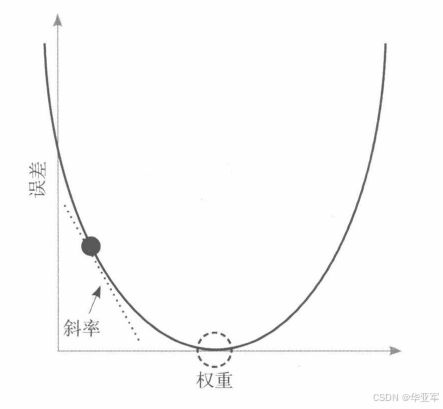
根据我们学过的知识：我们知道y = a*x*x-b*x+c;是一个开口向上的U型

如果所示：当权重值在最低端的时候，Y=0,损失值最小，是我们想要达到的点。

那么我们怎么让权重的更新来达到损失之最小的点呢，那么就要引入梯度下降

在我们大脑识别一个新的事物和新的知识的时候，我们大脑中的权重是一片模糊的，是混沌的状态，经过很多次训练之后，我们在我们的大脑中得到了一个最完美的权重，这个权重可以让我们每次观察我们已经学习到的内容时，损失值最小。

在我们最开始要进行训练的时候，我们的权重值是一个未知的，可以在整个U型曲线上的任意一点，可以是最左边的点，也可以是最右边的点，也可能是最低点。但是大概率我们的最初值不会落在最低点，概率上的问题。所以我们学习的时候肯定会经历这种梯度下降的情况。

那么我们怎么让权重最快的到达我们的U行的最低点呢，这就要引入导数的概念，导数是图形上的一个点上，下降最快的点。下降最快的值是导数，是下降还是上升取决于导数的符号，导数是正上升，导数是负就下降。这个里面也可以叫收敛。

e_dn=（input*weight-ture）**2的导数为2*（input*weight-ture）也可以写作2*(p_dn - ture)

然后看一下我们的权重更新的公式为：

weight = weight - lr*input*(p_dn - ture) #进行权重的梯度下降

这这个式子中：

weight：是权重

lr：是学习率，后面我们会讲。

input：是输入值。大家也会说为什么要把输入值也放到这个式子中来呢，这个是因为，这个权重是对应这个输入的更新。目前《8、深度学习-自学之路-损失函数和梯度下降程序展示》里面我们只有一个输入元素。为的是让大家能够手算理解这整个的过程。因为多输入会加大我们的计算量，同时也会增加计算的复杂程度。一个输入理解了，多个输入只是比这个复杂一点而已。但是多个输入的时候，在权重更新的时候，就要针对相应的输入进行更新，要不然所有的权重最后都是一个值，那就不能完成模型的建立。

(p_dn - ture)：梯度下降的对应梯度值。这里大家会说为什么不是2*(p_dn - ture)，这个其实是没有关系的，有2的系数，跑的更快，没有2这个系数，跑的慢一点。这个后面的学习率的时候我们会说明一下。

三：学习率lr

一直发现程序中会有lr这个值，但是大家可能都在想这个值的意义；

这个学习率其实和我们的模型的学习时间是有关系的，这个值越大，我们的损失值越会快速的降低到最小值，

但是也有一个问题，如果这个值太大，在损失值到达最低点的时候，我们可能导致损失值在最低点左右摇摆，

如果这个学习率太大，也可能导致损失之回不到最低点。

那么学习率是不是越小越好呢，也不是，如果学习率太小，那么到达损失值最低点的时候，要花费很多时间，经过很多次运算。这样虽然效果好，但是时间成本上太长时间我们接受不了。

所以这个学习率需要我们一步一步的尝试着来设置，一般的设置规则是1 0.1 0.01 0.001.按照这种10倍乘来设置，然后观察损失值是否能够快速的降低到最小值。

四：权重更新，其实在梯度下降中已经讲了权重的更新了，权重的更新就是为了让损失函数快速降低到最小值。