算法-数组篇04-长度最小的子字符串

长度最小的子字符串

力扣题目链接

题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

滑动窗口

和双指针方法类似，给定一个长度l，在数组中依次遍历0到l，1到l+1…,r到r+l。利用这个方法可以求解数组中一些子字符串的问题。

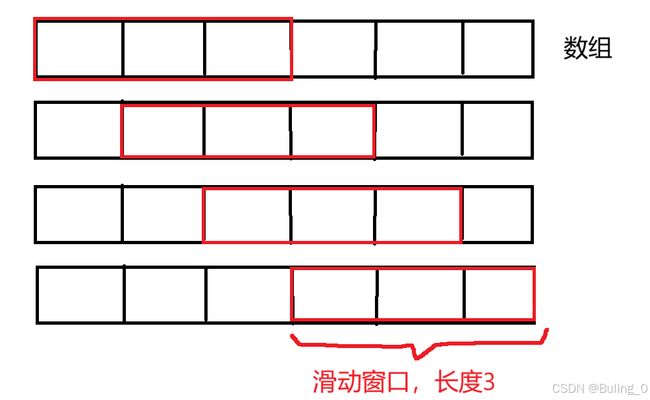
解题思路

首先看到这道题目的第一想法自然是使用滑动窗口暴力求解，先固定滑动窗口的长度，然后使用滑动窗口遍历数组。遍历完成后窗口大小加一，直至当滑动窗口内的数据之和大于target时返回滑动窗口的长度，或者窗口大小等于数组大小，此时说明数组总和仍小于target，那么返回0。

class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int n = nums.size();
        for(int i = 1; i <= n; i++){
            for(int j = 0; j <= n - i; j++){
                int m = 0;
                for(int k = j; k < j + i; k++){
                    m += nums[k];
                }
                if(m >= target){
                    return i;
                }
            }
        }

        return 0;
    }
};

但是在写完暴力求解的方法后，发现该解法超时。
通过分析，我们可以发现，提示中：
1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁴
说明解法要求的时间复杂度是O(n²)
而我们的解法很明显是O(n³)
那么我们需要继续优化我们的算法。

题解

暴力解法

时间复杂度：O(n²)
优化：我们的算法复杂度是O(1)到O(n³)，取决于数组中是否含有子数组，以及其位置。早发现早返回。那么我们可以想到直接遍历每个位置不同长度的窗口，一旦发现直接返回这个位置最小的窗口，那么可以将复杂度降为O(n²)。

class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int n = nums.size();
        int ans = 0, l = 0;
        for(int i = 0; i < n; i++){
            int sum = 0;
            for(int j = i; j < n; j++){
                sum += nums[j];
                if(sum >= target){
                    l = j - i + 1;
                    if(ans == 0){
                        ans = l;
                    }
                    else {
                        ans = ans < l ? ans : l;
                    }
                    break;
                }
            }
        }

        return ans;
    }
};

这个解法虽然把复杂度降到了O(n²)，但是不清楚为什么还是无法通过，一直是显示超出时间限制，然后我试了一下官方解法，结果发现官方暴力解法也是超时(什么乐子)。反复分析了一下，暴力解法是没有问题的，理论上复杂度也是在要求内的。

优化后的滑动窗口(最优解)

时间复杂度：O(n)
这个解法是查看题解后学废的。(但是我感觉这个不能算是滑动窗口，应该是我的问题)
总体思路是：
从一开始向后去增大滑动窗口，直到窗口内值大于target，此时将flag置为true说明存在解，然后从前方缩小窗口。然后重复这个过程，并和ans比较大小，遍历一遍下来，可以保证ans是最小的解。最后判断flag是否存在解。

class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int l = nums.size();
        int p = 0, ans = l, sum = nums[0];
        bool flag = false;

        for(int i = 0; p < l; ){
            if(sum < target && i < l - 1){
                i++;
                sum += nums[i];
            }
            else if(sum < target && i == l - 1){
                break;
            }
            else{
                int temp = i - p + 1;
                ans = ans < temp ? ans : temp;
                sum -= nums[p];
                p++;
                flag = true;
            }
        }
        if(ans == l && flag == false){
            ans = 0;
        }

        return ans;

    }
};

前缀和 + 二分法

时间复杂度：O(n log(n))
这个解法我觉得非常巧妙。这里我就直接复制答案的描述了。

---

为了使用二分查找，需要额外创建一个数组 sums 用于存储数组 nums 的前缀和，其中 sums[i] 表示从 nums[0] 到 nums[i−1] 的元素和。得到前缀和之后，对于每个开始下标 i，可通过二分查找得到大于或等于 i 的最小下标 bound，使得 sums[bound]−sums[i−1]≥s，并更新子数组的最小长度（此时子数组的长度是 bound−(i−1)）。

因为这道题保证了数组中每个元素都为正，所以前缀和一定是递增的，这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正，这里就不能使用二分来查找这个位置了。

作者：力扣官方题解
链接：https://leetcode.cn/problems/minimum-size-subarray-sum/solutions/305704/chang-du-zui-xiao-de-zi-shu-zu-by-leetcode-solutio/
来源：力扣（LeetCode）

---

class Solution {
public:
    int minSubArrayLen(int s, vector& nums) {
        int n = nums.size();
        if (n == 0) {
            return 0;
        }
        int ans = INT_MAX;
        vector sums(n + 1, 0); 
        // 为了方便计算，令 size = n + 1 
        // sums[0] = 0 意味着前 0 个元素的前缀和为 0
        // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
        // 以此类推
        for (int i = 1; i <= n; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
        for (int i = 1; i <= n; i++) {
            int target = s + sums[i - 1];
            auto bound = lower_bound(sums.begin(), sums.end(), target);
            if (bound != sums.end()) {
                ans = min(ans, static_cast((bound - sums.begin()) - (i - 1)));
            }
        }
        return ans == INT_MAX ? 0 : ans;
    }
};

总结

这道题使用暴力解法还是比较简单的，但是官方的暴力解法也会显示超时，说明这道题还是希望我们使用后面两种方法的，这里的滑动窗口的使用是十分巧妙的一种方法，通过增长和缩短来去寻找最优解。而前缀和+二分查找的方法虽然在效率上差了一些，但是仍不为一种十分好用的方法。