二叉树的遍历和增删改查-2

二叉树结点的个数

对于二叉树的结点个数我们采用的递归的方式去实现，主要的思路就是遇到null就返回0，如果不是空结点，我们就返回1.再完成左右子树的递归之后，它的总数会作为结果返回。所以这个函数的声明是这样的、

int binarytreesizebata(BinraryTreeNode* root)

再这里我们以前序遍历做演示

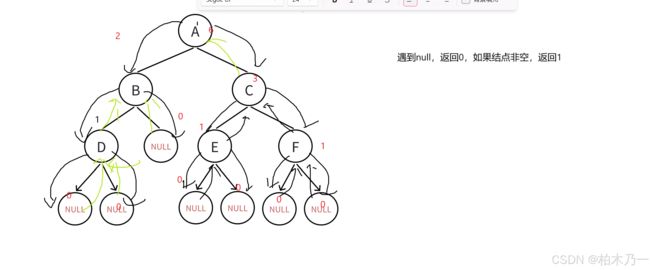
具体代码如下，具体遍历规则如同前序遍历一样

int binarytreesizebata(BinraryTreeNode* root)
{

	if (root == NULL)
	{
		return 0;
	}
	return 1 + binarytreesizebata(root->left) + binarytreesizebata(root->right);
}

总结点=根节点个数+左子树结点个数+右子树结点个数
而左右子树结点也是一颗单独的子树，具体细分也可以变成，总结点=根节点个数+左子树结点个数+右子树结点个数。

二叉树叶子结点个数

所谓的叶子结点就是二叉树度位0的结点，在它之下没有其他的结点了。因为这个二叉树是递归树，我们依旧采用递归的形式。在这里仍然以先序遍历作为演示。
叶子结点因为度为0的缘故，它的左右结点都为空，这是它的主要特征。
所谓在这里
有两个结束条件
1.该结点等于空，我们返回0.
2.该结点的左右结点均为空，我们返回1，证明这是一个叶子结点

返回结果是，左子树的叶子结点个数+右子树的叶子结点的叶子个数、

int binarytreeleafsize(BinraryTreeNode* root);

如果这个二叉树只有第一次有结点，也就是只有一个根节点，它会在第二个返回条件直接返回，不会进入到下面的递归环节。
因为该方法用图和字的方式不好解释具体过程，在这里只提供代码

int binarytreeleafsize(BinraryTreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return binarytreeleafsize(root->left) + binarytreeleafsize(root->right);


}

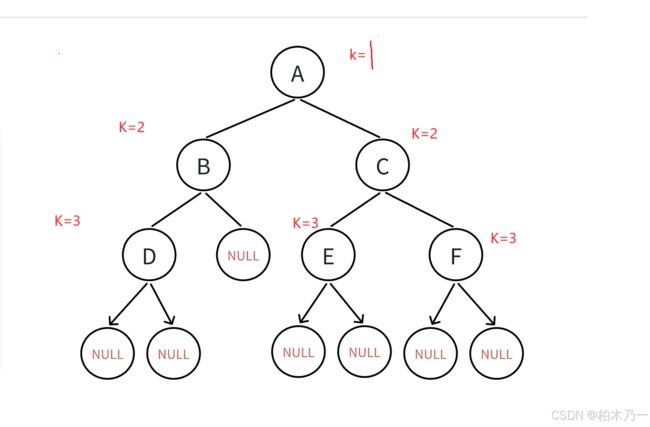
第k层的结点个数

我门用k-1方式去进行递归，去控制k层数，只进行传值操作。
函数声明为

int binarytreelevelKsize(BinraryTreeNode* root, int k);

在这里具体演示

因为每次进行的都是传值操作，所以每次函数栈帧销毁的时候，并不会影响上一层k的数字，例如在第三层销毁之后，第二层不会因此改变，这里不用传地址的妙处就在这里。
这里仍然有两个结束条件
如果结点为空，结束返回0
如果k==我想要的层数，返回1
这里提供具体代码

int binarytreelevelKsize(BinraryTreeNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}

	return binarytreelevelKsize(root->left, k-1) + binarytreelevelKsize(root->right, k-1);

}

如果该二叉树中只要第一层的结点，会在第二个if条件直接返回
如果没有的话，会进行下面的递归操作
此时总的第k层结点=左子树第k层的结点+右子树第k层的结点。

二叉树查找值为k的结点

该方法依旧采用递归的方式，先序遍历，它于上一个方法类似。它是在该结点所保存的数据如果和k相等，我们就返回。
所以函数声明是这样的

BinraryTreeNode* binarytreefind(BinraryTreeNode* root, BTdatatype k)

在这里仍然是两个结束条件
1.如果该结点为空，返回null
如果该结点保存的数据为和k相等的值的时候，我们返回该结点
如果根结点的值和k相等，会直接返回。
如果不是
会分别递归左右子树，把结果保存到两个二叉树结点类型的变量里
如果其中一个是真的就返回该结点
如果两个全是真的，返回第一个。如果两个全为假返回null。
代码如下

BinraryTreeNode* binarytreefind(BinraryTreeNode* root, BTdatatype k)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == k)
	{
		return root;
	}
	BinraryTreeNode* nodeleft = binarytreefind(root->left, k);
	
	if (nodeleft)
	{
		return nodeleft;
	}
	BinraryTreeNode* noderight = binarytreefind(root->right, k);
	if (noderight)
	{
		return noderight;
	}
	return NULL;
}

二叉树的深度

该方法与遍历二叉树的结点个数的方法类似，所以仍然采用递归的方法，前序遍历的方法，有所差异的是，它会分别遍历左右子树的深度并返回其中的较大值（每次递归都会进行）。

int binarytreedepth(BinraryTreeNode* root)

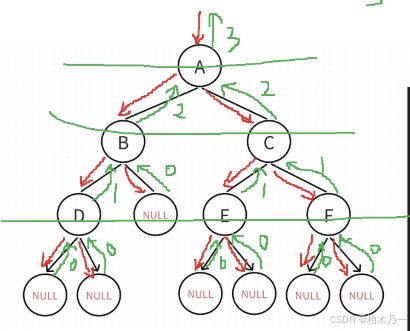
所以该函数只有一个结束条件就是它的结点为空，就返回0
返回结果是总深度=根节点＋左右子树的较大值
代码如下

int binarytreedepth(BinraryTreeNode* root)
{
	if (root == NULL)
	{
		return 0;

	}
	int rootleftdep = binarytreedepth(root->left);
	int rootrightdep = binarytreedepth(root->right);
	return 1 + (rootleftdep > rootrightdep ? rootleftdep : rootrightdep);

二叉树的销毁

二叉树的销毁采用后续遍历的方法，因为采用前序遍历的话，我们没法保证左右子树完全销毁，造成内存泄漏的问题，因为在先序遍历和中序遍历中，根结点总是在右子树之前遍历，最坏的结果就是整个左右子树完全内存泄漏，或右子树内存泄漏，所以采用后序遍历的方法，其他的与后续遍历的方法相似
代码如下

void binarytreedestory(BinraryTreeNode** root)
{
	if (*root == NULL)
	{
		return;
	}
	binarytreedestory(&((*root)->left));
	binarytreedestory(&((*root)->right));

	free(*root);
	*root = NULL;

}