《数据结构与算法分析:C语言描述_原书第二版》CH2算法分析_课后习题_部分解答
对于一个初学者来说,作者的Solutions Manual把太多的细节留给了读者,这里尽自己的努力给出部分习题的详解:
不当之处,欢迎指正。
1、 按增长率排列下列函数:N,√2,N1.5,N2,NlogN, NloglogN,Nlog2N,Nlog(N2),2/N,2N,2N/2,37,N2logN,N3。指出哪些函数以相同的增长率增长。
答:排列如下2/N < 37 < √2 < N < NloglogN < NlogN < Nlog(N2) < Nlog2N < N1.5 < N2 < N2logN < N3 < 2N/2 < 2N。
其中,NlogN 与 Nlog(N2) 的增长率相同,均为O(NlogN)。
补充说明:a) 其中 Nlog2N 与 N1.5, N3 与 2N/2大小关系的判定,可以连续使用洛必达法则(N->∞时,两个函数比值的极限,等于它们分别求导后比值的极限)。当然,更简单的是两边直接求平方。
b) 同时注意一个常用法则:对任意常数k,logkN = O(N)。这表明对数增长得非常缓慢。习题3中我们会证明它的一个更严格的形式。
2、 函数NlogN 与 N1+ε/√logN (ε>0) 哪个增长得更快?
分析:我们首先考虑的可能是利用洛必达法则,但是对于第二个函数其上下两部分皆含有变量,难以求导(当然也不是不行,就是麻烦些,如果你愿意设y = N1+ε/√logN ,然后对两边取对数的话)。这里我们将利用反证法:
要证NlogN < N1+ε/√logN ,即证 logN < Nε/√logN。既然用反证法,那么我们假设 Nε/√logN < logN。两边取对数有 ε/√logN logN < loglogN。即 ε√logN < loglogN。设t = logN,则 ε√t < logt <=> ε2t < log2t,这显然与连续1中b)矛盾,因此假设 Nε/√logN < logN 不成立。因此函数 N1+ε/√logN增长得更快。
3、 证明对任意常数k,logkN = o(N)。
解:要证明命题成立,只需证limn->∞(logkN / N) = 0即可。证明如下:
首先,如果k1 < k2,显然有 logk1N = o(logk2N) 。且k = 0时,logkn = 1。应用洛必达法则,limn->∞(logiN / N) = limn->∞(ilogi-1N / Nln2) = limn->∞(logi-1N / N) 。(说明:这里舍弃常数是因为我们假设函数最终的比值为0,否则不可简单的丢弃常数。当然如果比值不为零的话,我们需要返回到这里另行处理,其实证明过程也是不断尝试、调整的,此路不通,另行它法嘛:)就是说,通过不断地规约,最终极限的比值等于零,命题得证。
4、 求两个函数 f(N) 和 g(N),使得 f(N) ≠ O(g(N)) 且 g(N) ≠ O(f(N))。
一个显然的例子是函数 f(N) = sinN,g(N) = cosN。
5、 假设需要生成前N个自然数的一个随机置换。例如,{4,3,1,5,2} 和 {3,1,4,2,5} 就是合法的置换,但 {5,4,1,2,1} 却不是,因为数1出现两次而数3却没有出现。这个程序常常用于模拟一些算法。我们假设存在一个随机数生成器 RandInt(i, j),它以相同的概率生成 i 和 j 之间的一个整数。下面是三个算法:
1) 如下填入从 A[0] 到 A[N-1] 的数组 A:为了填入 A[i],生成随机数直到它不同于已经生成的 A[0],A[1],... ,A[i-1],再将其填入 A[i]。
2) 同算法1),但是要保存一个附加的数组,称之为 Used(用过的)数组。当一个随机数 Ran 最初被放入数组 A 的时候,置 Used[Ran] = 1。这就是说,当用一个随机数填入 A[i] 时,可以用一步来测试是否该随机数已经被使用,而不是像的一个算法那样(可能)进行 i 步测试。
3) 填写该数组使得 A[i] = i + 1。然后:
for(i = 1; i < N; i++) Swap(&A[i], &A[RandInt(0, i)]);
对每一个算法给出你能够得到的尽可能准确的期望的运行时间分析(用大O)。
解:分析,对于1),容易写出如下算法:
for(i = 0; i < N; i++){
while(1){
A[i] = RandInt(1, N);
for(j = 0; j < i; j++)
if(A[j] == A[i])
break;
if(j == i)
break;
}
}
调用一次随机数字生成函数与前面已经生成的随机数(存放在A数组中的)不同的概率为 (N-i) / N,那么理论上经过 N / (N-i) 次随机数的生成我们可以确定其与已生成的概率为 1。因此该算法的期望运行时间为
 ,
, 。
。
当然,也可以对分子放大的同时对分母缩小,不过这样求得的时间界限为O(N2),显然不如上面的做法精确。这里需要注意的一点是调和级数的前N项和,它是发散的,在计算机科学中的使用频率要远比在在数学等其它科目中使用得多。下面给出调和和: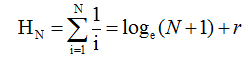
其近似误差r = 0.5772156649,这个值称为欧拉常数(Euler’s constant)。
对于2),容易写出如下算法:
for(i = 0; i < N; i++){
while(1){
A[i] = RandInt(1, N);
if(Used[i] == 0){
Used[i] = 1;
break;
}
}
}
同1)的分析,其运行时间界限显然为O(NlogN)。
对于3),运行时间为O(N),不消多说。
6、 记录一个称为Horner法则的算法,该算法用于计算 F(X) = Σi=0~nAiXi的值。
Poly = 0;
for(i = N; i >= 0; i--)
Poly = X * Ploy + A[i];
7、 给出一个有效的算法来确定在整数 A1 < A2 < A3 < ... < AN 的数组中是否存在整数 i ,使得 Ai = i。你的算法的运行时间是多少?
分析:类似二分查找,直接上代码:
int(int[] a, int N){
int low = 0, high = N - 1, middle;
while(low <= high){
middle = ((high-low) >> 1) + low;
if(a[middle]) < middle + 1)
low = middle + 1; // 搜索右空间
else if(a[middle] > middle + 1)
high = middle - 1; // 搜索左空间
else
return middle;
}
return -1;
}
易知该算法的运行时间为O(logN)。
8、 如果7题中的语句 low = middle + 1 更该为 low = middle ,那么这个程序还能正确运行吗?
答:不能,设 low = n,high = n + 1,则 middle = n,程序陷入死循环。
9、 a.编写一个程序来确定正整数N是否是素数,你的程序在最坏的情形下的运行时间是多少(用N表示)?(你应该能够写出O(√N)的算法程序)。
b.令B等于N的二进制表示法中的位数。B的值是多少?
c.你的程序在最坏情形下的运行时间是什么(用B表示)?
d.比较确定一个20(二进制)位的数是否是素数和确定一个40(二进制)位的数是否是素数的运行时间。
e.用 N 还是 B 来给出运行时间更合理,为什么?
解:对于a,由于 √N * √N = N,因此分解 N 时必有一个整数小于 √N。高效的算法思路是:首先,测试N是否能被2整除,不能的话测试N是否能被3,5,7,...,√N整除。编码如下(是素数返回1,不是返回0):
int IsPrime(int N){
int i;
if(N == 1)
return 0;
if(N % 2 == 0)
return 0;
for(i = 3; i <= int(sqrt(w) + 0.5); i += 2)
if(N % i == 0)
return 0;
return 1;
}
对于b,显然有,B = O(logN)。
对于c,由于B = O(logN),则2B = O(N),即2B/2 = O(√N),所以用B表示的最坏情况下的运行时间是:O(2B/2)
对于d,后者的运行时间是前者运行时间的平方,由c中的解答易知。
对于e,Wiss说:B is the better measure because it more accurately represents the size of the input.
All Rights Reserved.
Author:海峰:)
Copyright © xp_jiang.
转载请标明出处:http://www.cnblogs.com/xpjiang/p/4143743.html
参考资料:Data Structures and Algorithm Analysis in C(second edition) Solutions Manual_Mark Allen Weiss_Florida International University.