cuda编程入门——并行归约(五)

CUDA编程入门—并行归约（数组求和为例）

在并行计算中，归约（Reduction） 是一种将多个数据通过特定操作（如求和、求最大值等）合并为单一结果的并行算法。其核心目标是通过并行化加速大规模数据集的聚合计算。

关键概念

1. 操作类型：
   • 可结合且可交换的操作（如加法、乘法、最大值、最小值、逻辑与/或等）适合并行归约。
   • 若操作不可结合（如减法或除法），需特殊处理或无法直接并行化。
2. 并行实现方式：
   • 树形结构归约：将数据划分为多个块，每个线程/进程处理局部数据，逐步合并结果（如二叉树分层合并）。
   • 分块归约：将数据分块后局部归约，再全局归约（如MapReduce模型）。
   • 硬件加速：利用GPU的线程束（warp）或SIMD指令加速（如CUDA的shuffle指令）。

数组求和

相邻配对

例子：

__global__ void reduce(int *i_arr,int * o_arr, int size){

    unsigned int tid = threadIdx.x;
    int *idate = i_arr + blockIdx.x * blockDim.x; // 每个线程块的起始地址
    if(tid >= size){
        return;
    }
    /*
    1. 每个线程块内，相邻线程进行相加
    */
    for(int strid = 1; strid < blockDim.x; strid *= 2){
        __syncthreads();// 同步
        if(tid % (2 * strid) == 0){ 
            idate[tid] += idate[tid + strid];   // 相邻线程相加
        }
    }
    if(tid == 0){
        o_arr[blockIdx.x] = idate[0];// 每个线程块的结果写入输出数组    
    }

}

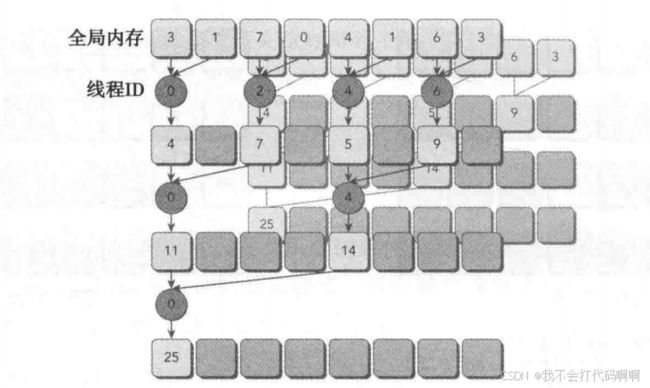
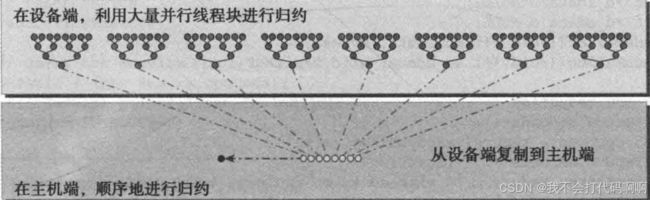
两个相邻元素间的距离被称为跨度，初始化均为1。在每一次归约循环结束后，这个间隔就被乘以2。在第一次循环结束后，idata(全局数据指针)的偶数元素将会被部分和替代。在第二次循环结束后，idata的每四个元素将会被新产生的部分和替代。因为线程块间无法同步，所以每个线程块产生的部分和被复制回了主机，并且在那儿进行串行求和，如下图

存在问题

在原代码的 if((tid%(2*stride)) == 0) 语句中，由于 tid （线程在块内的索引）对 2 * stride 取余的结果决定线程是否执行条件语句主体，在并行归约迭代过程中，会导致大量线程束分化。例如第一次迭代 stride = 1 时，仅偶数 tid 的线程执行，奇数 tid 的线程闲置但仍需被调度；随着迭代进行，如第二次迭代 stride = 2 时，只有四分之一的线程活跃，其余线程虽不执行核心计算但调度资源仍被占用，这极大浪费了 GPU 并行计算资源，降低了执行效率。

进行改进

__global__ void reduce2(int *i_arr, int *o_arr, int size) {
    unsigned int tid = threadIdx.x;
    unsigned int idx = blockIdx.x * blockDim.x + tid;
    int *idate = i_arr + blockIdx.x * blockDim.x; // 每个线程块的起始地址
    if (tid >= size) {
        printf("Thread %d out of bounds\n", tid);
        return;
    }
    /* b
    1. 每个线程块内，相邻线程进行相加
    */
    for (int strid = 1; strid < blockDim.x; strid *= 2) {
        int index = 2 * strid * tid;
        if (index < blockDim.x) {
            idate[tid] += idate[tid + strid];   // 相邻线程相加
        }
        __syncthreads(); // 同步
    }
}

• int index = 2 * stride * tid;：该语句通过将 2 、stride 与 tid 相乘来计算一个索引值 index 。这里，tid 是线程在其所在线程块内 x 维度的索引，stride 是归约操作中每次迭代的步长（从 1 开始，每次迭代翻倍）。这个计算方式是为了确定每个线程在当前归约迭代中要访问的数组元素在本地数组（由 idata 指向，对应线程块负责的数据段）中的位置。
• if (index < blockDim.x)：此条件判断用于检查计算得到的索引 index 是否在当前线程块的有效范围内（即小于线程块在 x 维度的大小 blockDim.x ）。若 index 在此范围内，线程将执行 idata[index] += idata[index + stride]; ，把 idata[index] 与 idata[index + stride] 的值相加，实现归约计算；若 index 超出范围，则不执行该加法操作，避免访问越界。

对于一个有512个线程的块来说，前8个线程束执行第一轮归约，剩下8个线程束什 么也不做。在第二轮里，前4个线程束执行归约，剩下12个线程束什么也不做。因此，这 样就彻底不存在分化了。在最后五轮中，当每一轮的线程总数小于线程束的大小时，线程总数小于线程束大小时，就无法填满整个线程束。此时，线程束内的线程在执行某些条件判断或操作时，由于数据特性或计算逻辑的不同，会导致部分线程执行特定指令，而另一些线程不执行，进而出现线程执行路径不一致，即线程束分化。

交错配对

_global__ void reduce3(int *i_arr, int *o_arr, int size) {
    unsigned int tid = threadIdx.x;
    unsigned int idx = blockIdx.x * blockDim.x + tid;
    int *idate = i_arr + blockIdx.x * blockDim.x; // 每个线程块的起始地址
    if (tid >= size) {
        printf("Thread %d out of bounds\n", tid);
        return;
    }
    for (int strid = blockDim.x/2; strid > 0; strid >>= 1) {
        if (tid < strid) {
            idate[tid] += idate[tid + strid];   // 交错线程相加
        }
        __syncthreads(); // 同步
    }
    if (tid == 0) {
        o_arr[blockIdx.x] = idate[0]; // 每个线程块的结果写入输出数组
    }
}

• 减少数据访问冲突
  • 在并行计算中，多个线程同时访问内存时可能会发生数据访问冲突，导致性能下降。采用交错配对的方式，每个线程访问的内存地址之间的间隔较大，相比于连续访问，减少了不同线程同时访问同一内存地址或同一缓存行的可能性。例如，当strid = blockDim.x/2时，一个线程访问idate[tid]，另一个线程访问idate[tid + strid]，它们访问的内存地址间隔较大，降低了内存访问冲突的概率，提高了内存访问效率。
• 提高并行度
  • 交错配对允许更多的线程同时进行计算，充分利用了 GPU 的并行计算能力。在每次迭代中，只要tid < strid，线程就可以进行计算，而不是像一些其他方法可能会限制只有部分特定线程才能进行计算。例如，在第一轮迭代中，一半的线程可以同时进行加法操作，下一轮迭代中，四分之一的线程可以同时进行操作，以此类推。这样可以在每一轮中充分利用可用的线程资源，提高了并行计算的效率，加快了计算速度。
• 利用局部性原理
  • 局部性原理包括时间局部性和空间局部性。在交错配对的过程中，线程访问的数据具有一定的空间局部性。因为线程访问的idate[tid]和idate[tid + strid]在内存中是相对靠近的，当一个线程访问了某个内存地址后，该地址附近的数据很可能已经被加载到缓存中，后续对相邻地址的访问可以直接从缓存中获取数据，大大提高了数据访问速度。例如，当strid较小时，相邻线程访问的数据在内存中是相邻的，利用了缓存的空间局部性，减少了从主存中读取数据的时间。
• 降低线程间的依赖程度
  • 在一些并行计算中，线程之间可能存在很强的依赖关系，导致线程必须按照特定的顺序执行，这会限制并行度和性能。而交错配对的方式使得线程之间的依赖关系相对较弱，每个线程只需要关注自己需要处理的数据和计算任务，不需要等待其他线程完成特定的操作后才能进行下一步。这样可以减少线程之间的等待时间，提高整体的计算性能。

展开规约

__global__ void reduce4(int *i_arr, int *o_arr, int size) {
    unsigned int tid = threadIdx.x;
    unsigned int idx = blockIdx.x * blockDim.x * 2 + tid;
    int *idate = i_arr + blockIdx.x * blockDim.x * 2; // 每个线程块的起始地址

    if(idx + blockDim.x < size) {
        idate[tid] += idate[tid + blockDim.x];   // 相邻线程相加
    }
    __syncthreads(); // 同步
    if (tid >= size) {
        printf("Thread %d out of bounds\n", tid);
        return;
    }
    for (int strid = blockDim.x/2; strid > 0; strid >>= 1) {
        if (tid < strid) {
            idate[tid] += idate[tid + strid];   // 交错线程相加
        }
        __syncthreads(); // 同步
    }
    if (tid == 0) {
        o_arr[blockIdx.x] = idate[0]; // 每个线程块的结果写入输出数组
}

增加并行粒度

• 扩大线程块数据处理量：通过将每个线程块对应的数据量乘以 2 （如 unsigned int idx = blockIdx.x * blockDim.x * 2 + threadIdx.x; 和 int *idata = g_idata + blockIdx.x * blockDim.x * 2; ），使每个线程块能处理更多数据。这减少了线程块的数量需求，降低了线程块调度等开销。在 GPU 中，线程块的调度和管理有一定成本，减少线程块数量可将更多资源用于实际计算，同时也能让每个线程块内的线程有更丰富的数据处理任务，提高整体并行计算的粒度和效率。
• 并行处理多段数据：在 if (idx + blockDim.x < n) g_idata[idx] += g_idata[idx + blockDim.x]; 操作中，利用扩大后的数据范围，让线程同时对两段不同的数据块进行初步合并。这相当于在全局内存层面并行执行了更多计算操作，增加了并行计算的并行度，能更快地处理数据，减少计算总时间。

优化内存访问

• 改善内存访问模式：改变后的内存访问模式（因数据量翻倍）更有利于硬件进行内存访问合并优化。GPU 的内存访问通常希望能以合并的方式进行，以提高内存带宽利用率。新的内存访问模式下，线程访问内存的地址偏移规律改变，使得在硬件层面更容易将多个线程的内存访问合并为一个或少数几个内存事务，减少内存访问冲突，提升内存访问效率。
• 减少内存访问次数：在全局内存中提前进行数据合并（上述两段数据块相加操作），减少了后续在本地内存（idata 指向的区域）中归约计算时的数据量。这意味着在后续的归约循环 for (int stride = blockDim.x / 2; stride > 0; stride >>= 1) 中，线程对本地内存的访问次数可能会减少，进一步降低内存访问开销，提高计算性能。

降低计算复杂度

• 简化归约计算流程：通过在全局内存中提前进行数据合并，降低了后续在本地内存中进行归约计算的复杂度。原本可能需要更多轮次或更复杂计算才能完成的归约任务，在经过全局内存初步合并后，变得相对简单。例如，后续在本地内存中的归约循环，由于数据量已经过初步合并减少，在相同的归约步长下，能更快地得到线程块内的归约结果，减少了计算的总轮次和计算量。
• 合理利用线程资源：在改进后的计算逻辑中，每个线程在不同阶段都有明确且更高效的任务。从全局内存的数据初步合并到本地内存的归约计算，线程资源得到了更充分的利用，避免了线程闲置或做低效计算的情况，提高了 GPU 计算资源的利用率，进而提升整体计算性能。

进阶

此代码为一次性处理两个线程块，可以扩展到处理8个，同时因为在线程数量小于线程束时会产生分化，在tid<32时进行优化判别

__global__ void reduce5(int *i_arr, int *o_arr, int size) {
    unsigned int tid = threadIdx.x;
    unsigned int idx = blockIdx.x * blockDim.x * 8 + tid;
    int *idate = i_arr + blockIdx.x * blockDim.x * 8; // 每个线程块的起始地址
    if(idx + 7*blockDim.x < size) {
        int a1 = idate[tid];
        int a2 = idate[tid + blockDim.x];
        int a3 = idate[tid + blockDim.x * 2];
        int a4 = idate[tid + blockDim.x * 3];
        int a5 = idate[tid + blockDim.x * 4];
        int a6 = idate[tid + blockDim.x * 5];
        int a7 = idate[tid + blockDim.x * 6];
        int a8 = idate[tid + blockDim.x * 7];
        idate[tid] = a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8;   // 相邻线程相加
    }
    __syncthreads(); // 同步
    if (tid >= size) {
        printf("Thread %d out of bounds\n", tid);
        return;
    }
    if(blockDim.x >= 1024 && tid < 512) {
        idate[tid] += idate[tid + 512];   // 相邻线程相加
    }
    __syncthreads(); // 同步
    if(blockDim.x >= 512 && tid < 256) {
        idate[tid] += idate[tid + 256];   // 相邻线程相加
    }
    __syncthreads(); // 同步
    if(blockDim.x >= 256 && tid < 128) {
        idate[tid] += idate[tid + 128];   // 相邻线程相加
    }
    __syncthreads(); // 同步
    if(blockDim.x >= 128 && tid < 64) {
        idate[tid] += idate[tid + 64];   // 相邻线程相加
    }
    __syncthreads(); // 同步
    
    if(tid < 32)
    {
        volatile int *idata = (volatile int *)i_arr;
        idata[tid] += idata[tid + 32];   // 相邻线程相加
        idate[tid] += idate[tid + 16];   // 相邻线程相加
        idate[tid] += idate[tid + 8];   // 相邻线程相加
        idate[tid] += idate[tid + 4];   // 相邻线程相加
        idate[tid] += idate[tid + 2];   // 相邻线程相加
        idate[tid] += idate[tid + 1];   // 相邻线程相加

    }
   
    if (tid == 0) {
        o_arr[blockIdx.x] = idate[0]; // 每个线程块的结果写入输出数组

}