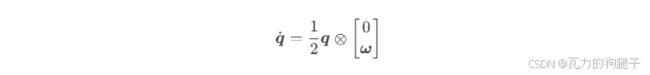Starlink卫星动力学系统仿真建模第十讲-基于SMC和四元数的卫星姿态控制示例及Python实现
基于四元数与滑模控制的卫星姿态控制
一、基本原理
1. 四元数姿态表示
四元数运动学方程：
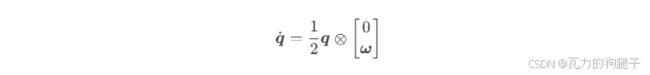
3. 滑模控制设计
二、代码实现（Python）
1. 四元数运算工具
import numpy as np
def quat_mult(q1, q2):
"""四元数乘法"""
w1, x1, y1, z1 = q1
w2, x2, y2, z2 = q2
w = w1*w2 - x1*x2 - y1*y2 - z1*z2
x = w1*x2 + x1*w2 + y1*z2 - z1*y2
y = w1*y2 - x1*z2 + y1*w2 + z1*x2
z = w1*z2 + x1*y2 - y1*x2 + z1*w2
return np.array([w, x, y, z])
def quat_conj(q):
"""四元数共轭"""
return np.array([q[0], -q[1], -q[2], -q[3]])
def quat_error(q_current, q_desired):
"""计算误差四元数 q_e = q_desired ⊗ q_current^{-1}"""
q_conj = quat_conj(q_current)
return quat_mult(q_desired, q_conj)
2. 滑模控制器
class QuaternionSMC:
def __init__(self, J, lambda_, K, dt):
self.J = J # 转动惯量矩阵 (3x3)
self.lambda_ = lambda_
self.K = K # 切换增益
self.dt = dt
def compute_control(self, q, omega, q_d, omega_d):
# 计算误差四元数
q_e = quat_error(q, q_d)
q_e_v = q_e[1:] # 提取向量部分 [q1, q2, q3]
# 角速度误差
omega_e = omega - omega_d
# 滑模面 s = omega_e + lambda * q_e_v
s = omega_e + self.lambda_ * q_e_v
# 等效控制 u_eq = J*(d(omega_d)/dt - lambda*0.5*omega × q_e_v) + omega × J omega
# 假设目标角加速度为0（omega_d为常数）
u_eq = np.dot(self.J, -self.lambda_ * 0.5 * np.cross(omega, q_e_v)) \
+ np.cross(omega, np.dot(self.J, omega))
# 切换控制 u_sw = -K * sign(s)
u_sw = -self.K * np.sign(s)
# 总控制力矩
u = u_eq + u_sw
return u
3. 卫星姿态动力学仿真
def simulate_satellite_attitude():
# 参数初始化
J = np.diag([100, 100, 80]) # 转动惯量 (kg·m²)
lambda_ = 0.5
K = 20.0
dt = 0.01
# 初始状态
q = np.array([1.0, 0.0, 0.0, 0.0]) # 初始姿态（无旋转）
omega = np.array([0.0, 0.0, 0.0]) # 初始角速度
q_d = np.array([0.707, 0.0, 0.707, 0.0]) # 目标姿态（绕x轴旋转90度）
omega_d = np.array([0.0, 0.0, 0.0]) # 目标角速度
controller = QuaternionSMC(J, lambda_, K, dt)
# 记录数据
time = np.arange(0, 10, dt)
q_history = []
omega_history = []
for t in time:
# 计算控制力矩
u = controller.compute_control(q, omega, q_d, omega_d)
# 加入扰动（模拟太阳辐射压力）
disturbance = np.array([0.1*np.sin(t), 0.1*np.cos(t), 0.05*np.sin(2*t)])
u += disturbance
# 更新角速度（欧拉积分）
omega_dot = np.linalg.inv(J).dot(-np.cross(omega, J.dot(omega)) + u/J.diagonal()
omega = omega + omega_dot * dt
# 更新四元数（四阶龙格-库塔法）
k1 = 0.5 * quat_mult(q, np.array([0, omega[0], omega[1], omega[2]]))
k2 = 0.5 * quat_mult(q + 0.5*dt*k1, np.array([0, omega[0], omega[1], omega[2]]))
k3 = 0.5 * quat_mult(q + 0.5*dt*k2, np.array([0, omega[0], omega[1], omega[2]]))
k4 = 0.5 * quat_mult(q + dt*k3, np.array([0, omega[0], omega[1], omega[2]]))
q = q + (dt/6)*(k1 + 2*k2 + 2*k3 + k4)
q /= np.linalg.norm(q) # 归一化
# 记录数据
q_history.append(q)
omega_history.append(omega)
return time, np.array(q_history), np.array(omega_history)
三、使用示例
可视化代码
import matplotlib.pyplot as plt
time, q_history, omega_history = simulate_satellite_attitude()
# 绘制四元数误差
plt.figure()
plt.plot(time, q_history[:, 0], label='q0')
plt.plot(time, q_history[:, 1], label='q1')
plt.plot(time, q_history[:, 2], label='q2')
plt.plot(time, q_history[:, 3], label='q3')
plt.xlabel('Time (s)')
plt.ylabel('Quaternion')
plt.legend()
plt.title('Attitude Quaternion')
# 绘制角速度
plt.figure()
plt.plot(time, omega_history[:, 0], label='ω_x')
plt.plot(time, omega_history[:, 1], label='ω_y')
plt.plot(time, omega_history[:, 2], label='ω_z')
plt.xlabel('Time (s)')
plt.ylabel('Angular Velocity (rad/s)')
plt.legend()
plt.title('Angular Velocity')
plt.show()
四、改进与注意事项
- 自适应增益：
- 根据扰动估计动态调整 ( K )，降低保守性。
- 执行器饱和：
- 在控制律中增加力矩限幅，避免超出执行器能力。
五、总结
- 优势：
- 四元数避免奇异性，滑模控制提供强鲁棒性，适合存在扰动和模型不确定性的卫星姿态控制。
- 挑战：
- 抖振可能影响执行器寿命，需结合高阶滑模或滤波技术。
- 应用扩展：
- 可结合姿态确定系统（如星敏感器、陀螺仪）实现闭环控制。