树状数组(二叉索引树)
树状数组(二叉索引树)
-
树状数组的核心思想:分治。将数组以二叉树的逻辑结构进行组织。树状数组巧妙的利用了下标的二进制特性,以维护区间信息。
树状数组并非一棵真正的二叉树,以二叉树的存储结构进行组织的为线段树。
-
lowbit \texttt{lowbit} lowbit操作:获取整数最低位的1的位置。由于0的 lowbit \texttt{lowbit} lowbit没有意义,因此树状数组下标需从1开始。
int lowbit(int i){
return i&(-i);
}
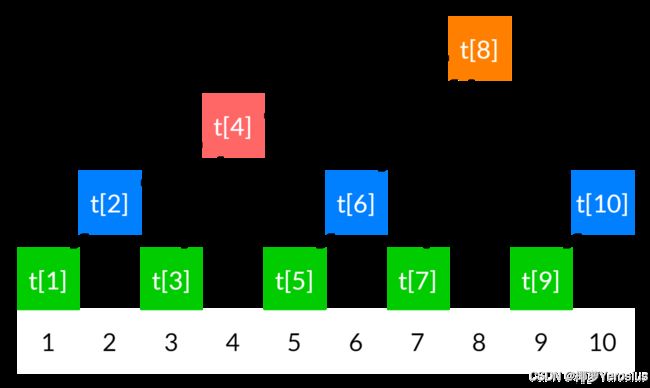
- 设序列 a a a的长度为 n n n,树状数组为 t t t并与其等长。对于每个元素 a i a_i ai,其具有管理区间 [ i − lowbit ( i ) + 1 , i ] [i-\texttt{lowbit}(i)+1,i] [i−lowbit(i)+1,i],用于管理其区间信息。如区间之和、可重复贡献性问题(区间最值、区间 GCD \texttt{GCD} GCD)等。
t 1 = o p t ( a 1 ) ; t 2 = o p t ( t 1 , a 2 ) ; t 3 = o p t ( a 3 ) ; t 4 = o p t ( t 2 , t 3 , a 4 ) ; t 5 = o p t ( a 5 ) ; t 6 = o p t ( t 5 , a 6 ) ; t 7 = o p t ( a 7 ) ; t 8 = o p t ( t 4 , t 6 , t 7 , a 8 ) ; … t_1=opt(a_1);\\t_2=opt(t_1,a_2);\\t_3=opt(a_3);\\t_4=opt(t_2,t_3,a_4);\\t_5=opt(a_5);\\t_6=opt(t_5,a_6);\\t_7=opt(a_7);\\t_8=opt(t_4,t_6,t_7,a_8);\\\dots t1=opt(a1);t2=opt(t1,a2);t3=opt(a3);t4=opt(t2,t3,a4);t5=opt(a5);t6=opt(t5,a6);t7=opt(a7);t8=opt(t4,t6,t7,a8);…
区间和
单点修改 区间查询(前缀和版树状数组)
void change(int i,int d);//单点修改
void init(){//初始化树状数组:对所有元素调用单点修改
for(int i=1;i<=n;i++)
change(i,a[i]);
}
- 单点修改(向上修改)
以 a [ x ] + = d a[x]+=d a[x]+=d为例:由于管理区间具有前缀性,因此需修改整个树状数组中所有位于 x x x之后且包含 x x x的管理区间。
void change(int x,int d){//以a[x]+=d为例
a[x]+=d;
for(;x<=n;x+=lowbit(i))//向上修改,跳跃到下一个包含x的管理区间,n为原数组长度
tree[x]+=d;
}
- 区间查询(向下查询)
以查询 [ l , r ] [l,r] [l,r]区间为例:由于管理区间具有前缀性,因此求解 [ l , r ] [l,r] [l,r],需分别求解 [ 1 , l ] , [ 1 , r ] [1,l],[1,r] [1,l],[1,r]再相减。对于每个查询端点,需用其之前的若干个管理区间,以拼接成 1 1 1到其的区间。
为什么不能直接从 l l l向上查询到 r r r?由于管理区间具有前缀性,直接计算会导致 [ 1 , l ] [1,l] [1,l]区间信息被重复计算,这对于非可重复贡献性问题是不可接受的(如区间之和、区间之积等)。
int l,r;
int query(int i){//向下查询
int ans=0;
for(;i;i-=lowbit(i))//跳跃到上一个管理区间
ans+=tree[i];
return ans;
}
//调用:query(r)-query(l-1);
区间修改 单点查询(差分版树状数组)
原理:差分是前缀和的逆运算。仅需将树状数组存储内容修改为差分数组,即可实现区间修改操作。
- 区间修改
void modify(int l,int r,int d){//[l,r]均+d
update(l,d),update(r+1,-d);
}
//初始化树状数组:传入差分数组
for(int i=1;i<=n;i++) update(i,a[i]-a[i-1]);
- 单点查询:差分数组求前缀和即为原数组,因此调用
query函数即可
区间修改+区间查询(二阶树状数组)
标准解法为线段树。
-
区间修改原理:前缀和与差分互为逆运算, a k = ∑ i = 1 k d i a_k=\sum\limits_{i=1}^{k}d_i ak=i=1∑kdi
-
区间查询: ∑ i = L R a i = ∑ i = 1 R a i − ∑ i = 1 L − 1 a i \sum\limits_{i=L}^{R} a_i=\sum\limits_{i=1}^{R}a_i-\sum\limits_{i=1}^{L-1}a_i i=L∑Rai=i=1∑Rai−i=1∑L−1ai,因此转换为 ∑ i = 1 k a i ( k ∈ { L − 1 , R } ) \sum\limits_{i=1}^{k}a_i(k\in \set{L-1,R}) i=1∑kai(k∈{L−1,R})问题
考查 ∑ i = 1 k a i \sum\limits_{i=1}^{k}a_i i=1∑kai: a 1 + a 2 + ⋯ + a k = d 1 + ( d 1 + d 2 ) + ⋯ + ( d 1 + ⋯ + d k ) = k × d 1 + ( k − 1 ) × d 2 + ⋯ + d k a_1+a_2+\dots+a_k=d_1+(d_1+d_2)+\dots+(d_1+\dots+d_k)=k\times d_1+(k-1)\times d_2+\dots+d_k a1+a2+⋯+ak=d1+(d1+d2)+⋯+(d1+⋯+dk)=k×d1+(k−1)×d2+⋯+dk
= k ∑ i = 1 k d i − ∑ i = 1 k ( i − 1 ) d i =k\sum\limits_{i=1}^{k} d_i-\sum\limits_{i=1}^{k}(i-1)d_i =ki=1∑kdi−i=1∑k(i−1)di
因此,维护两个树状数组,分别用于实现 d i d_i di与 ( i − 1 ) d i (i-1)d_i (i−1)di
void update1(int i,int d){
for(;i<=n;i+=lowbit(i))
t1[i]+=d;
}
void update2(int i,int num){
for(;i<=n;i+=lowbit(i))
t2[i]+=num;
}
int query1(int i){
int ans=0;
for(;i;i-=lowbit(i))
ans+=t1[i];
return ans;
}
int query2(int i){
int ans=0;
for(;i;i-=lowbit(i))
ans+=t2[i];
return ans;
}
void init(){
for(int i=1;i<=n;i++){
update1(i,a[i]-a[i-1]);
update2(i,(i-1)*(a[i]-a[i-1]));
}
}
- 区间修改
void modify(int l,int r,int d){
update1(l,d),update1(r+1,-d);
update2(l,(l-1)*d),update2(r+1,(r+1-1)*(-d));
}
- 区间查询
int query(int l,int r){
return (r*query1(r)-query2(r))-((l-1)*query1(l-1)-query2(l-1));
}
区间最值( O ( n × ( log 2 n ) 2 + q × ( log 2 n ) 2 ) \mathcal{O}(n\times (\log_2{n})^2+q\times (\log_2{n})^2) O(n×(log2n)2+q×(log2n)2))
修改树状数组为存储其管理区间内的最值。
单点修改:需将 n n n个数初始化到树状数组中,共有 log 2 n \log_2{n} log2n步更新。
区间查询:
- 若 R − L ≥ lowbit ( R ) R-L\ge \texttt{lowbit}(R) R−L≥lowbit(R),则 R R R管理区间 ⊆ [ L , R ] \subseteq [L,R] ⊆[L,R],继续向前递推即可。 max/min [ L , R ] = max/min ( max/min [ R − lowbit ( R ) + 1 , R ] , max/min [ L , R − lowbit ( R ) ] ) \texttt{max/min}[L,R]=\texttt{max/min}(\texttt{max/min}[R-\texttt{lowbit}(R)+1,R],\texttt{max/min}[L,R-\texttt{lowbit}(R)]) max/min[L,R]=max/min(max/min[R−lowbit(R)+1,R],max/min[L,R−lowbit(R)]);
- 若 R − L < lowbit ( R ) R-L<\texttt{lowbit}(R) R−L<lowbit(R),则 [ L , R ] ⊆ R [L,R]\subseteq R [L,R]⊆R的管理区间, ∃ \exists ∃元素 ∉ [ L , R ] \notin[L,R] ∈/[L,R]。应使用原数组的 a [ R ] a[R] a[R],再向前递推到 R − 1 R-1 R−1的管理区间。 max/min [ L , R ] = max/min ( a [ R ] , max/min [ L , R − 1 ] ) \texttt{max/min}[L,R]=\texttt{max/min}(a[R],\texttt{max/min}[L,R-1]) max/min[L,R]=max/min(a[R],max/min[L,R−1])。
求逆序数( O ( n log 2 n ) O(n\log_2n) O(nlog2n))
核心思想:将原数组元素视为树状数组的下标。每处理一个元素 x x x,树状数组 t r e e [ x ] tree[x] tree[x]++。
for(int i=1;i<=n;i++){//正序处理
change(a[i],1);
ans+=i-query(a[i]);
}
for(int i=n;i;i--){//逆序处理
change(a[i],1);
ans+=query(a[i]-1);
}