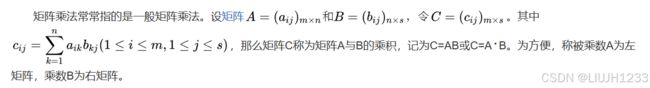探讨矩阵：从基础到应用

一. 矩阵的定义

由 n×m 个数aij排成的n行m列的数表称为n行m列的矩阵，简称n×m矩阵。记作：

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

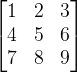
二. 矩阵的基本运算

2.1 矩阵加法

        ​​​​​​​        ​​​​​​​                ​​​​​​​

矩阵加法一般是指两个矩阵把其相对应元素加在一起的运算。(一般来说，两个矩阵行列相等，包括减法也是)

2.2 矩阵减法

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

矩阵减法与加法类似，也是对两个同型矩阵对应位置的元素相减。

2.3 矩阵乘法

若有一个x行y列的矩阵与一个y行z列的矩阵，他们就可以相乘，得到一个x行z列的矩阵。

但是，相乘方式与加减法不同。

2.4 代码模板

现在，我们就可以根据上面的定义写一个自己的代码模板。

这是代码模板：

struct Mat {//构造结构体来进行矩阵计算，储存
    int a[105][105];
    int r, c;

    Mat(int _r = 0, int _c = 0) {
        r = _r, c = _c;
        memset(a, 0, sizeof a);
        if (c == 0)
            c = r;
    }//构造函数，如果是方阵，只给了行，那就把行的值赋给列

    Mat operator+(const Mat& q) const {//通过运算符重载，把 “+” 变为 “矩阵+”
        Mat ans = *this;		
        for (int i = 1; i <= r; i++) {
            for (int j = 1; j <= c; j++) {
                ans.a[i][j] += q.a[i][j];
            }
        }
        return ans;
    }//矩阵加法

    Mat operator-(const Mat& q) const {
        Mat ans = *this;
        for (int i = 1; i <= r; i++) {
            for (int j = 1; j <= c; j++) {
                ans.a[i][j] -= q.a[i][j];
            }
        }
        return ans;
    }//矩阵减法

    Mat operator*(const Mat& q) const {
        Mat ans(r, q.c);
        int n = r, m = q.c;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                for (int k = 1; k <= c; k++)
                    ans.a[i][j] += a[i][k] * q.a[k][j];
        return ans;
    }//矩阵乘法

};

三. 单位元

3.1 单位元的定义

单位元是集合中的一个特殊元素，它在与其他元素的运算过程中保持不变性。具体来说：

当单位元与自身相乘时，得到的结果等于原单位元本身。

如果单位元与另一个元素相乘，得到的也是这个元素本身。

根据单位元的定义，我们就可以求单位矩阵了

3.2 单位矩阵

一个4*4的单位矩阵，是这样的：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

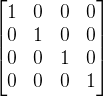
我们发现这个矩阵是主对角线为1，其他为0的一个矩阵。

3.3 单位矩阵代码

    void unit() {
        // 单位函数
        memset(a, 0, sizeof a);
        for (int i = 1; i <= r; i++)
            a[i][i] = 1;
    }

四.总代码

struct Mat {
    int a[105][105];
    int r, c;
    Mat(int _r = 0, int _c = 0) {
        r = _r, c = _c;
        memset(a, 0, sizeof a);
        if (c == 0)
            c = r;
    }
    void unit() {
        // 单位函数
        memset(a, 0, sizeof a);
        for (int i = 1; i <= r; i++)
            a[i][i] = 1;
    }
    Mat operator+(const Mat& q) const {
        Mat ans = *this;		
        for (int i = 1; i <= r; i++) {
            for (int j = 1; j <= c; j++) {
                ans.a[i][j] += q.a[i][j];
            }
        }
        return ans;
    }
    Mat operator-(const Mat& q) const {
        Mat ans = *this;
        for (int i = 1; i <= r; i++) {
            for (int j = 1; j <= c; j++) {
                ans.a[i][j] -= q.a[i][j];
            }
        }
        return ans;
    }
    Mat operator*(const Mat& q) const {
        Mat ans(r, q.c);
        int n = r, m = q.c;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                for (int k = 1; k <= c; k++)
                    ans.a[i][j] += a[i][k] * q.a[k][j];
        return ans;
    }
    void input() {
        for (int i = 1; i <= r; i++)
            for (int j = 1; j <= c; j++)
                cin >> a[i][j];
    }
    void output() {
        for (int i = 1; i <= r; i++) {
            for (int j = 1; j <= c; j++) {
                cout << a[i][j] << " ";
            }
            cout << endl;
        }
    }
};

int main() {
    return 0;
}

五.矩阵加速

5.1 概念

线性递推式的矩阵表示：
很多线性递推式可以表示为矩阵的幂的形式。例如，斐波那契数列的第n项可以通过一个2x2的矩阵的n-1次幂来高效计算。这种表示方法使得我们可以利用矩阵乘法的性质来优化计算。

5.2 例题《斐波那契数列》

算法时间复杂度到O(n)，在大数据中略显吃力，所以我们要优化。

我们先写出递推式

我们写出矩阵:

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

现在，我们只需要求出 a,b,c,d 的值就行。

又因为：

所以 a=1,b=1,c=1,d=0;

得出;

        ​​​​​​​        ​​​​​​​        

就可以快速求出斐波那契数列

5.3 AC代码

#include
using namespace std;
const int N=105;
const int mod=1e9+7;
long long n;
struct Mat{
    int a[N][N],r,c;
    Mat(int _r=0,int _c=0){
        r=_r,c=_c;
        memset(a,0,sizeof a);
        if(c==0){
            c=r;
        }
    }
    void unit(){
        memset(a,0,sizeof a);
        for(int i=1;i<=r;++i){
            a[i][i]=1;
        }
    }
    Mat operator*(const Mat& t)const{
        Mat ans(r,t.c);
        for(int i=1;i<=r;++i){
            for(int j=1;j<=t.c;j++){
                for(int k=1;k<=c;++k){
                    ans.a[i][j]+=((long long)a[i][k]*t.a[k][j])%mod;
                    ans.a[i][j]%=mod;
                }
            }
        }
        return ans;
    }
    Mat qpow(long long n){
        Mat ans(r,c);
        ans.unit();
        Mat t=*this;
        while(n){
            if(n&1){
                ans=ans*t;
            }
            t=t*t;
            n>>=1;
        }
        return ans;
    }
}A(2,2);
int main(){
    scanf("%lld",&n);
    A.a[1][1]=0,A.a[1][2]=1,A.a[2][1]=1,A.a[2][2]=1;
    Mat t=A.qpow(n-1);
    cout<

加纳！！！！！