第七节:AVL树基本操作实现
一、AVL树基本原理
AVL树是一种自平衡二叉搜索树,通过平衡因子(bf)机制维护树的平衡性。其核心特性:
- 每个节点的平衡因子定义为:右子树高度 - 左子树高度
- 平衡因子绝对值不超过1(|bf| ≤ 1)
- 当插入/删除导致失衡(|bf| ≥ 2)时,通过旋转操作恢复平衡
- 通过四种旋转操作修正失衡:
| 旋转类型 | 触发条件 | 操作流程 |
|---|---|---|
LL |
左子树的左子树过高 (BF=-2→-1) | 单次右旋 |
RR |
右子树的右子树过高 (BF=+2→+1) | 单次左旋 |
LR |
左子树的右子树过高 (BF=-2→+1) | 先左旋子节点再右旋 |
RL |
右子树的左子树过高 (BF=+2→-1) | 先右旋子节点再左旋 |
平衡机制保证树的高度始终为O(log n),实现高效的查找、插入、删除操作。
二、AVL树实现思路与接口函数
2.1 AVL树结点的定义
template<class K, class V>
struct AVLTreeNode
{
pair<K, V> _kv; // 键值对
AVLTreeNode* _left; // 左子树
AVLTreeNode* _right; // 右子树
AVLTreeNode* _parent; // 父节点
int _bf; // 平衡因子
};
2.2 辅助函数
| 函数名 | 功能描述 |
|---|---|
RotateL |
左单旋 |
RotateR |
右单旋 |
RotateLR |
左右双旋 |
RotateRL |
右左双旋 |
IsBalance() |
验证树是否平衡 |
Height() |
计算子树高度 |
InorderPrint() |
遍历输出结点键值 |
2.3 操作函数
| 函数名 | 功能描述 |
|---|---|
Find() |
查找指定键的节点 |
UpDate() |
修改指定键节点的值 |
Insert() |
插入键值对 |
三、辅助函数设计
3.1 左单旋(LL型失衡)
说在前面:由于四大选旋转操作算法实现都差不多,这里我们详细分析左单旋,其他三个旋转会在最后以代码的形式呈现。
1.操作示意图
// 左单旋前(失衡状态)
A (bf=+2)
\
B (bf=1)
/ \
β C // 这里的β可能有,可能没有,假设没有
// 左单旋后(平衡状态)
B (bf=0)
/ \
A C
\
β
2.节点关系变化表
| 节点 | 旋转前关系 | 旋转后关系 | 平衡因子变化 |
|---|---|---|---|
| A | 根节点 | B的左子节点 | +2 → 0 |
| B | A的右子节点 | 根节点 | +1 → 0 |
| C | B的右子节点 | B的右子节点 | 保持 |
| β | B的左子节点 | A的右子节点 | 保持 |
3. 平衡因子重置逻辑
- 原失衡节点A的右子树高度降低1
- 新根节点B的左右子树高度差归零
- β子树从B的左子树变为A的右子树,不影响整体平衡因子计算
4. 函数设计分析
左单旋算法(RotateL)
├─ 1. 获取关键节点
│ ├─ subR = parent→right // B节点
│ └─ subRL = subR→left // β子树
│
├─ 2. 调整右指针链
│ ├─ parent→right = subRL // A的右指针指向β
│ └─ if (subRL) subRL→parent = parent
│
├─ 3. 建立新父子关系
│ ├─ subR→left = parent // B的左指针指向A
│ └─ parent→parent = subR // A的父指针指向B
│
├─ 4. 处理祖父节点连接
│ ├─ Case 1: 原父节点是根节点
│ │ ├─ _root = subR
│ │ └─ subR→parent = nullptr
│ │
│ └─ Case 2: 原父节点非根节点
│ ├─ if (ppNode→left == parent)
│ │ └─ ppNode→left = subR
│ └─ else
│ └─ ppNode→right = subR
│
├─ 5. 平衡因子重置
│ ├─ parent→bf = 0 // 原失衡节点
│ └─ subR→bf = 0 // 新父节点
│
└─ 6. 边界条件处理
├─ subRL为空时的处理
├─ 根节点更新验证
└─ 指针安全检测
5. 函数代码
void RotateL(Node* parent)
{
// 1.保存关键结点信息
Node* subR = parent->_right;
Node* subRL = subR->_left;
// 2.建立 parent 与 subRL 联系
parent->_right = subRL;
if (subRL) subRL->_parent = parent;
// 3.处理 parent 与 subR 的联系
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
// 4.重建 parent 与上层结点的关系
if (!ppNode) // parent 是根节点
{
_root = subR;
_root->_parent = nullptr;
}
else // parent 不是根节点
{
if (ppNode->_left == parent) ppNode->_left = subR;
else ppNode->_right = subR;
subR->_parent = ppNode;
}
// 5. 更新平衡因子
parent->_bf = subR->_bf = 0;
}
3.2 计算树的高度
1. 函数设计分析
计算树高度算法(Height)
├─ 1. 函数入口
│ └─ 参数: Node* root (当前子树根节点)
│
├─ 2. 递归终止条件
│ └─ if (root == nullptr)
│ └─ return 0; // 空树高度为0
│
├─ 3. 递归计算左子树高度
│ └─ int leftH = Height(root->_left)
│ ├─ 深入左子树递归
│ └─ 返回左子树高度值
│
├─ 4. 递归计算右子树高度
│ └─ int rightH = Height(root->_right)
│ ├─ 深入右子树递归
│ └─ 返回右子树高度值
│
├─ 5. 计算当前子树高度
│ └─ return max(leftH, rightH) + 1
│ ├─ 取左右子树较大高度
│ └─ +1 包含当前层高度
│
└─ 6. 递归展开过程示例
└─ 示例树:A(B(D), C(E,F))
├─ Height(A)
│ ├─ leftH = Height(B) = 2
│ │ ├─ Height(D) = 1
│ │ └─ max(1,0)+1=2
│ ├─ rightH = Height(C) = 2
│ │ ├─ Height(E)=1
│ │ └─ Height(F)=1
│ └─ max(2,2)+1=3
└─ 最终返回高度3
2. 函数代码
int Height(Node* root)
{
if (root == nullptr) return 0;
else return max(Height(root->_left), Height(root->_right)) + 1;
}
3.3 判断AVL树是否平衡
1. 函数设计分析
IsBalance算法
├─ 1. 递归终止条件
│ └─ if (root == nullptr)
│ └─ return true // 空树视为平衡
│
├─ 2. 计算子树高度
│ ├─ leftH = Height(root→_left) // 左子树高度
│ └─ rightH = Height(root→_right) // 右子树高度
│
├─ 3. 平衡因子验证
│ └─ if (rightH - leftH != root→_bf)
│ ├─ 输出错误节点信息
│ └─ return false
│
├─ 4. 当前节点平衡检查
│ └─ if (abs(rightH - leftH) >= 2)
│ └─ return false
│
├─ 5. 递归验证子树
│ ├─ 左子树检查:IsBalance(root→_left)
│ └─ 右子树检查:IsBalance(root→_right)
│
└─ 6. 返回最终结果
└─ return (步骤4结果 && 左子树结果 && 右子树结果)
执行路径示例:
root(A)
├─ 计算A的leftH/rightH
├─ 验证A.bf == rightH-leftH?
├─ 检查|rightH-leftH|<2
├─ 递归检查A.left(B)
│ ├─ 计算B的leftH/rightH
│ └─ ...(递归展开)
└─ 递归检查A.right(C)
├─ 计算C的leftH/rightH
└─ ...(递归展开)
2. 函数代码
bool IsBalance(Node* root)
{
if (root == nullptr) return true;
int leftH = Height(root->_left);
int rightH = Height(root->_right);
if (rightH - leftH != root->_bf)
{
cout << "平衡因子异常:" << root->_kv.first << endl;
return false;
}
return abs(rightH - leftH) < 2
&& IsBalance(root->_left)
&& IsBalance(root->_right);
}
3.4 中序遍历打印
1. 函数设计分析
中序遍历算法(InorderPrint)
├─ 1. 递归终止条件
│ └─ if (root == nullptr)
│ └─ return; // 空子树直接返回
│
├─ 2. 递归遍历左子树
│ └─ InorderPrint(root→_left)
│ ├─ 深入左子树递归
│ └─ 按"左-根-右"顺序保证有序性
│
├─ 3. 处理当前节点
│ └─ 输出格式:
│ "[键:值(bf=平衡因子)] "
│ ├─ 示例:[15:apple(bf=0)]
│ └─ 显示完整节点信息
│
├─ 4. 递归遍历右子树
│ └─ InorderPrint(root→_right)
│ ├─ 深入右子树递归
│ └─ 完成右子树遍历
│
└─ 5. 递归展开示例
└─ 树结构:A(20)
/ \
B(10) C(30)
遍历顺序:
1. B的递归左(空返回)
2. 输出B [10:...]
3. B的递归右(空返回)
4. 输出A [20:...]
5. C的递归左(空返回)
6. 输出C [30:...]
7. C的递归右(空返回)
最终输出序列:[B] → [A] → [C]
2. 函数代码
void InorderPrint(Node* root) const
{
if (root == nullptr) return;
// 1. 遍历左子树
InorderPrint(root->_left);
// 2. 访问当前节点
cout << "[" << root->_kv.first
<< ":" << root->_kv.second
<< "(bf=" << root->_bf << ")] ";
// 3. 遍历右子树
InorderPrint(root->_right);
}
四、AVL树的基本操作函数
4.1 查找结点
1. 函数设计分析
查找算法(Find)
├─ 1. 初始化当前节点
│ └─ cur = _root
├─ 2. 循环遍历
│ ├─ while (cur != nullptr)
│ │ ├─ 比较键值
│ │ │ ├─ cur.key < key → 右移
│ │ │ ├─ cur.key > key → 左移
│ │ │ └─ 相等 → 返回节点
│ │ └─ 更新cur指针
└─ 3. 未找到情况
└─ return nullptr
2. 函数代码
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < key) cur = cur->_right;
else if (cur->_kv.first > key) cur = cur->_left;
else return cur;
}
return nullptr;
}
4.2 修改节点
1. 函数设计分析
更新值算法(UpDate)
├─ 1. 函数入口
│ ├─ 参数:const K& key (目标键)
│ └─ 参数:const V& NewValue (新值)
│
├─ 2. 查找目标节点
│ └─ Node* target = Find(key)
│ ├─ 调用查找算法
│ └─ 时间复杂度:O(log n)
│
├─ 3. 存在性检查
│ └─ if (target == nullptr)
│ ├─ 未找到键 → return false
│ └─ 终止流程
│
├─ 4. 值更新操作
│ └─ target→_kv.second = NewValue
│ ├─ 直接修改节点数据
│ └─ 时间复杂度:O(1)
│
├─ 5. 返回结果
│ └─ return true
│
└─ 6. 算法特性
├─ 时间复杂度:O(log n) 主导因素为Find操作
├─ 空间复杂度:O(1)
└─ 关键路径示例:
更新key=20的值:
1. Find(20) → 找到节点B
2. B→value = "NewValue"
3. return true
2. 函数代码
bool UpDate(const K& key, const V& NewValue)
{
Node* target = Find(key);
if (!target) return false;
target->_kv.second = NewValue;
return true;
}
4.3 插入操作
1. 函数设计分析
Insert算法
├─ 1. 空树处理
│ └─ if (_root == nullptr)
│ ├─ 创建新根节点
│ └─ return true
│
├─ 2. BST标准插入
│ ├─ 循环查找插入位置
│ │ ├─ parent指针跟踪
│ │ ├─ 左子树遍历 (kv.first < cur)
│ │ └─ 右子树遍历 (kv.first > cur)
│ ├─ 发现重复键 → return false
│ └─ 创建新节点并链接
│ ├─ parent→left/right = cur
│ └─ cur→parent = parent
│
├─ 3. 平衡因子更新循环
│ │ (while parent != nullptr)
│ │
│ ├─ 3.1 更新规则
│ │ ├─ 插入左子树 → parent→_bf--
│ │ └─ 插入右子树 → parent→_bf++
│ │
│ ├─ 3.2 平衡状态判断
│ │ ├─ Case1: bf == 0
│ │ │ └─ break (高度不变)
│ │ ├─ Case2: bf == ±1
│ │ │ ├─ cur = parent
│ │ │ └─ parent = parent→parent (继续向上更新)
│ │ └─ Case3: bf == ±2 → 进入旋转调整
│ │
│ └─ 3.3 旋转调整分支
│ ├─ 右子树过重 (bf=+2)
│ │ ├─ 右右失衡 (cur→_bf=+1) → RotateL
│ │ └─ 右左失衡 (cur→_bf=-1) → RotateRL
│ └─ 左子树过重 (bf=-2)
│ ├─ 左左失衡 (cur→_bf=-1) → RotateR
│ └─ 左右失衡 (cur→_bf=+1) → RotateLR
│
├─ 4. 旋转后处理
│ ├─ 重置相关节点平衡因子
│ ├─ 调整祖父节点指针
│ └─ break退出更新循环
│
└─ 5. 返回结果
└─ return true
关键路径示例:
插入30(触发左旋)
1. parent=20, cur=25 → parent→_bf++
2. parent=20→_bf=1 → 继续向上
3. parent=30, cur=20 → parent→_bf++
4. parent=30→_bf=2 → 触发RotateL
5. 旋转后重置20和30的bf为0
2. 函数代码
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
parent = cur;
if (kv.first < cur->_kv.first)
cur = cur->_left;
else if (kv.first > cur->_kv.first)
cur = cur->_right;
else
return false; // 已存在,不插入
}
cur = new Node(kv);
if (kv.first < parent->_kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent;
// 更新平衡因子
while (parent)
{
if (cur == parent->_left)
parent->_bf--;
else
parent->_bf++;
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == 1 || parent->_bf == -1)
{
cur = parent;
parent = parent->_parent;
}
else if (parent->_bf == 2 || parent->_bf == -2)
{
// 需要旋转
if (parent->_bf == 2)
{
if (cur->_bf == 1)
RotateL(parent);
else
RotateRL(parent);
}
else
{
if (cur->_bf == -1)
RotateR(parent);
else
RotateLR(parent);
}
break; // 旋转后平衡,退出循环
}
else
{
assert(false); // 不可达
}
}
return true;
}
五、测试函数
5.1 测试代码
#include "AVLTree.h"
void TestAVLTree()
{
// 创建AVL树
AVLTree<int, string> foodTree;
// 测试插入功能
cout << "******插入*****" << endl;
cout << "插入10(Apple): " << foodTree.Insert({ 10, "Apple" }) << endl;
cout << "插入20(Banana): " << foodTree.Insert({ 20, "Banana" }) << endl;
cout << "插入30(Cherry): " << foodTree.Insert({ 30, "Cherry" }) << endl; // 触发左旋
cout << "重复插入20: " << foodTree.Insert({ 20, "Duplicate" }) << endl; // 测试重复插入
cout << endl;
// 测试遍历功能
cout << "******遍历******" << endl;
cout << "中序遍历结果: ";
foodTree.InorderPrint(foodTree.Find(10)); // 从根节点开始遍历
cout << endl;
// 测试查找功能
cout << "******查找******" << endl;
auto node20 = foodTree.Find(20);
cout << "查找20: " << (node20 ? "找到" : "未找到")
<< ",值=" << (node20 ? node20->_kv.second : "N/A") << endl;
auto node99 = foodTree.Find(99);
cout << "查找99: " << (node99 ? "找到" : "未找到") << endl;
cout << endl;
cout << endl;
// 测试修改功能
cout << "******修改******" << endl;
cout << "修改20→Mango: " << foodTree.UpDate(20, "Mango") << endl;
cout << "修改99→XXX: " << foodTree.UpDate(99, "XXX") << endl;
cout << endl;
// 验证修改结果
cout << "******修改结果******" << endl;
auto updatedNode = foodTree.Find(20);
cout << "20的新值: " << (updatedNode ? updatedNode->_kv.second : "N/A") << endl;
cout << endl;
// 平衡性检查
cout << "******平衡性******" << endl;
cout << "树是否平衡: " << (foodTree.IsBalance(foodTree.Find(10)) ? "是" : "否") << endl;
cout << endl;
}
int main()
{
TestAVLTree();
return 0;
}
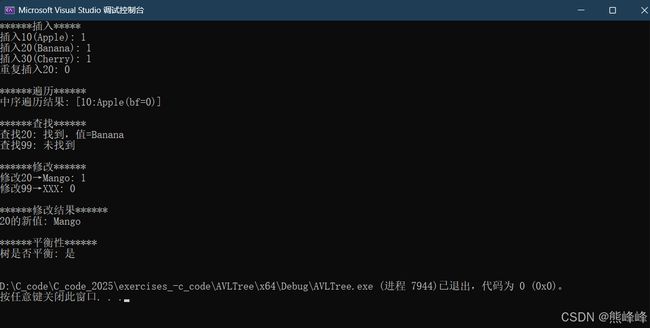
5.2 输出结果
**1. 预期输出结果
******插入*****
插入10(Apple): 1
插入20(Banana): 1
插入30(Cherry): 1
重复插入20: 0
******遍历******
中序遍历结果: [10:Apple(bf=0)] [20:Banana(bf=0)] [30:Cherry(bf=0)]
******查找******
查找20: 找到,值=Banana
查找99: 未找到
******修改******
修改20→Mango: 1
修改99→XXX: 0
******修改结果******
20的新值: Mango
******平衡性******
树是否平衡: 是
六、总结
6.1 优势分析
- 严格平衡保证O(log n)时间复杂度
- 适合读密集型场景
可作为其他数据结构的基础(这里主要是对下一节的红黑树的模拟实现做铺垫)
6.2 应用场景
- 数据库索引
- 内存数据库
- C++ STL的map/set实现基础
6.3 复杂度对比
| 操作 | 平均复杂度 | 最坏复杂度 |
|---|---|---|
| 查找 | O(log n) | O(log n) |
| 插入 | O(log n) | O(log n) |
| 删除 | O(log n) | O(log n) |
AVL树通过精巧的旋转策略实现了高效的自平衡,是计算机科学中平衡树结构的经典实现方案。
七、完整代码
7.1 AVLTree.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS
#include 7.2 Test.cpp
#include "AVLTree.h"
void TestAVLTree()
{
// 创建AVL树
AVLTree<int, string> foodTree;
// 测试插入功能
cout << "******插入*****" << endl;
cout << "插入10(Apple): " << foodTree.Insert({ 10, "Apple" }) << endl;
cout << "插入20(Banana): " << foodTree.Insert({ 20, "Banana" }) << endl;
cout << "插入30(Cherry): " << foodTree.Insert({ 30, "Cherry" }) << endl; // 触发左旋
cout << "重复插入20: " << foodTree.Insert({ 20, "Duplicate" }) << endl; // 测试重复插入
cout << endl;
// 测试遍历功能
cout << "******遍历******" << endl;
cout << "中序遍历结果: ";
foodTree.InorderPrint(foodTree.Find(10)); // 从根节点开始遍历
cout << endl;
cout << endl;
// 测试查找功能
cout << "******查找******" << endl;
auto node20 = foodTree.Find(20);
cout << "查找20: " << (node20 ? "找到" : "未找到")
<< ",值=" << (node20 ? node20->_kv.second : "N/A") << endl;
auto node99 = foodTree.Find(99);
cout << "查找99: " << (node99 ? "找到" : "未找到") << endl;
cout << endl;
// 测试修改功能
cout << "******修改******" << endl;
cout << "修改20→Mango: " << foodTree.UpDate(20, "Mango") << endl;
cout << "修改99→XXX: " << foodTree.UpDate(99, "XXX") << endl;
cout << endl;
// 验证修改结果
cout << "******修改结果******" << endl;
auto updatedNode = foodTree.Find(20);
cout << "20的新值: " << (updatedNode ? updatedNode->_kv.second : "N/A") << endl;
cout << endl;
// 平衡性检查
cout << "******平衡性******" << endl;
cout << "树是否平衡: " << (foodTree.IsBalance(foodTree.Find(10)) ? "是" : "否") << endl;
cout << endl;
}
int main()
{
TestAVLTree();
return 0;
}
看到这里我们的AVL树的基础操作模拟实现篇就结束了,本节主要是为了给下一篇红黑树做铺垫,后面还会更新更加精彩的红黑树模拟实现,有兴趣的可以关注一下博主,感谢大家的观看。