期望-pku-oj-1055:Tree

题目链接：

http://poj.openjudge.cn/practice/1055/

题目意思：

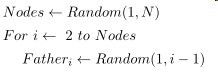给出的树最大节点个数为n的情况下，求树上点深度的期望。

解题思路：

数学期望公式的推导。

自己先画下nodes=1时 p[1]=1

nodes=2时，p[2]=0.5*1+0.5*2=3/2

nodes=3时，p[3]=11/6

nodes=4时，p[4]=50/24

nodes=5时，p[5]=274/120

.......其实p[n]就是调和级数h[n]=1+1/2+1/3+1/4+...1/n.啊。。。当时智商没看出来。。。。

正规推法：

记f[i]为第i个节点的深度期望，则放第i个节点时，前面的树的结构上有i-1个节点，第i个节点作为每个节点的儿子概率相同都为1/i-1.f[i]=1/(i-1)*(f[1]+1)+(i-1)*(f[2]+1)+...1/(i-1)*(f[i-1]+1)=1+1/(i-1)*sigma(f[k])(k从1到i-1);

记前i个节点的平均期望为E[i],则E[i]=sigma(f[k])/i(k从1到i).

则f[i]=E[i-1]+1. 则E[i]=(f[1]+f[2]+..+f[i-1])+f[i])/i=((i-1)*E[i-1]+E[i-1]+1)/i=E[i-1]+1/i; 所以E[i]=1+1/2+1/3+1/4+.....1/i.

则ans=sigma(E[k])/n(k从1到n)

可以推出ans=(n+1)/n*h[n]-1. //h[n]为调和级数

当n很小时，可以直接暴力。当n很大时，h[n]趋近与ln(n)+C C为欧拉常数(大概0.577216），可以暴力打出来。

代码：

 

#include<iostream>

#include<cmath>

#include<cstdio>

#include<sstream>

#include<cstdlib>

#include<string>

#include<cstring>

#include<algorithm>

#include<vector>

#include<map>

#include<set>

#include<stack>

#include<list>

#include<queue>

#include<ctime>

#include<bitset>

#define eps 1e-6

#define INF 0x3f3f3f3f

#define PI acos(-1.0)

#define ll __int64

#define LL long long

#define lson l,m,(rt<<1)

#define rson m+1,r,(rt<<1)|1

#define M 1000000007

#pragma comment(linker, "/STACK:1024000000,1024000000")

using namespace std;



#define Maxn 1100000



double h[Maxn];



int main()

{

    int m=1000000;

    h[1]=1;



    for(int i=2;i<=m;i++)

        h[i]=h[i-1]+1.0/(i*1.0);



    double la=h[m]-log(m*1.0); //求出欧拉常数

    //printf("%lf\n",la);

    LL n;

   // printf("%lf\n",13.0/9.0);



    while(~scanf("%lld",&n))

    {

        if(n<=m)  //直接算

            printf("%.8lf\n",(n+1.0)/(n*1.0)*h[n]-1.0);

        else

        {

            double temp=log(n*1.0)+la; //用等价的极限近似值代替

            printf("%.8lf\n",(n+1.0)/(n*1.0)*temp-1.0);

        }

    }

   return 0;

}