蓝桥杯 X进制减法
问题描述
进制规定了数字在数位上逢几进一。
X 进制是一种很神奇的进制, 因为其每一数位的进制并不固定！例如说某 种 X 进制数, 最低数位为二进制, 第二数位为十进制, 第三数位为八进制, 则 X 进制数 321 转换为十进制数为 65 。
现在有两个 X 进制表示的整数 A 和 B, 但是其具体每一数位的进制还不确 定, 只知道 A 和 B 是同一进制规则, 且每一数位最高为 N 进制, 最低为二进 制。请你算出 A−B 的结果最小可能是多少。
请注意, 你需要保证 A 和 B 在 X 进制下都是合法的, 即每一数位上的数 字要小于其进制。
输入格式
第一行一个正整数 N, 含义如题面所述。
第二行一个正整数 Ma, 表示 X 进制数 A 的位数。
第三行 Ma 个用空格分开的整数, 表示 X 进制数 A 按从高位到低位顺序各 个数位上的数字在十进制下的表示。
第四行一个正整数 Mb, 表示 X 进制数 B 的位数。
第五行 Mb 个用空格分开的整数, 表示 X 进制数 B 按从高位到低位顺序各 个数位上的数字在十进制下的表示。
请注意, 输入中的所有数字都是十进制的。
输出格式
输出一行一个整数, 表示 X 进制数 A−B 的结果的最小可能值转换为十进 制后再模 1000000007 的结果。
样例输入
11
3
10 4 0
3
1 2 0
样例输出
94
样例说明
当进制为: 最低位 2 进制, 第二数位 5 进制, 第三数位 11 进制时, 减法 得到的差最小。此时 A 在十进制下是 108,B 在十进制下是 14 , 差值是 94。
评测用例规模与约定
对于 30% 的数据, N≤10;Ma,Mb≤8.
对于 100% 的数据, 2≤N≤1000;1≤Ma,Mb≤100000;A≥B.
将 X 进制数 321 转换为十进制数 65：
在这个例子中，X 进制数的每一位的进制如下：
-
最低位（个位）是二进制（基数为 2）
-
第二位是十进制（基数为 10）
-
第三位是八进制（基数为 8）
因此，X 进制数 321 的每一位的权重计算如下：
-
第三位（百位）：3
这一位的基数是 8（八进制），所以它的权重是 3×(10×2)=3×20=60。 -
第二位（十位）：2
这一位的基数是 10（十进制），所以它的权重是 2×2=4。 -
最低位（个位）：1
这一位的基数是 2（二进制），所以它的权重是 1×1=1。
将这些权重相加：
60+4+1=65
因此，X 进制数 321 转换为十进制数就是 65。
进制的基本原理
在常规的进制（如十进制、二进制）中，每一位的权重是固定的。例如：
-
在十进制中，每一位的权重是
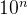（n 是从右到左的位数，从 0 开始）。 -
在二进制中，每一位的权重是
。
但在 X 进制中，每一位的基数可能不同，因此每一位的权重需要动态计算。
X 进制数的每一位的权重是由其右侧所有位的基数相乘得到的：
-
举个例子：
假设有一个 X 进制数，其各位的基数如下：
-
最低位（个位）：基数 b0=2
-
第二位（十位）：基数 b1=10
-
第三位（百位）：基数 b2=8
-
其右侧的基数分别是 b1=10和 b0=2。
-
因此，第三位的权重是 d2×(b1×b0)=d2×(10×2)=d2×20。
-
第三位的值每增加 1，相当于增加了 20 个单位的十进制值。
-
这是因为右侧的基数 b1=10 和 b0=2 共同决定了第三位的“单位”是 20
保证 A−B的值最小 的核心逻辑是通过 动态选择每一位的进制，使得 A 的值尽可能小，同时 B 的值尽可能大
在代码中，每一位的进制选择为：
ll current_base = max(2ll, max(a[i], b[i]) + 1);
-
max(a[i], b[i]) + 1：确保进制大于当前位 A 和 B 的数字中的最大值。 -
max(2ll, ...)：确保进制至少为 2（题目要求最低为二进制）。
这种选择方式的意义在于：
-
对于 A：
-
如果 A 的当前位数字较大，选择较小的进制可以减小 A 的值。
-
例如，如果 a[i]=10，选择进制为 11 而不是更大的数，可以减小 A 的值。
-
-
对于 B：
-
如果 B 的当前位数字较小，选择较大的进制可以增大 B 的值。
-
例如，如果 b[i]=1，选择进制为 11 而不是更小的数，可以增大 B 的值。
-
#include
#include
#include
using namespace std;
typedef long long ll;
int n;
int ma, mb;
const int N = 1e5+10;
ll a[N], b[N]; //不能直接写1e5+10 ，这样写是浮点型
ll base=1, ans, mod=1e9+7;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
cin>>ma;
for(int i=ma; i>=1; i--) cin>>a[i]; //倒序
cin>>mb;
for(int i=mb; i>=1; i--) cin>>b[i]; //倒序
for(int i=1; i<=ma; ++i)
{
//当前位的进制
//字面量表示法：将 2 明确指定为 long long 类型的常量
ll current_base = max(2ll, max(a[i], b[i])+1);
//一个X进制的数转为十进制 - 另一个X进制的数转为十进制 等价于
//一个X进制数的每一位与另一个X进制数的每一位的差 转为十进制 的和
ans += (a[i]-b[i])*base; //第一位的权重是1
ans %= mod;
//每次更新ans和base之后，都对1e9+7取模，防止数值溢出
base *= current_base;
base %= mod;
}
cout<
补充：
在 C++ 中，还有其他类似的字面量后缀：
u：表示unsigned int，例如2u。
ul：表示unsigned long，例如2ul。
ull：表示unsigned long long，例如2ull。
f：表示float，例如2.0f。
L：表示long double，例如2.0L。