LeetCode Hot 100 - 矩阵 | 73.矩阵置零、54.螺旋矩阵、48.旋转图像、240.搜索二维矩阵II

73.矩阵置零

新建两个boolean数组记录该行或列是否出现0，再使用数组更新矩阵。

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length; 
        int n = matrix[0].length;
        boolean[] row = new boolean[matrix.length];
        boolean[] col = new boolean[matrix[0].length];
        for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ; j++){
                if( matrix[i][j] == 0 ){
                    row[i] = true;
                    col[j] = true;
                }
            }
        }
         for(int i = 0 ; i < m ; i++){
            for(int j = 0 ; j < n ; j++){
                if( row[i] || col[j] ){
                    matrix[i][j] = 0 ;
                }
            }
        }
    }
}

优化空间复杂度：使用矩阵的第一行和第一列当做数组记录，要提前利用两个变量将第一行或第一列是否有0进行记录，最后使用该变量对第一行和第一列进行处理。

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        boolean row = false;
        boolean col = false;
        for(int i = 0 ; i

54.螺旋矩阵

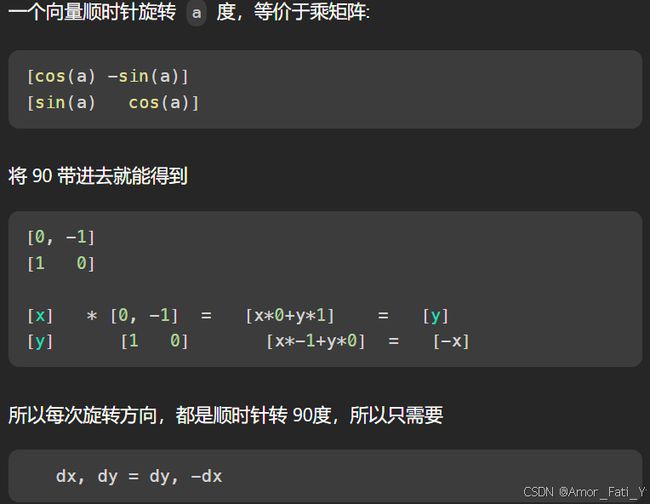
利用旋转矩阵

用x，y标记当前位置，dx和dy为当前移动方向，用Integer.MIN_VALUE标记记录过的元素。

若下一步超出数组范围或遇到记录过的元素，则将方向顺时针调整90度。

class Solution {
    public List spiralOrder(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        List res = new ArrayList<>();
        int x = 0 ; int y = 0;
        int dx = 0 ; int dy = 1;
        int temp = 0;
        for(int i = 0 ; i=m || y+dy<0 || y+dy>=n || matrix[x+dx][y+dy]==Integer.MIN_VALUE){
                temp = dx;
                dx = dy;
                dy = -temp;
            }
            x += dx;
            y += dy;
        }
        return res;
    }
}

48.旋转图像

向右旋转90度相当于 水平旋转后 在进行主对角线旋转；

水平旋转是第一行和最后一行交换，

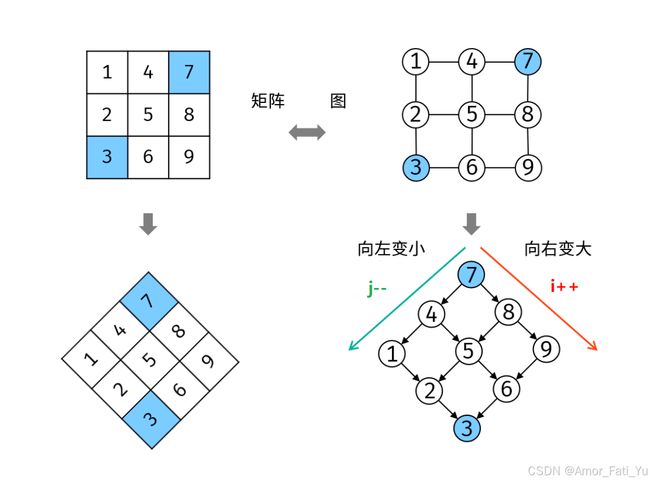
主对角线是 [i][j] 交换 [j][i] ，只需要交换上半部分（j

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        for(int i = 0 ; i

240.搜索二维矩阵II

如图所示，将矩阵右上角作为顶点，可以将关系看做，小于当前值（i，j）的数在左边（即向左的列，j--），大于的数在右边（即向下的行 i++），依据此规律在矩阵中查找。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int i = 0 ;
        int j = matrix[0].length-1;
        while(i<=matrix.length-1 && j>=0){
            if(matrix[i][j]target) j--;
            else return true;
        }
        return false;
    }
}