[置顶] LOD层次细节算法-大规模实时地形的绘制
背景
在介绍层次细节算法之前,先来看两幅图片。
这两幅图片是用层次细节算法也即LOD算法绘制的地形网格。为了更清晰的看清地形网格的结构,我没有给其贴上纹理。这两幅图片看上去给人第一感觉就是分辨率不同,图一分辨率较低,图二分辨率很高。图一图二是由同一个程序生成的,图一时在调节系数为1的情况下生成的,图二是在调节系数为25的情况下生成的。为了增加对比度,我故意把两幅图片的分辨率调节的差别很大。这个地形网格如果达到全分辨率的话将会是513像素*513像素。然而读者看到的图片并没有达到全分辨率。为什么呢?大家想一下,在现实世界中,人眼的视角是有一个范围的并不能看到360度范围的场景;随着视线的往远处移动,看到的东西越来越模糊;大家在想一下另外一个问题,把图片贴到一个物体上,如果这个物体的表面是平的,那么任务肯定非常容易完成,如果物体表面凸凹不平,那么你就不能把图片直接贴在上面,你必须把图片简称小的片段然后在艰难的贴在物体表面。同理层次细节算法就是模拟上述现实场景的技术,只不过我们将换一套专有名词来描述。上述地形网格在满足下面三个条件时候被绘制,一,不在照相机视景体内的网格部分将不会被绘制;二,距离相机视点远的地方网格以低分辨率来绘制,近的地方以高分辨率来绘制;三,粗糙的部分以高分辨率绘制,平坦的部分以较低的分辨率来绘制。这三个条件合称节点评价系统。
地形高程图
在层次细节地形绘制的过程中,每一个顶点坐标(x,y,z)被分为两部分处理,(x,z)与y两个部分。至于为什么这样做,当你看完本篇文章之后你就会明白。在OpenGL里面Y轴是垂直向上的,因此顶点的y坐标值代表顶点的高度。高程图就是存储y坐标值得,其中一种方法就是使用raw格式的文件。raw格式文件是8为的,也就是说把raw格式的图片看成width*hight大小的矩形的话,其中每个元素表示一个8位的数据,范围是0到256。在层次细节算法中要求地形的大小必须是正方形,而且必须满足边长的像素数为(2的n次方)+1;后文大家会明白为什么会有这两个限制。本文我们使用.raw格式的高程图,其制作方法有很多,本文介绍一种最简单的方法,用photoshop生成,如果要想生成自己想要的那种地形需要使用专业的方法来生成高程图,本文使用的是随机生成的高程图。方法很简单,打开PS快捷键crtl+N新建一个513*513像素大小的项目,确定后从工具栏里选择滤镜->渲染->分层云彩,然后存储为选择.raw格式,至此高程图就完成了。下面给出加载高程图的程序代码:
void GLLod::loadRawFile(LPSTR strName, int nSize)
{
FILE *pFile=NULL;
pFile=fopen(strName,"rb");
if(pFile==NULL)
{
MessageBox(NULL,TEXT("不能打开高度图文件"),TEXT("错误"),MB_OK);
return;
}
fread(pHeightMap,1,nSize,pFile);
int result=ferror(pFile);
if(result)
{
MessageBox(NULL,TEXT("读取数据失败"),TEXT("错误"),MB_OK);
}
fclose(pFile);
}
从高程图中得到坐标(x,z)处的高度值的程序代码:
int GLLod::getRawHeight(int x, int z)
{
int xx=x%(map_size+1);
int zz=z%(map_size+1);
if(!pHeightMap) return 0;
return pHeightMap[xx+(zz*(map_size+1))];
}
层次细节算法(LOD算法)
现在要步入正题了,我将会向大家介绍层次细节算法的原理。LOD算法采用的是四叉树的结构来处理的。
我们看上图,网格一是最初始的没有分割的正方形,其边长是![]() 如果以像素表示边长的话那么边上有
如果以像素表示边长的话那么边上有![]() 个像素。那么在这里我们可以看出每一个网格的边长是5个像素,若每个像素间的距离为一的话,那么每个网格的边长是4,下文中我们默认每个像素间的距离唯一。将网格一等分为4个小网格,那么这四个小网格是原网格的四个儿子节点,继续划分,图二中的每个儿子网格继续划分为四个儿子。我们可以有选择的划分某些网格,每个网格一旦划分的话,就必需划分为四个相等的小网格。这种划分方法很明显是符合四叉树的,只不过这个四叉树每个节点要么有四个儿子,要么没有儿子。上面描述的网格是在x-z平面上,至此还没有考虑y坐标呢。等划分到一定标准的时候就会在此基础上考虑y坐标,这个时候就可以渲染了,不过距离这一步还有很远的距离。这个划分结束的标准就是前文中所说的节点评价系统。下面我们就来详细讲述节点评价系统。
个像素。那么在这里我们可以看出每一个网格的边长是5个像素,若每个像素间的距离为一的话,那么每个网格的边长是4,下文中我们默认每个像素间的距离唯一。将网格一等分为4个小网格,那么这四个小网格是原网格的四个儿子节点,继续划分,图二中的每个儿子网格继续划分为四个儿子。我们可以有选择的划分某些网格,每个网格一旦划分的话,就必需划分为四个相等的小网格。这种划分方法很明显是符合四叉树的,只不过这个四叉树每个节点要么有四个儿子,要么没有儿子。上面描述的网格是在x-z平面上,至此还没有考虑y坐标呢。等划分到一定标准的时候就会在此基础上考虑y坐标,这个时候就可以渲染了,不过距离这一步还有很远的距离。这个划分结束的标准就是前文中所说的节点评价系统。下面我们就来详细讲述节点评价系统。
节点评价系统
相机裁剪上面我们划分了网格一,直至网格三,但是那个划分是盲目的,接下来我们就必需按照一定的标准有目的的划分。来看几副图片。
途中的红色线代表照相机(也可以理解为人的眼睛)的视野范围,及时只有一小部分在相机视野内,我们就需要对其进行划分,显然图一的正方形在视野内,对其划分得到图二中的网格,这个时候可以发现图二中的最右边的两个儿子网格仍然在视野内,因此对其继续划分,最左边两个儿子网格不在视野内,因此不必划分也即被裁剪掉了,于是得到了图三中的网格。现在呈现给读者的是平面的,实际上考虑y轴坐标的话,网格节点是一个三维的,为了方便我们以平面的方式来阐述,实际上是三维的。那么如何进行三维的裁剪呢?在笔者的前一篇文章《3D坐标系、矩阵运算、视景体与裁剪》中对其算法进行了描述,这里只给出代码。
int GLFrustum::isAabbInFrustum( AABB &aabb)
{
//aabb是一个AABB包围盒
calculateFrustumPlanes();//计算平截头体的六个面的方程
bool insect=false;//相机裁剪的标志
for(int i=0;i<6;i++)
{
//接下来3个if语句是轴分离的方法调整aabb包围盒
if(g_frustumPlanes[i][0]<0.0f)
{
int temp=aabb.min[0];
aabb.min[0]=aabb.max[0];
aabb.max[0]=temp;
}
if(g_frustumPlanes[i][1]<0.0f)
{
int temp=aabb.min[1];
aabb.min[1]=aabb.max[1];
aabb.max[1]=temp;
}
if(g_frustumPlanes[i][2]<0)
{
int temp=aabb.min[2];
aabb.min[2]=aabb.max[2];
aabb.max[2]=temp;
}
if((g_frustumPlanes[i][0]*aabb.min[0]+g_frustumPlanes[i][1]*aabb.min[1]+g_frustumPlanes[i][2]*aabb.min[2]+g_frustumPlanes[i][3])>0.0f)
{
return 0;//不可见
}
if((g_frustumPlanes[i][0]*aabb.max[0]+g_frustumPlanes[i][1]*aabb.max[1]+g_frustumPlanes[i][2]*aabb.max[2]+g_frustumPlanes[i][3])>=0.0f)
{
insect=true;//裁剪
}
}
if(insect) return 1;//裁剪
return 2;//完全可见
}
这其中的calculateFrustumPlanes();是用来计算平截头体的六个面的方程读者可以点击这里了解详情。
视点距离上面的相机裁剪部分说在视野范围内的继续划分,那么视野内的那部分是不是一直继续划分呢?当然不是,过度的划分并不会带来视觉上的改观而会增加GPU的处理负担,试想如果有1000万个顶点的话,那处理起来是非常消耗GPU的。根据常识,在现实世界中我们看远处的物体会感觉到模糊,看近处的会感觉比较清晰,同样LOD算法里也是采用这个理念,距离视点远的网格节点就不必要继续划分,而近处的网格则要继续划分。
如图一个小兔子的眼睛看着右上角的网格,我们定义距离L是眼睛到网格中心的距离,d是目标网格的边长。满足条件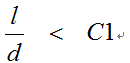 的时候网格继续划分,否则不需要继续划分。C1是一个可以根据实际渲染情况调节的值因子。图一 图二就是不同调节因子所形成的两幅地形网格。
的时候网格继续划分,否则不需要继续划分。C1是一个可以根据实际渲染情况调节的值因子。图一 图二就是不同调节因子所形成的两幅地形网格。
粗糙程度
在物体粗糙的部分需要继续划分以更好的显示,而平坦的部分则不需要做过多的划分,比如一个平面直接贴纹理就行了,做过多的划分是没有意义的。
那么怎么定义网格的粗糙程度呢?如图所示,如果在xz平面考虑问题的话,那么网格的每个节点的边都是在一个平面上的,如果考虑y坐标的话原来是直线的边会变成曲线,我们以每个网格四条边的起伏程度和中心点的起伏程度的最大值来定义网格的粗糙度。举个例子在上图中dh4的值是那条边的两个顶点的y坐标值相加再除以2以后减去边的中点的y坐标值得到dh4,这个dh4就是所在边的起伏度,同样方法计算dh1 dh2 dh3。中心点需要计算两次,因为中心点所在的边有两条,分别是对应的两个对角线。这6个值计算出来后选择其中最大的作为粗糙度。设粗糙度为DHmax,那么满足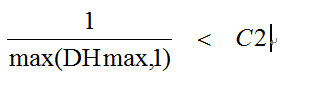 条件时继续划分,否则不划分。其中C2是可以调节的因子。这个条件可以和上一个条件合并得到
条件时继续划分,否则不划分。其中C2是可以调节的因子。这个条件可以和上一个条件合并得到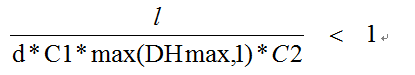 。
。
总结来说if(相机裁剪通过&&视点-粗糙值合适) then 划分节点,否则不划分。
消除裂缝如果仅仅做到上面所说的是不是就可以渲染地形了呢?答案是否定的,因为这样会产生裂缝。什么是裂缝呢?我们来看两幅图片就可以知道了。
地形一
地形二
为了方便大家观察,每一副图片部分网格以线框的模式渲染另一部分以填充的方式渲染。图一是正常的,图二却有许多列缝。这是什么原因呢?为了弄明白这一点我们先放一放,看另外一个问题,网格是怎么渲染的呢?
如图是一个即将送往3D API渲染的网格节点。共有九个节点,中心点是0点,另外还有8个点。在OpenGL里这个网格将会以三角形扇的方式进行渲染,比如032是一个三角形,021又是一个三角形。但是这样渲染是有问题的,看接下来的图片:
在上面这个图中左右两个网格的划分层次相差为1,也就是右侧的网格比左侧的多划分一次。这时候问题出现了,当以顶点1 2 3渲染三角形和以顶点2 4 5渲染三角形以及以顶点5 4 3渲染三角形时候就出现了裂缝。图上面是在xz平面上看不出问题,但是当给顶点赋予y坐标值的时候问题就出现了,因为点4可能和点2 点3不在一个高度,所以点2 点4点3组成的可能是一条折线。假如点2 点3的高度相同,点4比点2 点3 高,那么点2 点3 点4便组成了一个三角形,这个三角形就是地形二上面的裂缝。大家可以看下比较大的裂缝会发现正好是个三角形,这就是很多诸如点2 点3 点4组成的三角形裂缝。那么怎么解决这个问题呢?可以在点1 点4之间增加一条线段,这个处理起来比较麻烦,本文采取的是将点4点5组成的线段取消,也即删除点4,这个时候裂缝便会消失,如地形一那样。但是我们忽略了一个问题,这个还是比较棘手的问题,我们再看一张图片:
在这幅图里面,右侧的网格比左侧的网格多划分了2次,这个时候顶点3 顶点6 顶点5 顶点4组成的边比先前那个例子更加复杂了。即使删除点5,点3 点6 点4仍然可能组成一个三角形裂缝。点6不能删除,因为点6是正方形网格的顶点,删除它就等于删除网格了,所以只能删除边的中点。这下怎么办呢?如果有一种方法保证左右两侧的两个正方形网格划分层次相差小于等于1,那么就可以按照前文所说的那样通过删除点来消除三角形裂缝。能做到这一点吗?答案是肯定的。假设左侧的网格划分值为f1右侧的父亲网格为f2当f2的父亲网格需要划分的时候必须保证f1也划分。即满足表达式;f2<f1<1的情况下可以被划分。也即
从视点做垂直于xz平面的直线交予xz面与O点。此时有 代入后得到
代入后得到
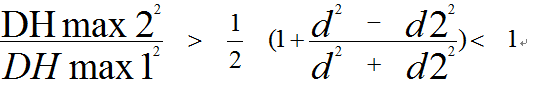 也就是说DHmax2>DHmax1的话就可以满足上式,从而消除三角形裂缝。如何使得DHmax2>DHmax1呢?可以这样做,对于左边的正方形网格求紧贴其四条边的边长为其一半的8个小正方形的DHmax值,再与其自身的DHmax比较,并将最大值当初该网格的DHmax值。这样就可以保证右侧的小正方形父亲被划分时候左侧的大的正方形网格也被划分,这样就可以保证他们的划分层次相差小于等于1。如此便不会出现三角形裂缝。调整DHmax的函数代码是:
也就是说DHmax2>DHmax1的话就可以满足上式,从而消除三角形裂缝。如何使得DHmax2>DHmax1呢?可以这样做,对于左边的正方形网格求紧贴其四条边的边长为其一半的8个小正方形的DHmax值,再与其自身的DHmax比较,并将最大值当初该网格的DHmax值。这样就可以保证右侧的小正方形父亲被划分时候左侧的大的正方形网格也被划分,这样就可以保证他们的划分层次相差小于等于1。如此便不会出现三角形裂缝。调整DHmax的函数代码是:
void GLLod::modifyDHMatrix()
{
int edgeLength=2;
while(edgeLength<=map_size)
{
int halfEdgeLength=edgeLength>>1;
int halfChildEdgeLength=edgeLength>>2;
for(int z=halfEdgeLength;z<map_size;z+=edgeLength)
{
for(int x=halfEdgeLength;x<map_size;x+=edgeLength)
if(edgeLength==2)
{
int DH6[6];
DH6[0]=abs(((getRawHeight(x-halfEdgeLength,z+halfEdgeLength)+getRawHeight(x+halfEdgeLength,z+halfEdgeLength))>>1)-getRawHeight(x,z+halfEdgeLength));
DH6[1]=abs(((getRawHeight(x+halfEdgeLength,z+halfEdgeLength)+getRawHeight(x+halfEdgeLength,z-halfEdgeLength))>>1)-getRawHeight(x+halfEdgeLength,z));
DH6[2]=abs(((getRawHeight(x-halfEdgeLength,z-halfEdgeLength)+getRawHeight(x+halfEdgeLength,z-halfEdgeLength))>>1)-getRawHeight(x,z-halfEdgeLength));
DH6[3]=abs(((getRawHeight(x-halfEdgeLength,z+halfEdgeLength)+getRawHeight(x-halfEdgeLength,z-halfEdgeLength))>>1)-getRawHeight(x-halfEdgeLength,z));
DH6[4]=abs(((getRawHeight(x-halfEdgeLength,z-halfEdgeLength)+getRawHeight(x+halfEdgeLength,z+halfEdgeLength))>>1)-getRawHeight(x,z));
DH6[5]=abs(((getRawHeight(x+halfEdgeLength,z-halfEdgeLength)+getRawHeight(x-halfEdgeLength,z+halfEdgeLength))>>1)-getRawHeight(x,z));
int DHMax=DH6[0];
for(int i=1;i<6;i++)
{
if(DHMax<DH6[i])
DHMax=DH6[i];
}
setDHMatrix(x,z,DHMax);
}
else
{
int DH14[14];
int numDH=0;
int neighborX;
int neighborZ;
neighborX=x-edgeLength;
neighborZ=z;
if(neighborX>0)
{
DH14[numDH]=getDHMatrix(neighborX+halfChildEdgeLength,neighborZ-halfChildEdgeLength);
numDH++;
DH14[numDH]=getDHMatrix(neighborX+halfChildEdgeLength,neighborZ+halfChildEdgeLength);
numDH++;
}
neighborX=x;
neighborZ=z-edgeLength;
if(neighborZ>0)
{
DH14[numDH]=getDHMatrix(neighborX-halfChildEdgeLength,neighborZ+halfChildEdgeLength);
numDH++;
DH14[numDH]=getDHMatrix(neighborX+halfChildEdgeLength,neighborZ+halfChildEdgeLength);
numDH++;
}
neighborX=x+edgeLength;
neighborZ=z;
if(neighborX<map_size)
{
DH14[numDH]=getDHMatrix(neighborX-halfChildEdgeLength,neighborZ-halfChildEdgeLength);
numDH++;
DH14[numDH]=getDHMatrix(neighborX-halfChildEdgeLength,neighborZ+halfChildEdgeLength);
numDH++;
}
neighborX=x;
neighborZ=z+edgeLength;
if(neighborZ<map_size)
{
DH14[numDH]=getDHMatrix(neighborX-halfChildEdgeLength,neighborZ-halfChildEdgeLength);
numDH++;
DH14[numDH]=getDHMatrix(neighborX+halfChildEdgeLength,neighborZ-halfChildEdgeLength);
numDH++;
}
DH14[numDH]=abs(((getRawHeight(x-halfEdgeLength,z+halfEdgeLength)+getRawHeight(x+halfEdgeLength,z+halfEdgeLength))>>1)-getRawHeight(x,z+halfEdgeLength));
numDH++;
DH14[numDH]=abs(((getRawHeight(x+halfEdgeLength,z+halfEdgeLength)+getRawHeight(x+halfEdgeLength,z-halfEdgeLength))>>1)-getRawHeight(x+halfEdgeLength,z));
numDH++;
DH14[numDH]=abs(((getRawHeight(x-halfEdgeLength,z-halfEdgeLength)+getRawHeight(x+halfEdgeLength,z-halfEdgeLength))>>1)-getRawHeight(x,z-halfEdgeLength));
numDH++;
DH14[numDH]=abs(((getRawHeight(x-halfEdgeLength,z+halfEdgeLength)+getRawHeight(x-halfEdgeLength,z-halfEdgeLength))>>1)-getRawHeight(x-halfEdgeLength,z));
numDH++;
DH14[numDH]=abs(((getRawHeight(x-halfEdgeLength,z-halfEdgeLength)+getRawHeight(x+halfEdgeLength,z+halfEdgeLength))>>1)-getRawHeight(x,z));
numDH++;
DH14[numDH]=abs(((getRawHeight(x+halfEdgeLength,z-halfEdgeLength)+getRawHeight(x-halfEdgeLength,z+halfEdgeLength))>>1)-getRawHeight(x,z));
numDH++;
int DHMax=DH14[0];
for(int i=1;i<14;i++)
{
if(DHMax<DH14[i])
DHMax=DH14[i];
}
setDHMatrix(x,z,DHMax);
}
}
edgeLength=edgeLength<<1;
}
}
生成地形网格的代码如下:
void GLLod::updateQuadTreeNode(int centerX, int centerZ,int edgeLength,int child)
{
if(edgeLength>2)
{
if(isObjectCulled(centerX,centerZ,edgeLength))
{
quadNode[centerX+centerZ*(map_size+1)].blend=2;
}
else
{
float fViewDistance,f;
int halfChildEdgeLength;
int childEdgeLength;
int blend;
int centerQuad[3];
centerQuad[0]=centerX;
centerQuad[2]=centerZ;
centerQuad[1]=getRawHeight(centerX,centerZ);
fViewDistance=frustum.distanceOfTwoPoints(centerQuad);
f=fViewDistance/(edgeLength*mfMinResolution*(max(mfDetailLevel*getDHMatrix(centerX,centerZ),1.0f)));
if(f<1.0f)
blend=1;
else
blend=0;
int temp=centerX+centerZ*(map_size+1);
quadNode[temp].blend=blend;
quadNode[temp].centerX=centerX;
quadNode[temp].centerY=centerQuad[1];
quadNode[temp].centerZ=centerZ;
quadNode[temp].child=child;
quadNode[temp].edgeLength=edgeLength;
if(blend==1)
{
int halfChildEdgeLength=edgeLength>>2;
int childEdgeLength=edgeLength>>1;
updateQuadTreeNode(centerX-halfChildEdgeLength,centerZ-halfChildEdgeLength,childEdgeLength,1);
updateQuadTreeNode(centerX+halfChildEdgeLength,centerZ-halfChildEdgeLength,childEdgeLength,2);
updateQuadTreeNode(centerX-halfChildEdgeLength,centerZ+halfChildEdgeLength,childEdgeLength,3);
updateQuadTreeNode(centerX+halfChildEdgeLength,centerZ+halfChildEdgeLength,childEdgeLength,4);
}
}
}
}
现在具体渲染的时候如何选择顶点还没讲,现在已经很晚了,以后再写吧。。
邮箱:[email protected]欢迎指出文中的错误之处。
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第1张图片](http://img.e-com-net.com/image/product/d0d9ec83378f498ca1a7351efdb3c0a4.png)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第2张图片](http://img.e-com-net.com/image/product/9e779aa5d59e4d958ef4ad55ef9bfaec.jpg)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第3张图片](http://img.e-com-net.com/image/product/9047e09b470c4616b0112d385718b2a9.png)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第4张图片](http://img.e-com-net.com/image/product/390cb52d609d49a2a588f29120caffed.png)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第5张图片](http://img.e-com-net.com/image/product/7dad7fb00078453a857a54d0284624fb.png)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第6张图片](http://img.e-com-net.com/image/product/f6a2976a9cab407b8acc151682c564f7.jpg)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第7张图片](http://img.e-com-net.com/image/product/01c38a38b7614c3a939e4e1c96d781da.jpg)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第8张图片](http://img.e-com-net.com/image/product/76ee5ea87e7a415ab54b52831a50eef3.jpg)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第9张图片](http://img.e-com-net.com/image/product/2f91045f70ce4fef8d8bb39a9c442686.png)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第10张图片](http://img.e-com-net.com/image/product/4861052b822f4598976e252535d0c92e.png)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第11张图片](http://img.e-com-net.com/image/product/ff4bed3970714efb942a2d6a6d973cc2.jpg)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第12张图片](http://img.e-com-net.com/image/product/30a200313ba045b3a8e3ec8c0c6ae272.jpg)
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第13张图片](http://img.e-com-net.com/image/product/36ac307873c047eebdd0d190f738ce06.jpg)

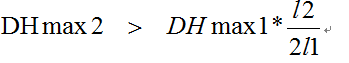
![[置顶] LOD层次细节算法-大规模实时地形的绘制_第14张图片](http://img.e-com-net.com/image/product/6490e60155544b9a89e2dbfe3d2eacaf.jpg)