旋转机械振动分析基础
振动分析基本概念
振动是一种动态量,其最简单的形式是简谐振动。简谐振动的振动量按余弦或正弦函数规律周期性变化,表达式为:
y = A sin ( ω t + φ ) y = A \sin(\omega t + \varphi) y=Asin(ωt+φ)
其中:
- y y y 为振动位移;
- A A A 为振动幅值,反映振动的大小;
- φ \varphi φ 为振动相位,反映信号在 t = 0 t = 0 t=0 时刻的初始状态;
- ω \omega ω 为圆频率, ω = 2 π f \omega = 2\pi f ω=2πf;
- f f f 为振动频率,反映振动动态变化的快慢程度;
- T T T 为周期, T = 1 f T = \frac{1}{f} T=f1。
振动监测中常用波形的正、负峰值差值作为振动幅值,称为峰峰值,记为 A pp A_{\text{pp}} App。而式中的 A A A 为半峰值,记为 A op A_{\text{op}} Aop。
为了完全描述一个振动信号,必须同时知道幅值、频率和相位这三个参数,它们被称为振动分析的三要素。
实际振动比简谐振动复杂得多,但任何复杂振动信号都可以分解为若干具有不同频率、幅值和相位的简谐分量的合成。
旋转机械振动分析离不开转速。通常用1x表示与转动频率相等的频率,称为工频(基频);0.5x、2x、3x等分别表示转动频率的0.5倍、2倍和3倍,称为半频、二倍频、三倍频。
通过快速傅立叶变换(FFT),可以求出复杂振动信号所含频率分量的幅值和相位。频谱分析已成为振动故障诊断的基本工具,其作用主要体现在:
- 不同故障对应不同的频率特征。例如,转子不平衡故障的频率为工频,汽流激振和油膜振荡等故障的频率为低频,电磁激振等故障的频率为高频。
- 多种故障的频率特征可能相似,因此频率特征不是故障判断的充分条件。需要结合过程参数和相关试验数据进行综合分析。
振动位移、速度和加速度
振动分析中除了使用振动位移外,还经常用到振动速度和加速度。通过以下公式可以相互转换:
- 速度: v = d y d t = ω A cos ( ω t + φ ) v = \frac{dy}{dt} = \omega A \cos(\omega t + \varphi) v=dtdy=ωAcos(ωt+φ)
- 加速度: a = d 2 y d t 2 = − ω 2 A sin ( ω t + φ ) a = \frac{d^2y}{dt^2} = -\omega^2 A \sin(\omega t + \varphi) a=dt2d2y=−ω2Asin(ωt+φ)
从上述公式可以看出:
- 振动位移、速度和加速度的频率相同,都可以用于振动监测。
- 在相同位移幅值下,频率越高,振动产生的交变应力越大,对设备的危害也越大。
- 振动速度和加速度的幅值同时反映了振动频率和位移幅值的影响,比单纯的位移幅值更全面。
- 振动加速度相位超前振动速度相位90°,振动速度相位超前振动位移相位90°。
- 同一种故障在振动位移、速度和加速度频谱中的表现不同。高频分量在速度和加速度频谱中会被“放大”,而低频分量在位移频谱中会被“放大”。
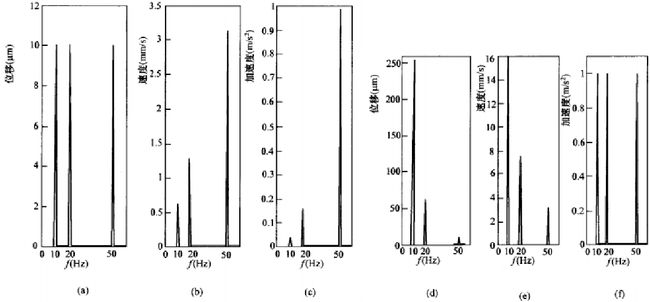
假设某故障振动位移信号频谱如图所示,频谱中10Hz、20Hz和50Hz分量幅值都为10μm。根据式(1-3)计算出每一频率分量的速度和加速度幅值,从而得到相应的振动速度和加速度频谱,如图(b)、©所示。比较这三个图可见,高频分量在振动速度和加速度频谱中得到了明显“放大”,频率越高,速度和加速度频谱中高频分量的“放大”作用越明显。因此对于高频振动故障,为了在故障的早期能够比较明显地反映出振动变化,采用振动速度或加速度监测比较有效。
表总结了振动位移、速度和加速度之间的关系:
| 振动表示形式 | 幅值 | 相位 | 频率 | 单位 |
|---|---|---|---|---|
| 位移 | A A A | φ \varphi φ | f f f | mm |
| 速度 | ω A \omega A ωA | φ + π 2 \varphi + \frac{\pi}{2} φ+2π | f f f | mm/s |
| 加速度 | ω 2 A \omega^2 A ω2A | φ + π \varphi + \pi φ+π | f f f | mm/s² |
转换关系
-
从位移到速度和加速度:
- 位移对时间求导得到速度: v = d y d t = ω A cos ( ω t + φ ) v = \frac{dy}{dt} = \omega A \cos(\omega t + \varphi) v=dtdy=ωAcos(ωt+φ)
- 速度对时间求导得到加速度: a = d v d t = − ω 2 A sin ( ω t + φ ) a = \frac{dv}{dt} = -\omega^2 A \sin(\omega t + \varphi) a=dtdv=−ω2Asin(ωt+φ)
-
从加速度到速度和位移:
- 加速度对时间积分得到速度: v = ∫ a d t v = \int a \, dt v=∫adt
- 速度对时间积分得到位移: y = ∫ v d t y = \int v \, dt y=∫vdt
选用原则
- 三种表示方式都可以用于监测。
- 速度和加速度信号更能突出反映高频分量的变化:
- 高频振动在速度和加速度频谱中会被“放大”,频率越高,这种“放大”作用越明显。
- 位移信号更能突出反映低频分量的变化:
- 低频振动在位移频谱中会被“放大”,频率越低,放大效果越明显。
简单振动问题分析
一、无阻尼自由振动分析
考虑一个由质量块、阻尼器和弹簧组成的简单振动模型(如图1-9所示)。当不考虑阻尼力和外界干扰力时,系统的运动方程为:
y ′ ′ + ω n 2 y = 0 y'' + \omega_n^2 y = 0 y′′+ωn2y=0
其中, ω n = k m \omega_n = \sqrt{\frac{k}{m}} ωn=mk 为系统固有频率。解为:
y = A sin ( ω n t + φ ) y = A \sin(\omega_n t + \varphi) y=Asin(ωnt+φ)
自由振动频率 ω n \omega_n ωn 与外界因素无关,只取决于系统本身的质量和刚度。工程上常通过调整系统刚度或质量来改变固有频率,以避开共振区。
二、有阻尼系统自由振动分析
有阻尼系统的自由振动方程为:
y ′ ′ + 2 ξ ω n y ′ + ω n 2 y = 0 y'' + 2 \xi \omega_n y' + \omega_n^2 y = 0 y′′+2ξωny′+ωn2y=0
其解为:
y = A e − ξ ω n t sin ( ω d t + φ ) y = A e^{-\xi \omega_n t} \sin(\omega_d t + \varphi) y=Ae−ξωntsin(ωdt+φ)
其中, ω d = ω n 1 − ξ 2 \omega_d = \omega_n \sqrt{1 - \xi^2} ωd=ωn1−ξ2 为有阻尼自由振动频率。振动解的性质取决于阻尼系数 ξ \xi ξ:
- 当 ξ ≥ 1 \xi \geq 1 ξ≥1 时,系统为强阻尼状态,振动呈指数衰减。
- 当 ξ < 1 \xi < 1 ξ<1 时,系统为弱阻尼状态,振动呈振荡衰减。
振动传感器
振动传感器的基本功能是将振动信号转换为电信号。常用的振动传感器有电涡流型、速度型和加速度型。
电涡流传感器
电涡流传感器通过高频电磁场和金属导体之间的电涡流效应来测量振动位移。其输出电压与感应线圈和金属导体之间的距离成正比。电涡流传感器的特点包括:
- 非接触测量,适用于转动部件的振动测量。
- 可测量转速和相位。
- 输出结果与被测物体材料有关,需重新标定。
- 安装要求严格,需避免高温、交叉感应、头部侧隙过小等问题。
速度传感器
速度传感器实际上是一个往复式永磁小发电机。其输出电压正比于振动速度。速度传感器的特点包括:
- 安装简单,可采用手扶方式或通过磁座固定。
- 体积和质量较大,低频特性较差,测量10Hz以下振动时需补偿。
- 可能受到电磁干扰,特别是在测量发电机和励磁机振动时。
加速度传感器
加速度传感器利用压电材料的压电特性,输出电荷与振动加速度成正比。其特点包括:
- 体积小、质量轻,适用于细小和质量较轻部件的振动测试。
- 结构紧凑,不易损坏。
传感器选用原则
- 电涡流传感器:适用于测量转轴振动,突出反映低频分量变化。
- 速度传感器:适用于测量轴承座振动,突出反映低频分量变化。
- 加速度传感器:适用于测量高频分量或脉冲量变化。
旋转机械振动标准
振动直接影响大型旋转机械的安全和稳定运行。常见的振动评定尺度包括轴承座振动位移、轴承座振动烈度和轴振动位移。
轴承座振动
轴承座振动以轴承座垂直、水平和轴向三个方向中的最大振动为评定依据。主要监测尺度包括:
- 轴承座振动位移:以振动位移信号的峰峰值为尺度。我国《电力工业技术管理法规》中规定的汽轮发电机组轴承振动位移标准如下表所示:
| 转速 (r/min) | 优 (μm) | 良 (μm) | 合格 (μm) |
|---|---|---|---|
| 1500 | 70 | 50 | 30 |
| 3000 | 30 | 20 | 10 |
- 轴承振动烈度:振动速度幅值同时反映了振动位移幅值和频率的影响。振动烈度监测通常采用振动速度的均方根值(单位为mm/s)。振动速度有效值与振动位移峰峰值之间的关系为:
v m = 0.707 × 1 0 − 3 × ω A pp v_m = 0.707 \times 10^{-3} \times \omega A_{\text{pp}} vm=0.707×10−3×ωApp
对于频率为50Hz的振动, v m = 0.11 A pp v_m = 0.11 A_{\text{pp}} vm=0.11App。
我国参照国际标准化组织ISO 10816-2:1996制定了大型旋转机械振动烈度评价标准,将振动评价区域分为四个区:
| 区域 | 定义 |
|---|---|
| 区域A | 新投产机组的振动应在此区域内 |
| 区域B | 振动在此区域内的机组通常认为是合格的,可以长期运行 |
| 区域C | 振动在此区域内的机组不适宜长期连续运行 |
| 区域D | 振动在此区域内,通常认为其剧烈程度足以引起机组破坏 |
转轴振动标准
轴承座振动不能完全反映转轴在轴瓦内的振动。轴振动有相对振动和绝对振动两种测量方式。国际标准化组织ISO 7919-2:1996制订的《陆地安装大型汽轮发电机组旋转轴径向振动测量与评价标准》适用于陆地安装、功率大于50MW、额定转速范围从1500~3600r/min的电站大型汽轮发电机组。轴振动测量参数是通频振动峰峰值,以在两个相互垂直方向上测得的位移峰峰值中较大者作为评定依据。
表1-9和表1-10分别给出了大型汽轮发电机组轴相对振动和绝对振动的标准:
| 额定转速 (r/min) | 区域A/区域B (μm) | 区域B/区域C (μm) | 区域C/区域D (μm) |
|---|---|---|---|
| 3000或3600 | 75/90 | 150/185 | 240/290 |
| 1500或1800 | 80/100 | 165/200 | 260/320 |
表1-11给出了GB/T 11348.2—1997《旋转机械转轴径向振动的测量和评定 第2部分:陆地安装的大型汽轮发电机组》制定的50MW以上汽轮发电机组轴振动标准:
| 区域 | 相对振动 (μm) | 绝对振动 (μm) |
|---|---|---|
| 区域A | 80 | 100 |
| 区域B | 120~165 | 150~200 |
| 区域C | 180~260 | 250~320 |
| 区域D | - | - |
表1-12给出了美国GE公司推荐的汽轮发电机组轴振标准:
| 额定转速 (r/min) | 良好 (μm) | 警报 (μm) |
|---|---|---|
| 125以上 | 25以下 | - |
对于额定转速从1000~30000r/min具有滑动轴承的耦合工业机器,我国标准GB/T 11348.3《旋转机械转轴径向振动的测量和评定 第3部分:耦合的工业机器》给出了振动标准区域:
| 区域边界 | A/B (μm) | B/C (μm) | C/D (μm) |
|---|---|---|---|
| 公式 | S p = 4800 / n S_p = 4800 / \sqrt{n} Sp=4800/n | S p = 9000 / n S_p = 9000 / \sqrt{n} Sp=9000/n | S p = 13200 / n S_p = 13200 / \sqrt{n} Sp=13200/n |
其中, n n n 为旋转速度,单位为r/min。