【强化学习的数学理论:了解强化学习名词脉络】
学习笔记:了解强化学习名词脉络
- 导论
-
- 分类
- Chapter 1. Basic Concepts
- Chapter 2. Bellman Equation
-
-
- One concept. state value
- One tool. Bellman Equation
- 策略评价 Policy evalution
-
- Chapter 3. Bellman Optimality Equation 贝尔曼最优公式
-
-
- A special Bellman equation
- Two concepts:
- One tool:
- Optimality
-
- Chapter 4 . Value Iteration & Policy Iteration
-
-
- First algorithms for optimal policies
- Three algorithms
- Policy update and value update
- Need the environment model
-
- Chapter 5 . Monte Carlo Learning
-
-
- Gap:how to do model-free learning
- Mean estimation with sampling data
-
- First model-free RL algorithms
- Alogrithms
-
- Chapter 6 . Stochastic Approximation 随机近似理论
-
-
- Gap: from non-incremental to incremental
- Mean estimation
- Algorithms:三种算法
- Incremental manner and SGD
-
- Chapter 7 . Temporal-Difference Learning 时序差分方法
-
-
- Gap:Classic RL algorithms
- Algorithms:
-
- Chapter 8 . Value Function Approximation
-
-
- Gap:tabular representation to function representation
- Algorithms:
- Neutral networks come into RL
-
- Chapter 9 . Policy Gradient Methods
-
-
- Gap:from value-based to policy-based
- Contents:
-
- Chapter 10 . Actor-Critic Methods
-
-
- Gap: value-based + policy-based
- Algorithms:
-
B站听课笔记:
对强化学习原理的基本了解,后续将深入学习。
导论
学习强化学习的目标:一个是原理部分,另一是实践和编程部分。
原理部分花费大量时间——数学性强,系统性强
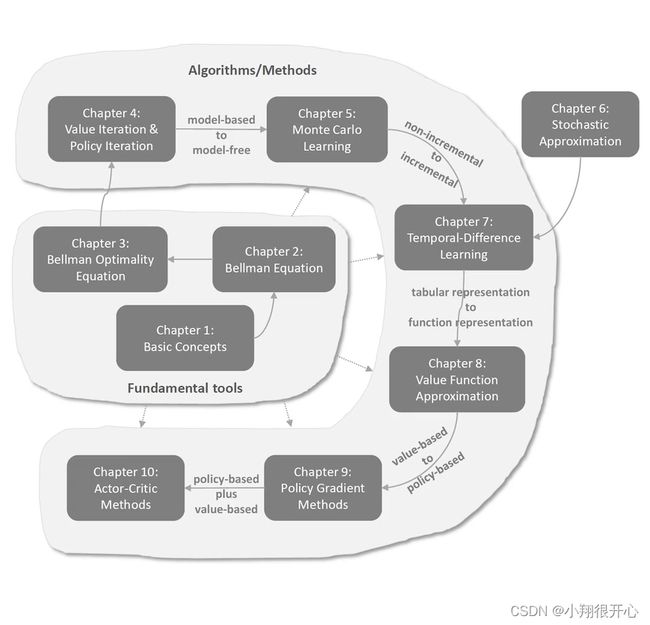
分类
- Fundamental tools 基础工具板块
- Algorithms/Methods数学算法和方法板块
Chapter 1. Basic Concepts
- Concepts:1. state 2. action 3. reward 4. return 5. episode 6. policy
- Grid-world examples 网格例子
- Markov decision process (MDP框架)
- Fundamental concepts,widely and later
Chapter 2. Bellman Equation
One concept. state value
状态值——从一个状态出发,沿着一个策略,所得到奖励回报的平均值。
v π ( z ) = E [ G t ∣ S t = s ] . \ v_\pi (z) = \ E[ \ G_t | \ S_t = s]. vπ(z)= E[ Gt∣ St=s].
状态值越高,说明对应的策略越好;状态值越低,说明沿着该策略得到的奖励是较少的。
状态值能去评价一个策略的好坏
One tool. Bellman Equation
分析状态值的工具——描述所有状态,状态值之间的关系
v π = r π + γ P π v π \ v_\pi = r_\pi + \gamma P_\pi v_ \pi vπ=rπ+γPπvπ
策略评价 Policy evalution
widely used later
Chapter 3. Bellman Optimality Equation 贝尔曼最优公式
强化学习的最终目的:求解最优策略
A special Bellman equation
Two concepts:
- optimal policy π ∗ \ {\pi} ^* π∗ 最优策略
- optimal state value
One tool:
Bellman optimality equation: v = m a x π ( γ P π v ) = f ( v ) \ v = \ max_{\pi} (\gamma P_\pi v) = f(v) v= maxπ(γPπv)=f(v)
1、不动点原理 fixed-point theorem——解释了两个方面
2、fundamental problems 基础性的问题,一定有解。
3、an algorithm solving the equation
Optimality
widely used later
Chapter 4 . Value Iteration & Policy Iteration
First algorithms for optimal policies
首要的最优策略算法
Three algorithms
value iteration 值迭代 ——第三章的bellman最优策略公式的迭代表达
policy iteration 策略迭代——第五章应用
truncated policy iteration 值迭代和策略迭代的统一方式
Policy update and value update
迭代算法中的两个子步骤:Policy update 和 value update,widely used later
两个步骤不断迭代,从而得到最优策略。
Need the environment model
需要模型
Chapter 5 . Monte Carlo Learning
Gap:how to do model-free learning
没有模型的情况,可以用蒙托卡罗强化学习算法。
Mean estimation with sampling data
E [ X ] ≈ x ˉ = 1 n ∑ i = 1 n x i E[X] ≈ \bar{x} = \frac {1}{n} \sum _{i=1}^{n} x_i E[X]≈xˉ=n1i=1∑nxi
随机变量的期望值E[X]
First model-free RL algorithms
Alogrithms
1、MC basic——将第四章中policy iteration中的依赖于模型的那部分更换为依赖于数据的。
实际情况不能用,效率非常低
2、MC exploring starts
3、MC ϵ \epsilon ϵ-greedy
Chapter 6 . Stochastic Approximation 随机近似理论
Gap: from non-incremental to incremental
过渡章节,从非增量到增量
Mean estimation
估计一个随机变量的期望值E[X],两种方法:
non-incremental——将所有采样全部采到后,一次性求平均,得到E[X]的近似。
incremental——开始有估计值,得到一个采样后,对估计值更新一次,从而使得估计值越来越准。在样本采样的过程中,就可以用该值了,虽然该值可能不太准确。
Algorithms:三种算法
1、Robbins-Monro (RM) algorithm——实际上是在求解一个函数等于0的方程。
即RM算法是为了求解 ω \omega ω 取什么值时, G ( ω ) = 0 G(\omega) =0 G(ω)=0成立。
RM算法不需要知道函数表达式、梯度、导数等均不需要知道就可以求出来。
2、Stochastic gradient descent (SGD)——随机梯度下降,一种特殊的RM算法。
3、SGD,BGD,MBGD的比较
BGD:batch gradient descent
MBGD:mini-batch gradient descent
Incremental manner and SGD
增量式算法的思想和SGD的思想,widely used later
Chapter 7 . Temporal-Difference Learning 时序差分方法
Gap:Classic RL algorithms
一种非常经典的方法
Algorithms:
1、TD learning of state values
利用TD的方法来学习state values,能比较好地揭示TD方法地思想是什么。
chapter5利用蒙托卡罗的方法来计算state value,chapter4利用模型来计算state value,本章利用时序差分的方法来计算state value。
2、Sarsa: TD learning of action values
利用TD的思想来学习action value,并以此为依据去更新策略,得到一个新的策略再得到一个新的action value,这样不断循环下去就能不断地去改进策略,直到最后得到一个最优的策略。
3、Q-learning:TD learning of optimal action values
直接计算 optimal action values,是一个 off-policy算法。
- on-policy & off-policy
- 强化学习中有两个策略:
一个是behavior policy,用来生成经验数据;
另一个是target policy,这是目标策略,我们不断改进来希望target policy能够收敛到最优策略。
如果behavior policy和target policy相同,那么它就是on-policy,如果不同,则是off-policy。 - off-policy的好处——可以用之前别的策略生成的数据为我所用,拿去学习然后得到最优策略
4、Unified point of view
统一化视角——很多算法,实际上它的表达式非常类似,其求解的数学问题也非常类似。
Chapter 8 . Value Function Approximation
Gap:tabular representation to function representation
第七章及以前部分,全都是基于表格形式的。
即:每一个状态都对应一个状态值 v π ( s ) v_\pi (s) vπ(s),这些状态值存在一个表格或向量中。访问和修改都非常容易。
但是,当状态非常多或者状态是连续的,这种表格形式的效率比较低下或不再适用了。这时候用函数的形式去代替。
即函数 v ^ ( s , ω ) \hat{v}(s,\omega) v^(s,ω)能够和真实的 v π ( s ) v_\pi (s) vπ(s)越接近越好。
Algorithms:
1、State value estimation with value function approximation (VFA):
m i n ω J ( ω ) = E [ v π ( S ) − v ^ ( S , ω ) ] min_{\omega} J(\omega) = E[v_\pi (S)- \hat v(S,\omega)] minωJ(ω)=E[vπ(S)−v^(S,ω)]利用VFA思想去来做state value estimation。
- 如何去做?
1)明确一个目标函数;
2)求目标函数的梯度;
3)用梯度上升或梯度下降对目标函数进行优化。
2、Sarsa with VFA
VFA思想与Sarsa相结合,来估计action value,再和policy improvement相结合,不断迭代来得到最优策略。
3、Q-learning with VFA
VFA思想与Q-learning相结合,来估计action value,再和policy improvement相结合,不断迭代来得到最优策略。
4、Deep Q-learning
DQN里面有很多技术,比如:用两个网络或者经验回放等
Neutral networks come into RL
神经网络是函数非常好的一个表达方式,本章中,神经网络首次进入强化学习中。
Chapter 9 . Policy Gradient Methods
Gap:from value-based to policy-based
第九章、第十章都是policy-based的方法。
- value-based 和policy-based的区别?
-value-based的方法: J ( ω ) J(\omega) J(ω)中的 ω \omega ω是值函数的参数,更新 ω \omega ω使得值函数能更好地近似或估计出一个策略所对应的值,在此基础之上更新策略,依此重复然后不断找到最优的策略。
-policy-based的方法:目标函数 J ( θ ) J(\theta) J(θ)的策略参数 θ \theta θ。此方法将策略从表格形式变成了函数形式。即:直接去优化 θ \theta θ(直接改变策略),慢慢地就得到最优的策略。
Contents:
1、Metrics to define optimal policies:
J ( θ ) = v ˉ π + r ˉ π J(\theta) = \bar v_\pi + \bar r_\pi J(θ)=vˉπ+rˉπ
1)明确目标函数 v ˉ π 和 r ˉ π \bar v_\pi 和 \bar r_\pi vˉπ和rˉπ;
2)求目标函数的梯度;
3)用梯度上升或梯度下降对目标函数进行优化。
2、Policy gradient:目标函数所对应的梯度Policy gradient
∇ J ( ω ) = E [ ∇ θ l n π ( A ∣ S , θ ) q π ( S , A ) ] \nabla J(\omega) = E[\nabla_\theta ln \pi(A| S,\theta) q_\pi(S,A)] ∇J(ω)=E[∇θlnπ(A∣S,θ)qπ(S,A)]
著名的Policy gradient定理。该定理直接给出来它的梯度。
相对来说求该梯度是一个比较复杂的过程。仅熟悉该表达式即可。
3、Gradient-ascent algorithms (REINFORCE)
θ t + 1 = θ t + α ∇ θ l n π ( a t ∣ s t , θ t ) q t ( s t , a t ) \theta _{t+1} = \theta _{t} + \alpha \nabla_\theta ln \pi(a_t| s_t,\theta _t) q_t(s_t,a_t) θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)
当有了梯度,就可来做梯度上升,去最大化目标函数。此时可用到一个非常经典的Policy gradient的方法——REINFORCE
Chapter 10 . Actor-Critic Methods
Gap: value-based + policy-based
将第九章和第八章的内容结合在一起。本章的actor-critic方法就是第九章的policy gradient方法。
为了突出value所起到的作用。其中的actor对应的是policy update,critic对应的是value。
- 如何理解 Actor-Critic的架构?
利用下式可以表达该架构:
θ t + 1 = θ t + α ∇ θ l n π ( a t ∣ s t , θ t ) q t ( s t , a t ) \theta _{t+1} = \theta _{t} + \alpha \nabla_\theta ln \pi(a_t| s_t,\theta _t) q_t(s_t,a_t) θt+1=θt+α∇θlnπ(at∣st,θt)qt(st,at)
Algorithms:
1)The simplest actor-critic (QAC)
即为上式。
-
Advantage actor-critic (A2C)
引入一个baseline来减小估计的方差。 -
Off-policy actor-critic
actor-critic本质上还是policy gradient,policy gradient自然的是一种on-policy的算法。可以用importance sampling(重要性采样)来变成Off-policy的算法。
所有的on-policy都可以用重要性采样来变成off-policy
以上三种方法都要求策略是随机的,也就是在每个状态,都能概率选择到所有的action
- Deterministic actor-critic (DPG)
也可以用到确定性的策略deterministic
用数学语言去描述一个问题,是最高效的一种方法。