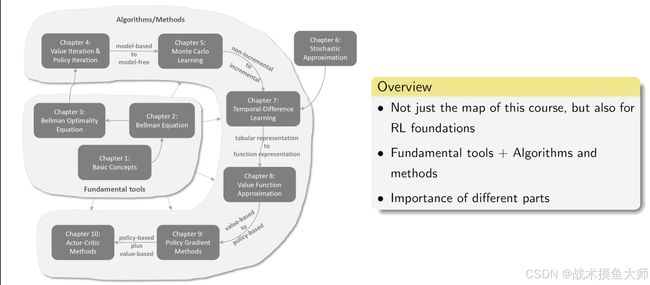
强化学习原理：基本概念

脉络图

图片来自西湖大学赵世钰老师课程截图

理论基础

Basic Concepts

被训练的目标被称为agent，agent的所有可能的状态组合形成状态空间$S=\left\{s_i\right\}$，处于每个状态时所能执行的行动称为action，每个状态对应的action构成一个action space：$A(s_i)=\left\{a_i\right\}$，从一个状态经过一个action到达另一个状态，称为状态转移$s_1\stackrel{a_2}{\to }{s}_2$，

感觉有点像有限状态机模型

对于行为具有固定结果状态的情况，可以将action和state列出来，形成一个表格：

	$a_1$	$a_2$
$s_1$	$s_1$	$s_2$
$s_2$	$s_2$	$s_1$

更一般化，可以以概率的形式表达$p(s_2|s_1,a_2)=0.5,p(s_1|s_1,a_2)=0.5$
每个状态下的决策系统被称为policy策略，用$\pi$表示，$\pi (a_1|s_1)$表示在该策略指导下，在$s_1$状态下执行$a_1$的概率是多少，同一状态下所有action和应该为1，策略也可以用表格表示

	$a_1$	$a_2$
$s_1$	$0.6$	$0.4$
$s_2$	$0.6$	$0.5$

Reward：每次action之后，得到一个score，表示对该行为的鼓励or惩罚，可以通过设计reward来实现对RL的控制，reward的设计可以用表格来表示。

	$a_1$	$a_2$
$s_1$	$r_1$	$r_2$
$s_2$	$r_3$	$r_4$

也可以用概率表示，p(r1 | s_1,a_1)表示在$s_1$状态下，$a_1$行为得到$r_1$ reward的概率，所有可能的reward概率和应该为1。

trajectory is a state-action-reward chain，也就是agent不断作出动作的轨迹：$s_1\stackrel{a_2}{\to }{s}_2\stackrel{a_2}{\to }{s}_1$
return是指一个trajectory所有action的reward的和$return=r1+r2$，用于评价trajectory或policy的优劣。为了控制轨迹过长的情况，引入discount rate $\gamma$，$discountedreturn=r1+{\gamma }^1{r}_2+{\gamma }^{2}r3+...$ ，通过调节discount rate可以调节策略的偏好

当agent进入来terminal states，停止运行，形成的trajectory称为episode

terminal states就是目标状态，到达这个状态就停止，很多任务是没有terminal states，episode任务和continus任务是可以互相转换的，例如把目标状态的action space设定为只有一个action就是停在原地，episode任务就变成了continus任务。

markov decesion process(MDP)

• 集合
  • 状态空间，行为空间，奖励空间
• 概率分布：
  • 行为结果状态概率，行为reward概率
• 策略模型
• 马尔可夫性：当下概率仅与上一状态有关，与更前面的状态无关

如果策略一旦确定，概率融入到模型里了，就不需要策略模型了，MDP就变成了MP马尔可夫模型

Bellman Equation贝尔曼公式

state value

return的计算方式：

• 定义法，按照轨迹中的每个action的return加和
• 递归求return，从该state出发的轨迹的return依赖于该步本身的$r$以及后续state出发的轨迹的return，可以得出方程$v1=r_1+\gamma v2$，每个state的列一下方程，就可以得到一个线性方程组，解线性方程组可得return值。
  • v1,v2表示从$s_1{s}_2$出发的所有轨迹的return的平均值(期望)
  • 在RL中被称为bootstrapping，

对于策略而言，将整个轨迹以更一般的形式写出来：
$$S_t\stackrel{A_t}{}{R}_{t+1},S_{t+1}\stackrel{A_{t+1}}{}{R}_{t+2},S_{t+2}\stackrel{A_{t+2}}{}{R}_{t+3},\dots$$
其中所有的大写符号都是随机变量，discounted return计算如下：
$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\dots$$
为了评价策略，定义state value为一个策略所可能出现的所有轨迹的discounted return $G_t$的期望值$v_{\pi }=E[G_t|S_t=s]$,是一个关于初始状态s的函数，代表了该state的value，如果一个state的value高，表示该state更有价值，值得我们向这个state前进。

Bellman equation贝尔曼公式

结合上面的递推公式以及 discounted return公式，得到$G_t=R_{t+1}+G_{t+1}$，因此:
$$E(G_t|S_t=s)=E(R_{t+1}+G_{t+1}|S_t=s)=E(R_{t+1}|S_t=s)+E(G_{t+1}|S_t=s)$$
其中：
$$\begin{array}{rl}E(R_{t+1}|S_t=s)& =\sum _a\pi (a|s)E[R_{t+1}|S_t=s,A_t=a]\\ & =\sum _a\pi (a|s)\sum _{r}p(r|s,a)r\end{array}$$
表示从s出发，进行一次action的平均reward
$$\begin{array}{rl}\mathbb{E}[G_{t+1}|S_t=s]& \begin{array}{r}=\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_t=s,S_{t+1}=s^{\prime }]p(s^{\prime }|s)\end{array}\\ & =\sum _{s^{\prime }}\mathbb{E}[G_{t+1}|S_{t+1}=s^{\prime }]p(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })p(s^{\prime }|s)\\ & =\sum _{s^{\prime }}{v}_{\pi }(s^{\prime })\sum _{a}p(s^{\prime }|s,a)\pi (a|s)\end{array}$$
表示从s出发，到达的下一状态的state value的平均值。
得到Bellman equation：
$$\begin{array}{rl}{v}_{\pi }(s)& =\mathbb{E}\left[R_{t+1}\mid S_t=s\right]+\gamma \mathbb{E}\left[G_{t+1}\mid S_t=s\right],\\ & =\underset{\text{mean of immediate rewards }}{\sum _a\pi (a\mid s)\sum _{r}p(r\mid s,a)r}+\underset{\text{mean of future rewards }}{\gamma \sum _a\pi (a\mid s)\sum _{s^{\prime }}p\left(s^{\prime }\mid s,a\right)v_{\pi }\left(s^{\prime }\right)},\\ & =\sum _a\pi (a\mid s)\left[\sum _{r}p(r\mid s,a)r+\gamma \sum _{s^{\prime }}p\left(s^{\prime }\mid s,a\right)v_{\pi }\left(s^{\prime }\right)\right],\forall s\in \mathcal{S}.\end{array}$$
看整理后的bellman公式，就是每个轨迹的discounted return乘以policy得出执行每个action的概率。
所以可以用于评估策略模型。
将前者定义为$r_{\pi }(s_i)$，表示前者执行action的return的期望值，后者定义为$p_{\pi }(s_j|s_i)={\sum }_{a}p(s^{\prime }|s,a)\pi (a|s)$表示从$s_i$到$s_j$的概率，可以简写为：
$$\begin{gathered} v_{\pi }(s)=r_{\pi }(s)+\gamma \sum _{s^{\prime }}{p}_{\pi }(s^{\prime }|s)v_{\pi }(s^{\prime })\text{(1)} \\ {r}_{\pi }(s)\triangleq \sum _a\pi (a|s)\sum _{r}p(r|s,a)r,p_{\pi }(s^{\prime }|s)\triangleq \sum _a\pi (a|s)p(s^{\prime }|s,a) \end{gathered}$$
考虑所有state列方程，可以得到矩阵形式的贝尔曼方程：
$$v_{\pi }=r_{\pi }+\gamma P_{\pi }{v}_{\pi }$$

where

$\bullet$ $v_{\pi }=[v_{\pi }(s_1),\dots ,v_{\pi }(s_n){]}^T\in {\mathbb{R}}^n$

$\bullet$ $r_{\pi }=[r_{\pi }(s_1),\dots ,r_{\pi }(s_n){]}^T\in {\mathbb{R}}^n$

$\bullet$ $P_{\pi }\in {\mathbb{R}}^{n\times n}$, where $[P_{\pi }{]}_{ij}=p_{\pi }(s_j|s_i)$, is the state transition matrix
例子如下：
[ v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) ] = [ r π ( s 1 ) r π ( s 2 ) r π ( s 3 ) r π ( s 4 ) ] ⏟ r π + γ [ p π ( s 1 ∣ s 1 ) p π ( s 2 ∣ s 1 ) p π ( s 3 ∣ s 1 ) p π ( s 4 ∣ s 1 ) p π ( s 1 ∣ s 2 ) p π ( s 2 ∣ s 2 ) p π ( s 3 ∣ s 2 ) p π ( s 4 ∣ s 2 ) p π ( s 1 ∣ s 3 ) p π ( s 2 ∣ s 3 ) p π ( s 3 ∣ s 3 ) p π ( s 4 ∣ s 3 ) p π ( s 1 ∣ s 4 ) p π ( s 2 ∣ s 4 ) p π ( s 3 ∣ s 4 ) p π ( s 4 ∣ s 4 ) ] ⏟ P π [ v π ( s 1 ) v π ( s 2 ) v π ( s 3 ) v π ( s 4 ) ] ⏟ v π . \left.\left[\begin{array}{c}v_\pi(s_1)\\v_\pi(s_2)\\v_\pi(s_3)\\v_\pi(s_4)\end{array}\right.\right]=\underbrace{\left[\begin{array}{c}r_\pi(s_1)\\r_\pi(s_2)\\r_\pi(s_3)\\r_\pi(s_4)\end{array}\right]}_{r_\pi}+\gamma\underbrace{\left[\begin{array}{c}p_\pi(s_1|s_1)&p_\pi(s_2|s_1)&p_\pi(s_3|s_1)&p_\pi(s_4|s_1)\\p_\pi(s_1|s_2)&p_\pi(s_2|s_2)&p_\pi(s_3|s_2)&p_\pi(s_4|s_2)\\p_\pi(s_1|s_3)&p_\pi(s_2|s_3)&p_\pi(s_3|s_3)&p_\pi(s_4|s_3)\\p_\pi(s_1|s_4)&p_\pi(s_2|s_4)&p_\pi(s_3|s_4)&p_\pi(s_4|s_4)\end{array}\right]}_{P_\pi}\underbrace{\left[\begin{array}{c}v_\pi(s_1)\\v_\pi(s_2)\\v_\pi(s_3)\\v_\pi(s_4)\end{array}\right]}_{v_\pi}. ​vπ​(s1​)vπ​(s2​)vπ​(s3​)vπ​(s4​)​ ​=rπ​ ​rπ​(s1​)rπ​(s2​)rπ​(s3​)rπ​(s4​)​ ​​​+γPπ​ ​pπ​(s1​∣s1​)pπ​(s1​∣s2​)pπ​(s1​∣s3​)pπ​(s1​∣s4​)​pπ​(s2​∣s1​)pπ​(s2​∣s2​)pπ​(s2​∣s3​)pπ​(s2​∣s4​)​pπ​(s3​∣s1​)pπ​(s3​∣s2​)pπ​(s3​∣s3​)pπ​(s3​∣s4​)​pπ​(s4​∣s1​)pπ​(s4​∣s2​)pπ​(s4​∣s3​)pπ​(s4​∣s4​)​ ​​​vπ​ ​vπ​(s1​)vπ​(s2​)vπ​(s3​)vπ​(s4​)​ ​​​.

$P_{\pi }就是概率论里面马尔可夫链中的状态转移矩阵$

使用矩阵形式的Bellman公式求state value时，一般都是使用叠代法求解，先估计一个结果$v_0$，带入$v_{k+1}=r_{\pi }+\gamma P_{\pi }{v}_k$，随着k的增大，$v_k$收敛于$v_{\pi }$

这里收敛的原因，跟现代控制工程中的观测器收敛是一样的原因，观测值和实际值间的error是不断趋于0的。

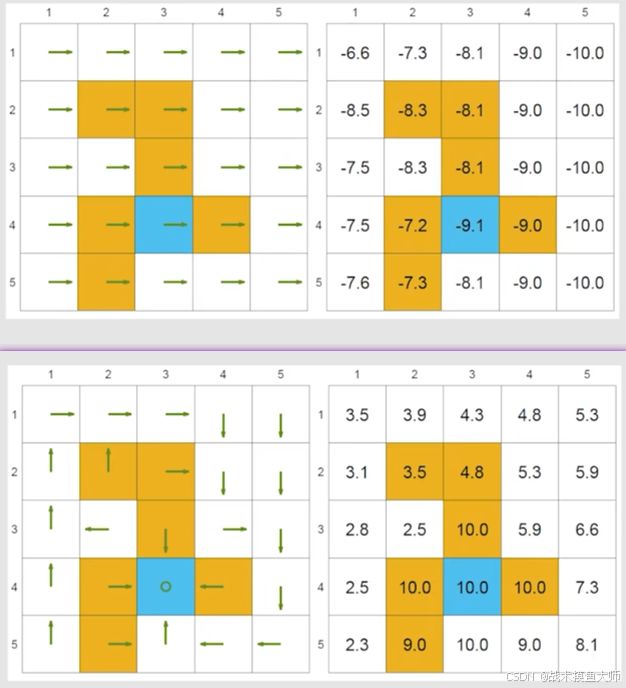
这个图是赵老师PPT里面的图，上面是一个较差策略的结果，下面是较好策略的结果。

action value

action value表示该action的价值，policy依据action value判断选择哪个action执行。action value定义如下：
$$q_{\pi }(s,a)=\mathbb{E}[G_t|S_t=s,A_t=a]$$
含义是从s状态出发，选择a行为时的discounted return

只是帮助理解，严格来说，这个不是discounted return，因为它只限定了第一个action，并不是一个路径

action value和state value的联系：
$$\begin{gathered} \underset{v_{\pi }(s)}{\mathbb{E}[G_t|S_t=s]}=\sum _a\underset{q_{\pi }(s,a)}{\mathbb{E}[G_t|S_t=s,A_t=a]}\pi (a|s) \\ {v}_{\pi }(s)=\sum _a\pi (a|s)q_{\pi }(s,a) \end{gathered}$$

可以参考上面的贝尔曼公式得到action value的计算公式$q_{\pi }(s,a)=r_a+\gamma v_{\pi }{s}_j$

Bellman Optimality Equation 贝尔曼最优公式

最优策略

如果有两个策略${\pi }_1$和${\pi }_2$,如果满足$v_{{\pi }_1}(s)\ge v_{{\pi }_2}(s),\forall s\in S$，则称${\pi }_1$优于${\pi }_2$，如果一个策略比任意策略都优，就称为最优策略。

存在性，唯一性，确定性，都可以通过贝尔曼最优公式证明

贝尔曼最优公式

element-wise form：
$$\begin{array}{rl}v(s)& =\underset{\pi }{\max }\sum _a\pi (a\mid s)\left(\sum _{r}p(r\mid s,a)r+\gamma \sum _{s^{\prime }}p\left(s^{\prime }\mid s,a\right)v\left(s^{\prime }\right)\right),\forall s\in \mathcal{S}\\ & =\underset{\pi }{\max }\sum _a\pi (a|s)q(s,a)\end{array}$$
matrix from：
$$v=\underset{\pi }{\max }(r_{\pi }+\gamma P_{\pi }v)$$

$\gamma$的取值会影响策略对远近reward的取舍，$\gamma$越大越远视，越小越近视，如果设为0，策略就只会考虑第一步的reward
如果reward奖励改为了$ar+b$，相应的state value改为$v^{\prime }=av+\frac{b}{1-\gamma }1$，action value也会一样变化。

求解最优策略

根据action value更新策略，将action value较大的action的概率调高/直接设置为1。
流程如下：

• 初始化策略${\pi }_0$和state value向量 $v_0$
• 带入贝尔曼最优化公式，求解出$v_1$
• 根据$v_1$求解出action value
• 根据action value更新策略${\pi }_1$
• 根据${\pi }_1$和$v_1$计算$v_2$
• …

每次都选择action value最大的action，一定会得到最优策略

证明：

前置知识：contraction mapping theorem

不动点fixed point：$f(x)=x$
收缩映射contraction mapping：$||f(x_1)-f(x_2)||\le \gamma ||x_1-x_2||,\gamma \in (0,1)$
这些都是可以扩展到向量和矩阵的，相应的绝对值变为向量模

对于一个线性函数：$f(x)=ax$，可以得到0是一个不动点，当$ain(0,1)$时是一个contraction mapping
扩展到矩阵向量形式里面：$f(x)=Ax，x\in R^n,A\in R^{n\times n}$,可以得到0向量是一个不动点，当$||A||\le 1$的时候，是个contraction mapping
对于任意$f(x)=x$的等式，如果$f$是contraction mapping，那么：

• 一定存在fixed point
• fixed point一定是唯一的
• 可以通过$x_{k+1}=f(x_k)$的方式迭代求解

这不就是把这个问题当作控制问题来解决了嘛？如果A的特征值小于1，x收敛
至于该最优state value是否存在，看赵老师课程讲解

Ref

【【强化学习的数学原理】课程：从零开始到透彻理解（完结）