地图上的‘词向量’：揭秘 Space2Vec 的魔法

目前在调研处理地理位置坐标的方法，完善之前地理大模型的文章，现在调研一下这篇ICLR 2020的文章 Spece2Vec全名叫：MULTI-SCALE REPRESENTATION LEARNING FOR SPA- TIAL FEATURE DISTRIBUTIONS USING GRID CELLS。看看其中编码地图的思路或者方法能否有借鉴的地方。

论文地址：https://arxiv.org/pdf/2003.00824

代码地址：https://github.com/gengchenmai/space2vec

1. 背景

1.1 从NLP到空间世界

近年来（注意文章时间是2020年），自监督的文本编码模型在自然语言处理（NLP）中大放异彩。像 Word2Vec、GloVe、ELMo、BERT 这些模型，核心思路都是将“词语”转化为向量形式，这些向量不仅考虑词语本身，还融入了它在句子中的位置与上下文关系。这种向量化的表示方式极大提升了模型对语义的理解能力，并推动了 NLP 的飞跃式发展。

而在空间信息科学（GIScience）中，我们其实面临着非常类似的问题：一个地点的意义，往往不只取决于它的坐标位置，更依赖于它周围的空间环境。比如，一个 POI（Point of Interest）周围若都是餐厅，那它大概率也是商业相关的设施。因此，能否像处理文本一样，也为“空间中的每一个点”构建语义丰富的向量表示，就成为了空间人工智能迈向通用性的重要一步。

1.2 地理信息处理的问题

目前主流的空间表示方法，大多采取固定规则将地理坐标“离散化”，例如将城市划分成规则格子（tile embedding），或者将坐标直接喂入神经网络模型中。然而，这些方法在面对现实世界的多样空间分布时显得力不从心。不同类型的 POI 分布形式差异极大，例如女装店往往集中在商业区，而学校则分布均匀。若只用一个固定大小的网格对所有类型统一建模，不是会导致过拟合（格子太小），就是信息稀疏（格子太大）。

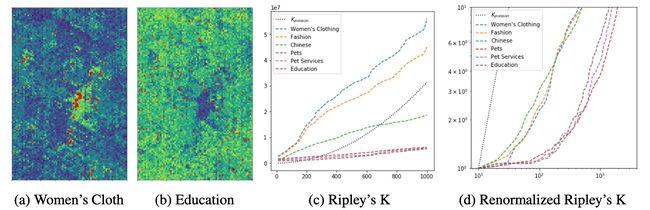
如下图所示，女装类 POI 在地图上呈现出高度聚集的分布，而教育类 POI 则分布更均匀。使用 Ripley’s K 方法分析可以发现，不同 POI 类型的密度增长曲线在不同尺度下变化明显。如果我们强行用相同尺度对它们建模，只会让模型性能在不同类型间失衡。因此，亟需一种支持“多尺度表达”的新方法，能同时适应局部聚集与大范围均匀的分布模式。

1.3 动机来源

值得一提的是，空间表示的“多尺度”问题，其实早已在生物学领域得到了回答。神经科学研究表明，哺乳动物的大脑中存在一种叫做“网格细胞（Grid Cells）”的神经元，它们以周期性的模式自动记录动物在空间中的位置。这种编码方式天然具有多尺度特性，帮助生物精准定位与路径导航。进一步研究发现，这种机制可以用多个角度相差 60° 的余弦函数叠加来模拟，构成一种六边形的周期性编码结构。

受到这一机制的启发，研究者提出了 Space2Vec 模型，通过引入多频率的正余弦函数，实现对地理位置的多尺度编码，并结合注意力机制来建模点与周围环境之间的空间关系。这个模型不仅在结构上模仿了大脑的导航系统，还在实际任务中展现出对不同空间分布的强适应性，为地理人工智能开辟了新的可能。

2. 问题设定

作者希望设计一个模型，能够对空间中的点进行“分布式表示”（Distributed Representation），即将地理空间中的每一个点表示成一个具有语义意义的向量。这种表示形式类似于自然语言处理中常见的词向量模型，但这里的“词”是地图上的“点”。

设一组空间点集合为：

$$\mathcal{P}=p_i$$

其中每个点 $p_i$ 表示一个 POI（Point of Interest），可以用位置和属性表示为：

$$p_i=({\mathbf{x}}_i,{\mathbf{v}}_i)$$

• ${\mathbf{x}}_i\in {\mathbb{R}}^L$：表示点的位置坐标（例如二维地图坐标 L=2）
• ${\mathbf{v}}_i$：表示与该点相关的属性信息，如 POI 类型、名称、容量等。

我们希望学习一个函数：

$$f_{\mathcal{P},\theta }(\mathbf{x}):{\mathbb{R}}^L\to {\mathbb{R}}^d$$

这个函数将任意坐标 $\mathbf{x}$ 映射为一个 d-维的向量表示，其中 $\theta$ 是模型的可训练参数。

这个函数的目标是捕捉空间中点的分布特性 $f_{\mathcal{P},\theta }(\mathbf{x})$，从而为任意位置生成有意义的向量表示。换句话说，这个表示不仅仅反映了点的几何位置，也蕴含了其语义背景。

在类比自然语言处理任务中：

• 词语的含义 = 词本身 + 它在句子中的位置；
• 地理空间中的点的含义 = 点的属性（如类型）+ 它在地图中的位置。

因此，属性 ${\mathbf{v}}_i$（例如“博物馆”）和坐标 ${\mathbf{x}}_i$ 就分别类比为 NLP 中的“词的种类”和“词的位置”，而我们要构建的就是一种适用于空间点的“空间向量模型”。

3. 方法

为了实现空间点特征的分布式表示（distributed representation of point-features in space），Space2Vec 采用了一个 编码器-解码器（encoder-decoder） 的框架。整个过程可以分为两个阶段：编码（Encoding）与解码（Decoding）。

首先，对于任意一个点 $p_i=({\mathbf{x}}_i,{\mathbf{v}}_i)$，其中 ${\mathbf{x}}_i$ 是该点的空间位置（如经纬度），${\mathbf{v}}_i$ 是其属性（例如 POI 类型、名称、容量等），将其分别进行编码：

• 位置编码器 $En{c}^{(x)}()$ 将位置 ${\mathbf{x}}_i$ 映射为一个向量 $\mathbf{e}[{\mathbf{x}}_i]\in {\mathbb{R}}^{d^{(x)}}$；
• 特征编码器 $En{c}^{(v)}()$ 将属性 ${\mathbf{v}}_i$ 编码为向量 $\mathbf{e}[{\mathbf{v}}_i]\in {\mathbb{R}}^{d^{(v)}}$。

最终，将两个向量拼接起来，形成该点的完整表示：

$${\mathbf{e}}_i=[\mathbf{e}[{\mathbf{x}}_i];\mathbf{e}[{\mathbf{v}}_i]]\in {\mathbb{R}}^d,\text{其中 }d=d^{(x)}+d^{(v)}$$

这里的 [ ; ] 表示向量拼接操作。如果某些点的属性信息未知（例如某些预测区域），我们也可以只使用位置编码 $\mathbf{e}[{\mathbf{x}}_j]$ 进行表示。

接下来，作者设计了两种解码器，用于从上述编码向量中“解读”出点的语义信息：

1. 位置解码器（Location Decoder）：记作 $De{c}_s()$，该解码器尝试仅通过位置向量 $\mathbf{e}[{\mathbf{x}}_i]$ 来重建或预测该点的特征向量 $\mathbf{e}[{\mathbf{v}}_i]$。这相当于“仅凭地理位置猜测它是什么”。
2. 空间上下文解码器（Spatial Context Decoder）：记作 $De{c}_c()$，该解码器使用目标点周围 $n$ 个邻居点的空间表示和特征信息 ${\mathbf{e}}_{i_1},\dots ,{\mathbf{e}}_{i_n}$ 来预测中心点的特征 $\mathbf{e}[{\mathbf{v}}_i]$。这更像是人类的推理方式：从“周围是什么”来判断“你可能是什么”。

通过这种编码-解码机制，Space2Vec 实现了对空间中任意点的多尺度建模，既可以独立理解位置本身，也能结合空间邻居构建更丰富的语义表达。

3.1 Encoder

3.1.1 Point Feature Encoder

Point Feature Encoder 的核心目标是：将空间中每个点所携带的属性信息（如 POI 类型、名称、功能等）编码为一个语义特征向量，记为 $\mathbf{e}[{\mathbf{v}}_i]\in {\mathbb{R}}^{d^{(v)}}$。这种向量可以作为模型输入的一部分，帮助模型理解不同点的“是什么”。

在实际实现中，如果一个地理点 $p_i$ 包含多个 POI 类型（这在现实中很常见，如“书店+咖啡厅”），我们会将这些类型各自的嵌入向量（embedding）取平均来获得该点的整体特征向量。具体公式如下：

$$\mathbf{e}[{\mathbf{v}}_i]=\frac{1}{H}\sum _{h=1}^H{\mathbf{t}}_h^{(\gamma )}$$

其中，$H$ 是该点拥有的 POI 类型数量，${\mathbf{t}}_h^{(\gamma )}$ 表示第 $h$ 个 POI 类型的嵌入向量。为了保持数值稳定性，最终会对生成的特征向量进行 $L_2$ 归一化，使其具有统一的尺度。

但是作者没写某个POI类型的embedding是怎么来的。

3.1.2 Point Space Encoder（重点）

在 Space2Vec 中，为了对空间位置（例如二维坐标）进行有效编码，作者提出了一种基于傅里叶变换原理的多尺度位置编码器 —— Point Space Encoder。我们可以将它看作是从大脑中“网格细胞”的周期性空间表示受到启发，结合傅里叶分析构建的一种编码方式。其目标是将任意二维位置向量 $\mathbf{x}\in {\mathbb{R}}^2$ 映射为一个高维的、方向敏感的、尺度可变的空间嵌入向量，用于表示空间中“某处”的语义特征。

傅里叶变换是一种经典的数学工具，它能将一个函数或信号表示为一组正弦函数和余弦函数的加权组合。在空间表示中，这种变换的一个显著优势是：能够通过不同频率的三角波对局部和全局结构进行编码。举个例子，我们可以用如下方式将一个标量坐标位置 $x$ 编码为周期性向量：

$$[\sin (f_1\cdot x),\cos (f_1\cdot x),\sin (f_2\cdot x),\cos (f_2\cdot x),\dots ]$$

其中每个频率 $f_i$ 对应不同的尺度，能够捕捉位置 $x$ 所在的环境在不同“分辨率”下的结构变化。这种编码方式不仅保留了位置之间的相对距离信息，还天然具有周期性，非常适合处理空间数据中重复结构的表达。事实上，Transformer 模型中的位置编码也是这一思想的变体。

在 Space2Vec 中，作者不仅使用多频率的正余弦函数，还引入了多个空间方向进行编码，以模拟生物神经系统中的网格细胞行为。具体来说，作者选择了三个互相夹角为 $120^{\circ }$ 的方向向量：

$${\mathbf{a}}_1=\left[\begin{array}{c}10\end{array}\right],{\mathbf{a}}_2=\left[\begin{array}{c}-\frac{1}{2}\frac{\sqrt{3}}{2}\end{array}\right],{\mathbf{a}}_3=\left[\begin{array}{c}-\frac{1}{2}-\frac{\sqrt{3}}{2}\end{array}\right]$$

对于一个二维空间位置 $\mathbf{x}$，在尺度 $s$ 和方向 $j$ 上的位置编码被定义为：

$$P{E}_{s,j}^{(t)}(\mathbf{x})=\left[\cos \left(\frac{⟨\mathbf{x},{\mathbf{a}}_j⟩}{{\lambda }_{\text{min}}\cdot g^{s/(S-1)}}\right),\sin \left(\frac{⟨\mathbf{x},{\mathbf{a}}_j⟩}{{\lambda }_{\text{min}}\cdot g^{s/(S-1)}}\right)\right]\forall j=1,2,3$$

其中：

• $⟨\mathbf{x},{\mathbf{a}}_j⟩$ 表示 $\mathbf{x}$ 在第 $j$ 个方向上的投影；
• ${\lambda }_{\text{min}}$ 是最小尺度（最高频率）；
• ${\lambda }_{\text{max}}$ 是最大尺度（最低频率）；
• $g=\frac{{\lambda }_{\text{max}}}{{\lambda }_{\text{min}}}$ 是频率缩放比例；
• $s$ 是当前尺度索引，总共有 $S$ 个尺度。

这意味着，在每个尺度下，作者使用三个方向和两种波形（cos 和 sin），共生成 $6$ 个数值，最终在 $S$ 个尺度上拼接得到一个 $6S$ 维的向量作为位置的嵌入表示。

这种编码方式的优势在于它能实现“多尺度空间感知”。换言之，模型不仅能捕捉到空间中局部的微小变化（高频部分），还能同时理解更大范围的结构趋势（低频部分）。此外，相比于传统位置编码（例如 Transformer 中那种分别编码 $x$ 和 $y$ 维度的做法）：

$$P{E}_{s,l}^{(g)}(\mathbf{x})=\left[\cos \left(\frac{x^{[l]}}{{\lambda }_{\text{min}}\cdot g^{s/(S-1)}}\right),\sin \left(\frac{x^{[l]}}{{\lambda }_{\text{min}}\cdot g^{s/(S-1)}}\right)\right]\forall l=1,2$$

Space2Vec 这种六边形方向周期编码方法具有更强的方向敏感性和空间结构表达能力，能模拟出类似于“网格状放电”的神经反应模式，显著提升对空间分布特征的建模能力。

3.2 Decoder

Space2Vec 提出了解码器结构用于空间向量的反向建模，旨在解决两类典型的 GIS 问题：位置建模（Location Modeling）和空间上下文建模（Spatial Context Modeling）。

3.2.1 Location Decoder

其中，Location Decoder 的核心目标是：仅通过一个点的位置向量，就能还原出这个点的语义特征信息。

在实际任务中，这种解码能力非常有用。例如，我们希望模型能仅根据一个地点的经纬度，预测出它的功能类型（如商店、公园、学校等），哪怕该地点没有明确标注标签。因此，Location Decoder 的任务可以理解为：位置 → 语义的学习过程。

具体来说，Location Decoder 被定义为一个前馈神经网络（Feed-forward Neural Network），记作 $De{c}_s$，它的输入是空间编码器输出的位置向量 $\mathbf{e}[{\mathbf{x}}_i]$，输出是重构出的语义特征向量 $\mathbf{e}[{\mathbf{v}}_i]’$。整个过程可以形式化为：

$$\mathbf{e}[{\mathbf{v}}_i]’=De{c}_s({\mathbf{x}}_i;{\theta }_{de{c}_s})=N{N}_{dec}(\mathbf{e}[{\mathbf{x}}_i])$$

这里：

• ${\mathbf{x}}_i$ 表示第 $i$ 个点的空间坐标；
• $\mathbf{e}[{\mathbf{x}}_i]$ 是该点的位置编码结果，通常是由前面介绍的 Point Space Encoder 生成；
• $N{N}_{dec}$ 是解码器神经网络，参数为 ${\theta }_{de{c}_s}$；
• 输出向量 $\mathbf{e}[{\mathbf{v}}_i]’$ 是对该点真实语义嵌入 $\mathbf{e}[{\mathbf{v}}_i]$ 的预测重构。

在训练过程中，作者采用了向量内积（dot product）作为相似性度量方式，通过比较预测向量 $\mathbf{e}[{\mathbf{v}}_i]’$ 与真实语义嵌入 $\mathbf{e}[{\mathbf{v}}_i]$ 的相似度，来优化模型参数。换句话说，目标是最大化它们之间的匹配程度，同时引入其他负样本（即来自其他位置的点的特征向量）作为对比，以增强判别能力。

这种从位置向语义的映射能力，是 Space2Vec 架构中最直接的地理推理方式，体现了“空间结构本身就蕴含语义”的基本假设。

3.2.2 Spatial Context Decoder

除了基于位置的 Location Decoder，Space2Vec 还设计了一个更强大的模块：Spatial Context Decoder，它不仅使用中心点的位置，还结合了其邻近点的空间和语义信息，以更全面地预测该点的语义嵌入向量。这个设计非常适合处理地理信息系统（GIS）中常见的“空间上下文建模”任务，例如：一个位置的功能可能并不只是由自身决定，而是受其邻域环境影响（比如周围都是学校，那中间的点也可能是教育类设施）。

在具体实现中，对于一个中心点 $p_i=({\mathbf{x}}_i,{\mathbf{v}}_i)$，我们考虑它周围的 $n$ 个邻居点 $p_{i1},p_{i2},\dots ,p_{in}$，每个邻居点都有自己的空间编码和语义向量。Spatial Context Decoder 的目标是使用这些邻居点的嵌入信息来重构中心点的语义向量 $\mathbf{e}[{\mathbf{v}}_i]$。

这个过程的整体形式如下：

$$\mathbf{e}[{\mathbf{v}}_i]’=De{c}_c({\mathbf{x}}_i,{\mathbf{e}}_{i1},\dots ,{\mathbf{e}}_{in};{\theta }_{dec})=g\left(\frac{1}{K}\sum _{k=1}^K\sum _{j=1}^n{\alpha }_{ijk}\mathbf{e}[{\mathbf{v}}_{ij}]\right)$$

这里的含义如下：

• $g(\cdot )$ 是激活函数（如 Sigmoid）；
• $K$ 是注意力头（multi-head attention）的数量；
• ${\alpha }_{ijk}$ 是第 $k$ 个注意力头中，中心点 $p_i$ 对第 $j$ 个邻居点的注意力权重；
• $\mathbf{e}[{\mathbf{v}}_{ij}]$ 是第 $j$ 个邻居点的语义嵌入。

这个结构类似于图注意力网络（Graph Attention Network, GAT），它将多个邻居点的特征通过加权平均聚合，以形成中心点的表示。每个注意力头都学习不同的关注模式，然后平均后作为最终输出。

注意力权重 ${\alpha }_{ijk}$ 的计算方式：

注意力机制的关键是计算每个邻居的重要性，即注意力得分 ${\alpha }_{ijk}$。Space2Vec 中的注意力权重是通过 LeakyReLU 激活函数计算的“相似度评分”，公式如下：

$${\sigma }_{ijk}=LeakyReLU\left({\mathbf{a}}_k^T\left[\mathbf{e}[\mathbf{v}i{]}_{init};\mathbf{e}[{\mathbf{v}}_{ij}];\mathbf{e}[{\mathbf{x}}_i-{\mathbf{x}}_{ij}]\right]\right)$$

解释如下：

• $\mathbf{e}[{\mathbf{v}}_i{]}_{init}$ 是当前中心点的特征初始估计值（我们下面会讲它从哪来）；
• $\mathbf{e}[{\mathbf{v}}_{ij}]$ 是邻居点的语义向量；
• $\mathbf{e}[{\mathbf{x}}_i-{\mathbf{x}}_{ij}]$ 是中心点与邻居点之间的位移编码（表示方向和距离）；
• ${\mathbf{a}}_k$ 是第 $k$ 个注意力头的参数向量；
• LeakyReLU 是一种非线性激活函数。

然后再将这些打分通过 softmax 标准化为权重：

$${\alpha }_{ijk}=\frac{\exp ({\sigma }_{ijk})}{{\sum }_{o=1}^n\exp ({\sigma }_{iok})}$$

这样，模型就能自动学习：哪个邻居点在当前任务中最“相关”，而不是平均处理所有邻居。

关于初始语义估计 $\mathbf{e}[{\mathbf{v}}_i{]}_{init}$：

由于目标是预测 $\mathbf{e}[{\mathbf{v}}_i]$，而注意力打分又用到了它，所以作者引入了一个初始估计值 $\mathbf{e}[{\mathbf{v}}_i{]}_{init}$，它是通过另一层类似的注意力机制得到的，但不包含 $\mathbf{e}[{\mathbf{v}}_i]$ 本身，只用邻居信息：

$$\sigma {’}_{ijk}=LeakyReLU\left({\mathbf{a}}_k^T\left[\mathbf{e}[{\mathbf{v}}_{ij}];\mathbf{e}[{\mathbf{x}}_i-{\mathbf{x}}_{ij}]\right]\right)$$

和前面类似，但此时不使用 $\mathbf{e}[{\mathbf{v}}_i{]}_{init}$ 作为输入，从而避免信息泄露。最终形成初始估计 $\mathbf{e}[{\mathbf{v}}_i{]}_{init}$ 后，才会用于${\sigma }_{ijk}=LeakyReLU\left({\mathbf{a}}_k^T\left[\mathbf{e}[\mathbf{v}i{]}_{init};\mathbf{e}[{\mathbf{v}}_{ij}];\mathbf{e}[{\mathbf{x}}_i-{\mathbf{x}}_{ij}]\right]\right)$的注意力打分。

3.3 无监督学习

Space2Vec 的训练是以无监督方式进行的，也就是说，它并不依赖人工标注的类别标签，而是利用地理点本身的位置与空间邻居信息，通过构造预测任务来学习语义表示。模型的核心任务是：让每个点能够“预测出自己是谁”，即仅通过自身的位置和邻域，重构出自己的语义表示。

整个训练过程以最大化自信息一致性为目标，模型结构由两部分组成：

• Encoder（编码器）：将空间位置和属性嵌入为向量
• Decoder（解码器）：从编码向量重构语义嵌入

1. 编码器：将位置与类型信息转换为向量表示

1.1 空间编码器（Point Space Encoder）

输入为一个点的位置坐标 ${\mathbf{x}}_i\in {\mathbb{R}}^2$，编码器 $En{c}^{(x)}$ 使用傅里叶编码思想，对多个尺度下的位置投影应用正弦/余弦变换，输出一个高维位置嵌入向量 $\mathbf{e}[{\mathbf{x}}_i]\in {\mathbb{R}}^{d^{(x)}}$。该模块的参数包括：

• 多尺度位置频率控制参数（隐含于编码函数中）
• 若使用神经网络结构包裹（如文中 $NN(\cdot )$），则包含网络权重 ${\theta }_{enc}^{(x)}$

1.2 语义编码器（Point Feature Encoder）

每个点 $p_i$ 还携带一个 POI 类型集合 ${\gamma }_1,\dots ,{\gamma }_H$，每个类型对应一个可训练的向量 ${\mathbf{t}}_h^{(\gamma )}\in {\mathbb{R}}^{d^{(v)}}$。这些类型向量通过平均得到语义向量：

$$\mathbf{e}[{\mathbf{v}}_i]=\frac{1}{H}\sum _{h=1}^H{\mathbf{t}}_h^{(\gamma )}$$

这些类型向量 ${\mathbf{t}}_h^{(\gamma )}$ 是模型参数的一部分，会在训练过程中更新。这一部分参数集合记作 ${\theta }_{enc}^{(v)}$。

2. 解码器：从编码中重建语义表示

模型的目标是根据编码向量 $\mathbf{e}[{\mathbf{x}}_i]$ 或其邻域特征，预测出该点的语义向量 $\mathbf{e}[{\mathbf{v}}_i]’$。

2.1 Location Decoder

Location Decoder 是一个前馈神经网络，用于根据位置编码预测语义向量：

$$\mathbf{e}[{\mathbf{v}}_i]’=De{c}_s({\mathbf{x}}_i;\theta de{c}_s)=N{N}_{dec}(\mathbf{e}[{\mathbf{x}}_i])$$

参数 ${\theta }_{de{c}_s}$ 是该网络的权重，会被训练更新。

2.2 Spatial Context Decoder

该模块融合了邻域中多个点的位置 + 语义信息，通过注意力机制加权聚合邻居的语义向量，最终预测中心点 $p_i$ 的语义嵌入 $\mathbf{e}[{\mathbf{v}}_i]’$。整个过程涉及两个阶段：

• 先估计初始值 $\mathbf{e}[{\mathbf{v}}_i{]}_{init}$
• 然后通过多头注意力机制，聚合邻居的表示得到最终预测

该模块包含多组注意力头参数 ${\mathbf{a}}_k$，以及聚合网络参数 ${\theta }_{de{c}_c}$，也会在训练中被更新。

3. 损失函数设计：让预测语义尽量接近真实语义

训练的核心是一个匹配任务。我们希望预测出的语义向量 $\mathbf{e}[{\mathbf{v}}_i]’$ 与真实语义 $\mathbf{e}[{\mathbf{v}}_i]$ 尽可能一致。

这可以通过最大化 log-likelihood 实现：

$${\mathcal{L}}_{\mathcal{P}}(\theta )=-\sum _{p_i\in \mathcal{P}}\log \frac{\exp \left(\mathbf{e}[{\mathbf{v}}_i{]}^T\mathbf{e}[{\mathbf{v}}_i]’\right)}{{\sum }_{p_o\in \mathcal{P}}\exp \left(\mathbf{e}[{\mathbf{v}}_o{]}^T\mathbf{e}[{\mathbf{v}}_i]’\right)}$$

解释如下：

• 分子是预测语义和真实语义的匹配度（通过内积衡量）；
• 分母是所有可能候选点中与预测向量的匹配度；
• 最终目标是让正确点的相似度最大，其他点的最小。

4. 负采样优化：提升训练效率

由于分母计算代价太大，作者采用了负采样（Negative Sampling）方法，改写损失为：

L ’ P ( θ ) = ∑ p i ∈ P ( log ⁡ σ ( e [ v i ] T e [ v i ] ’ ) + 1 ∣ N i ∣ ∑ p o ∈ N i log ⁡ σ ( − e [ v o ] T e [ v i ] ’ ) ) \mathcal{L}’_{\mathcal{P}}(\theta) = \sum_{p_i \in \mathcal{P}} \left( \log \sigma\left(\mathbf{e}[\mathbf{v}_i]^T \mathbf{e}[\mathbf{v}_i]’\right) + \frac{1}{|\mathcal{N}_i|} \sum_{p_o \in \mathcal{N}_i} \log \sigma\left(-\mathbf{e}[\mathbf{v}_o]^T \mathbf{e}[\mathbf{v}_i]’\right) \right) L’P​(θ)=pi​∈P∑​ ​logσ(e[vi​]Te[vi​]’)+∣Ni​∣1​po​∈Ni​∑​logσ(−e[vo​]Te[vi​]’) ​

其中：

• ${\mathcal{N}}_i$ 是为 $p_i$ 随机采样的一组负样本；
• $\sigma (x)$ 是 Sigmoid 函数；
• 第一项是“正匹配得分”，第二项是“负样本惩罚”。

这样，大大减少了每轮训练的计算量。

5. 训练过程：端到端参数更新

模型参数包括：

• 位置编码器参数 ${\theta }_{enc}^{(x)}$；
• 类型嵌入矩阵（每个 ${\mathbf{t}}_h^{(\gamma )}$）；
• 解码器参数（$N{N}_{dec}$ 或注意力网络）${\theta }_{dec}$；

所有这些参数都在损失函数的反向传播过程中被更新。这构成了一个完整的端到端无监督学习框架。

最终，模型能够学会：

• 编码器：如何将位置和类型嵌入为结构化语义向量；
• 解码器：如何从编码中预测出地点的真实语义；
• 语义 embedding 表达：如何让同一类型的点聚在一起，不同类型的点远离彼此。