【BFS】P1379 八数码难题

P1379 八数码难题

点击跳转：洛谷P1379

题目描述

在 $3\times 3$ 的棋盘上，摆有八个棋子，每个棋子上标有 $1$ 至 $8$ 的某一数字。棋盘中留有一个空格，空格用 $0$ 来表示。空格周围的棋子可以移到空格中。要求解的问题是：给出一种初始布局（初始状态）和目标布局（为了使题目简单,设目标状态为 $123804765$），找到一种最少步骤的移动方法，实现从初始布局到目标布局的转变。

输入格式

输入初始状态，一行九个数字，空格用 $0$ 表示。

输出格式

只有一行，该行只有一个数字，表示从初始状态到目标状态需要的最少移动次数。保证测试数据中无特殊无法到达目标状态数据。

输入输出样例 #1

输入 #1

283104765

输出 #1

4

说明/提示

样例解释

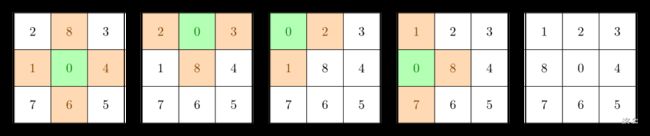
图中标有 $0$ 的是空格。绿色格子是空格所在位置，橙色格子是下一步可以移动到空格的位置。如图所示，用四步可以达到目标状态。

并且可以证明，不存在更优的策略。

思路讲解：BFS和DFS的选择

问题：为什么这题要用BFS而不是DFS?
这道题的目标是：从初始状态出发，找到达到目标状态 123804765 所需的最少移动步数
BFS 的特点：
按“步数层级”扩展节点：第一层是 0 步，第二层是 1 步，第三层是 2 步……
所以第一次到达目标状态的路径就是最短路径
BFS 可以天然用于 “最少步数” “最短路径” 类问题.
对比DFS：
DFS 会优先探索一条路径到底，哪怕已经走了 200 步，它也不会停
最终即使找到目标状态，也不保证是最短路径
如果选择DFS解题需要手动记录当前路径长度、剪枝、比较多个路径，写法更复杂，效率更差

BFS和DFS的使用场景

先抽象地理解他们俩的工作原理：

• DFS：
  你一头扎进一条通道，不停地往里走，走到死胡同才回头换一条……可能先绕了 100 圈，最后才找对路。
• BFS：
  你站在入口，先走一步能到哪？再走两步能到哪？……这样层层扩展，第一次到达出口的位置一定是最短的路径。

应用场景：

• BFS：
  最短步数、最短距离、最少操作
  例如：八数码问题、迷宫走法、图最短路径
• DFS：
  全路径遍历、组合、排列、某种状态是否存在
  例如：数独、括号生成、全排列、N皇后、图是否连通

BFS的具体实现

在写BFS的时候，思路和DFS是不同的，DFS主要是基于递归实现的，而BFS主要是基于队列来模拟广度优先搜索，多做几题熟悉BFS的模板就好写了。

本题核心思想

这一题的核心思想就是将字符串中的’0’(出口位置)的坐标转换成实际在二维数组中的坐标，然后在二维数组中模拟上下左右的移动，判断合法后再将移动后的坐标转换成一维坐标(在字符串中的坐标)，然后在字符串中进行操作。这里将这种操作简单地称为二维坐标转一维度坐标，一维坐标转二维度坐标，注意：它的实现要基于0-base。

如果通过二维数组去模拟这个过程，将会大幅增加时间复杂度和空间复杂度。那么如何做优化呢？
我们可以观察二维坐标和一维度坐标的横纵坐标间的规律，得出这样一个公式：
在一个n * m的二维数组中，
二维坐标(x,y)的一维坐标 pos = x * m + y;
一维坐标pos的二维坐标x = pos / 3 , y = pos % 3。

题解

#include
#include
#include
using namespace std;

string s;
string aim = "123804765";
unordered_map<string,int> mp;

int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};

void bfs()
{
	queue<string> q;
	q.push(s);
	mp[s] = 0;
	
	while(q.size())
	{ 
		string t = q.front(); q.pop();
		//pos找0的位置 
		int pos = 0;
		while(t[pos] != '0') pos++;
		//根据pos求二维坐标
		int x = pos / 3, y = pos0 % 3; 
		for(int i=0;i<4;i++)
		{
			string tmp = t;
			//求(x,y)的新坐标 
			int a = x + dx[i], b = y + dy[i];
			if(a >= 0 && a <= 2 && b >= 0 && b <= 2)
			{
				//(a,b)坐标合法，根据(a,b)求一维坐标 
				int newpos = 3 * a + b; 
				swap(tmp[newpos],tmp[pos]);
				//不能访问已经处理过的情况 
				if(mp.count(tmp)) continue;			
				q.push(tmp); 
				mp[tmp] = mp[t] + 1;				
				if(tmp == aim) return; 
			
			}
		}
	} 
}

int main()
{
	cin >> s;
	
	bfs();
	
	cout << mp[aim] << endl;
	return 0;
} 

错误的思路

有的同学可能会想，二维坐标向上下左右四个方向移动在字符串中的规律体现是是分别移动了-1，1，-3，3个单位，直接定义一个在字符串内水平的方向向量来移动这样不行吗？

在理论上，八数码问题的空格（0）可以向上下左右移动，转换为一维索引变化如下：

• 左移：-1
• 右移：+1
• 上移：-3
• 下移：+3

这些偏移量本身是对的，但如果我们只判断新下标是否在 [0, 8] 内，就会导致问题。

举个例子：
位置索引：
0 1 2
3 4 5
6 7 8
假设当前状态中空格的位置是下标 3，也就是棋盘中的 第 2 行第 1 列
此时如果你左移（-1），计算出：int newpos = 3 + (-1) = 2;
虽然 2 落在 [0, 8] 中，但它在棋盘上的位置是 第 1 行第 3 列

• 原位置：第 2 行第 1 列（(1, 0)）
• 新位置：第 1 行第 3 列（(0, 2)）
  这就意味着你“穿越了一整行”，这在八数码的移动中是不允许的。

但是这种方法就完全错误了吗？其实在此基础上加上边界判断就可以了。

正确做法：左右移动前额外加判断

// 左移
if (pos % 3 != 0) 
{
    int newpos = pos - 1;
    // ...
}

// 右移
if (pos % 3 != 2) 
{
    int newpos = pos + 1;
    // ...
}

正确代码

#include
#include
#include
using namespace std;

string s;
string aim = "123804765";
unordered_map<string,int> mp;

int d[] = {-1,1,-3,3};

void bfs()
{
	queue<string> q;
	q.push(s);
	mp[s] = 0;
	
	while(q.size())
	{
		string t = q.front(); q.pop();
		int pos = 0;
		while(t[pos] != '0') pos++;
		for(int i=0;i<4;i++)
		{
			string tmp = t;	
			//当向左移的时候pos恰好又等于0 或者 向右移的时候pos恰好等于2 就跳过
			if(d[i] == -1 && pos % 3 == 0 || d[i] == 1 && pos % 3 == 2) continue;
			int newpos = pos + d[i];
			if(newpos >= 0 && newpos <= 8)
			{
				swap(tmp[newpos],tmp[pos]);
				if(mp.count(tmp)) continue;
				q.push(tmp); 
				cout << tmp << endl;
				cout << mp[tmp] << endl;
				mp[tmp] = mp[t] + 1;
				if(tmp == aim) return;				
			}
		}
	} 
}

int main()
{
	cin >> s;
	
	bfs();
	
	cout << mp[aim] << endl;
	return 0;
}