动态规划算法：01背包问题（子集问题）

前言-01背包问题

有两个问题：
问题1：
小明有一个背包，背包容积为v，有m个物品，其中第i个物品的价值为val[i]，体积为t[i]，每样物品只有一个，请问如何装物品能让背包内的物品价值最大？

看过我回溯算法篇章的朋友们应该会有一些思路，这个其实是一个标准的子集问题，我们要从所有物品中挑选出价值最大的若干物品，且要可以装进背包中。（回溯算法（1）：子集问题）

问题2：
小明有一个背包，背包容积为v，有m个物品，其中第i个物品的价值为val[i]，体积为t[i]，每样物品只有一个，选若干物品装入背包内，请问背包内的物品可能的最大价值是多少？

详细观察两个问题的朋友会发现，这两题描述了一个相似的场景，但是问题二需要的信息更少，仅要求我们返回最大的价值，不需要列出对应的物品。使用回溯算法的子集模板固然可以解决问题，但是这样在考试中大概率会超时，因为回溯算法本质上是一种暴力求解。我们是不是有一种更好，更快的方法来处理这种问题呢？这就是我们今天要介绍的一个方法类型：子集类动态规划。对于这种每个物品只有一个的情况，被称为01背包。

01背包问题

针对问题2：
小明有一个背包，背包容积为v，有m个物品，其中第i个物品的价值为val[i]，体积为t[i]，每样物品只有一个，选若干物品装入背包内，请问背包内的物品可能的最大价值是多少？

分析

大家不要钻牛角尖，这种动态规划问题如果没有接触过是很难想出来的，我在这里稍微引导一下大家。
动态规划最重要的就是确定dp数组。一般dp数组最后一个元素的值就是我们要的结果。由于这道题的dp数组没有基础真的很难想到，因此我在这里直接给出dp数组的定义，大家记下来就好，千万别钻牛角尖。

dp数组的定义：
dp[i][j]：从第0个物品到第i个物品中选择物品，装进容量为j的背包中可能得到的最大的总价值。
怎么样，如果我不揭晓答案，大家能不能想到呢？

状态转移关系的确定
确定了dp[i][j]的含义，接下来就是推到状态转移方程了。这个过程中要时刻谨记dp[i][j]的含义。
我们来看一下dp[i][j]是怎么得来的，我们首先要假设一点：之前的状态是已知的。结合定义，dp[i][j]描述的是容积为j的背包。
（1）当j时，我们无论如何也无法将第i个物品放入背包，因此我们能得到的最大的价值就是我们之前求得的dp[i-1][j]。复述一遍定义，dp[i-1][j]是从0到i-1个物品中选取一些物品放入容积为j的背包，可能得到的最大的价值。
（2）当j≥t[i]时，背包的容积为大于第i个物品的体积，我们有可能放入第i个物品，因此我们就要多考虑一种情况。当我们放入物品i，就会获得物品i的价值，但背包剩余的容积就是( j - t[i] )，也就是说留给编号为0到i-1的物品的空间只有( j - t[i] )，这种条件下能得到的最大价值是( val[i] + dp[i-1][j-t[i]] )。当然我们也可以选择不放入第i个物品，那么我们能得到的最大价值仍然是dp[i-1][j]。我们应该比较两者价值，取大的值。
用伪代码表示dp[i][j]的状态转移过程：

if(j < t[i]) dp[i][j] = dp[i-1][j];		// 根本装不下第i个物品，不用考虑，直接继承
else dp[i][j] = max(dp[i-1][j-t[i]] + val[i], dp[i-1][j]);	// 比较后决定是否放入第i个物品

下图展示了dp[i][j]的推导方向，只要知道dp数组第i-1行的元素的值，就可以推导出dp[i][j]。

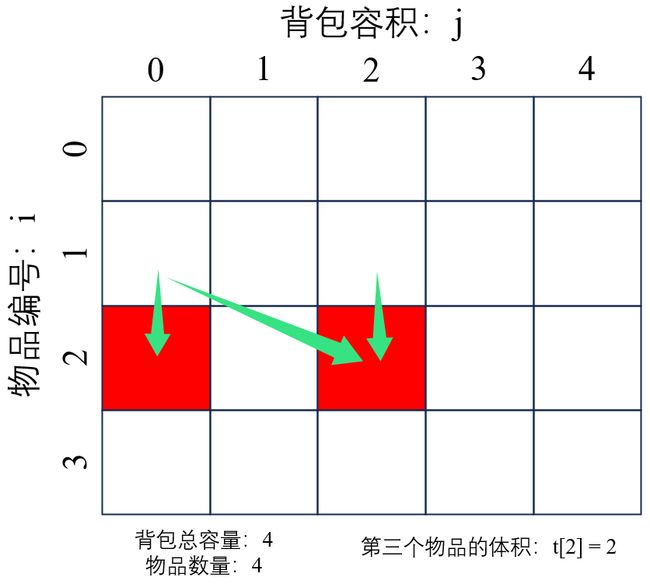
dp数组的初始化：
在上面的论述中我们知道了，只要知道上一行，就可以推导出当前行，因此我们对dp初始化时就只需要将第0行初始化即可。
（1）当j时，背包装不下第0个物品，总价值为0。
（2）当j≥t[0]时，背包可以装下第0个物品，背包内最大价值为val[0]。
伪代码(背包容积为v)：

for(int j = 0; j<=v; j++) {
	if(j < t[0]) dp[0][j] = 0;
	else dp[0][j] = val[0];
}

有了上述所有的推到，我们可以尝试写代码了：

代码

#include 
#include 
using namespace std;

int main() {
	int m, v; // m个物品， 背包容积为v
	cin >> m >> v;
	vector<int> t(m, 0);
	vector<int> val(m, 0);
	for(int i = 0; i < m; i++ ) {
		cin >> t[i] >> val[i];
	}
	vector<vector<int>> dp(m, vector<int>(v+1, 0));
	for(int j = 0; j <= v; j++) {
		if(j < t[0]) dp[0][j] = 0;
		else dp[0][j] = val[0];
	}
	
	for(int i = 1; i < m; i++) {
		for(int j = 0; j <= v; j++) {
			if(j < t[i]) dp[i][j] = dp[i-1][j];
			else dp[i][j] = max(dp[i-1][j], dp[i-1][j-t[i]] + val[i]);
		}
	}
	
	cout << dp.back().back() <<endl;
	return 0;
}

维度压缩

if(j < t[i]) dp[i][j] = dp[i-1][j];		// 根本装不下第i个物品，不用考虑，直接继承
else dp[i][j] = max(dp[i-1][j-t[i]] + val[i], dp[i-1][j]);	// 比较后决定是否放入第i个物品

假设我们不加入第i个物品，那么我们发现其实dp[i][:]的值与上一行的dp[i-1][:]完全相同。
我们不放大胆一些，去掉第一个维度，dp数组变为：dp[j] = dp[j];，直接可以省略。
当我们加入第i个物品时：dp[j] = max(dp[j-t[i]] + val[i], dp[j]);。
这时有同学会提出疑问，这样的话我的j从0到v遍历的时候岂不是就会拿到改变后的dp[j-t[i]]值，而二维状态下的dp[i-1][j-t[i]]是不会变化的，这会出现问题。
的确有这个问题，但是这是在一个错误的前提下，暨j从0到v遍历。但是我们来观察一下dp推导路径图，研究dp的推导方向，我们发现，实际上dp是不依赖于同行的元素的，只要保证上一行的元素已知，就可以推导出当前行的元素。

降低维度后，上一行的元素就是dp数组本身，因此我们可以选择从右侧向左侧遍历，这样我们的dp[j-t[i]]值就不会被污染，因为(j-t[i]) < j，需要后遍历，遍历到的时候计算已经完成了，如下图所示。

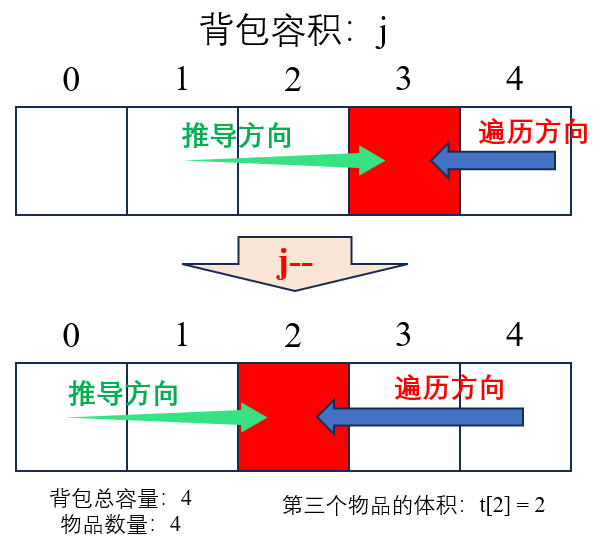
维度压缩不仅可以节约空间，还可以免去dp初始化的工作，仅需要vector初始化时将dp全部置0即可。之前因为当前行依赖于上一行，因此必须将第0行初始化并另i从1开始向后遍历，不然dp[i][j] = dp[i-1][j]在i=0时就会报错。但是现在压缩维度或，所有的计算都在一行内完成，也自然不需要初始化了。

维度压缩后代码

#include 
#include 
using namespace std;

int main() {
	int m, v; // m个物品， 背包容积为v
    cin >> m >> v;
	vector<int> t(m, 0);
	vector<int> val(m, 0);
	for(int i = 0; i < m; i++ ) {
		cin >> t[i] >> val[i];
	}
	
	vector<int> dp(v+1, 0);	// 压缩后不再需要初始化
	
	for(int i = 0; i < m; i++) {
		for(int j = v; j >= 0; j--) {
			if(j < t[i]) dp[j] = dp[j];		// 这一行其实没有用，为了让大家更加清晰
			else dp[j] = max(dp[j], dp[j-t[i]] + val[i]);
		}
	}
	
	cout << dp.back() <<endl;
	return 0;
}

问题拓展

小明有若干面值的硬币nums，小明需要买一个物品需要m元，小明想知道自己的硬币能否刚好凑够m元，如果可以，那么需要的最少硬币数量是多少。
注，nums中每个元素代表一枚对应面值的硬币。

问题分析：这道题其实也是子集类问题，（1）能不能拿出一部分硬币刚好凑够m元，（2）需要的最少硬币个数。从本质来看，他们都是要求一个子集的性质，一个是子集的大小，一个是子集的总和，因此都可以用我上面提到的思路来解决。

dp数组定义：
还是设计一个dp数组，具有两个维度，初始化为vector> dp(nums.size(), m+1)。
其中第一个维度为硬币个数，第二个维度为目标价值总和。现在大家能否结合题目的要求尝试说出dp[i][j]的含义呢？
我来揭晓答案，dp[i][j]为从0到i个硬币中凑够总价值j需要的最少硬币数量。

状态转移：
至于dp[i][j]的转移过程呢，大家不妨先自己思考一下，再向下看。
我来揭晓答案，dp[i][j]的转移分为两种情况：
（1）当j时，暨需要的总价值小于第i个硬币的面值时，第i枚硬币的加入不会影响结果，因此dp[i][j] = dp[i-1][j]。
（2）当j≥nums[i]时，我们可以选择将第i枚硬币放入，那么第0到第i-1枚硬币就要凑够面值j-nums[i]，如果可以满足凑够，那这种情况下需要的硬币数量就是1+dp[i-1][j-nums[i]]。如果不放入第j枚金币，那么结果仍然为dp[i-1][j]。需要比较这两种情况下的大小。
伪代码：

if(j < nums[i] ) dp[i][j] = dp[i-1][j];
else(j >= nums[j] && dp[i-1][j-nums[i]] != INT_MAX])	// 我们要确认前i-1个硬币能否凑够面值j-nums[i] 
	dp[i][j] = min(dp[i-1][j-nums[i]] + 1, dp[i-1][j])

实际上大家可以发现其实这里和上面的背包问题没有太大差别。

dp初始化：
直接结合代码展示：

vector<vector<int>> dp(nums.size(), vector<int>(m+1, INT_MAX)); 	// 默认初始化为INT_MAX
// 初始化第一行
dp[0][0] = 0;	// 凑够面值为0仅需要0枚硬币
if(m >= nums[0]) dp[0][nums[0]] = 1;	// 如果目标值大于第一枚的面值，则凑够面值nums[0]仅需要1枚硬币

完整代码：

#include 
#include  
#include 
using namespace std;

int main() {
	int m, n;
	cin >> m >> n;
	vector<int> nums(n);
	for(int i = 0; i< n; i++) cin >> nums[i];
	
	vector<vector<int>> dp(n, vector<int>(m+1, INT_MAX));
	dp[0][0] = 0;
	if(m >= nums[0]) dp[0][nums[0]] = 1;

	for(int i = 1; i < n; i++) {
		for(int j = 0; j <= m; j++) {
			if(j < nums[i]) dp[i][j] = dp[i-1][j];
			else if(j >= nums[i] && dp[i-1][j-nums[i]] != INT_MAX) 
				dp[i][j] = min(dp[i-1][j], dp[i-1][j-nums[i]] + 1);
		}
	}
	
	cout << dp.back().back() <<endl;
	return 0;
}

维度压缩：
这里也是可以将dp数组由二维降为一维，这个就交给大家了。

小节

通过动态规划解决子集问题是一个效率更高的解决方案，针对题目中具体的问题，我们基于dp[i][j]不同的定义，并调整dp[i][j]的取值条件，可以解决不同的问题。
下一节我会对这个问题进行进一步的拓展。
动态规划算法：完全背包类问题