一桶泡面的时间解决高频面试算法题——螺旋矩阵

一、题目描述——螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。  

示例 1：

lua

代码解读

复制代码

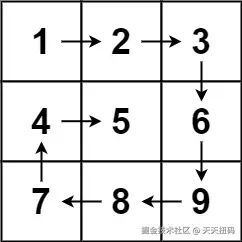
输入： matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出： [1,2,3,6,9,8,7,4,5]

示例 2：

lua

代码解读

复制代码

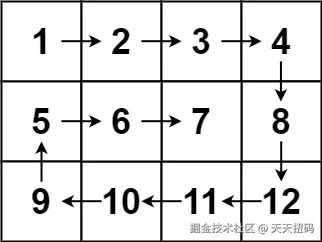
输入： matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出： [1,2,3,4,8,12,11,10,9,5,6,7]

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

二、题解

js

代码解读

复制代码

/** * @param {number[][]} matrix * @return {number[]} */ var spiralOrder = function(matrix) { const result = []; let top = 0; let bottom = matrix.length - 1; let left = 0; let right = matrix[0].length - 1; let direction = 0; // 0: right, 1: down, 2: left, 3: up while (top <= bottom && left <= right) { if (direction === 0) { // Right for (let i = left; i <= right; i++) { result.push(matrix[top][i]); } top++; } else if (direction === 1) { // Down for (let i = top; i <= bottom; i++) { result.push(matrix[i][right]); } right--; } else if (direction === 2) { // Left for (let i = right; i >= left; i--) { result.push(matrix[bottom][i]); } bottom--; } else if (direction === 3) { // Up for (let i = bottom; i >= top; i--) { result.push(matrix[i][left]); } left++; } direction = (direction + 1) % 4; } return result; };

核心思想

这道题的核心思想是模拟螺旋轨迹，通过不断收缩矩阵的边界，并按照预定义的顺序（右、下、左、上）逐层遍历矩阵元素。 关键在于维护好四个边界变量（top, bottom, left, right）以及当前遍历的方向（direction），并根据方向更新边界。

详细步骤

1. 初始化：

   • result: 一个空数组，用于存储螺旋顺序遍历的元素。
   • top: 初始值为 0，代表矩阵的上边界。
   • bottom: 初始值为 matrix.length - 1，代表矩阵的下边界。
   • left: 初始值为 0，代表矩阵的左边界。
   • right: 初始值为 matrix[0].length - 1，代表矩阵的右边界。
   • direction: 初始值为 0，代表当前遍历的方向，0表示向右，1表示向下，2表示向左，3表示向上。

2. 循环遍历（while loop）：

   • 条件：top <= bottom && left <= right。 只有当上边界小于等于下边界，且左边界小于等于右边界时，才继续循环。这意味着还有未遍历到的矩阵部分。

3. 基于方向的遍历 (if-else if)：

   • 根据 direction 的值，选择不同的遍历方式：

     • direction === 0 (向右):

       • 使用 for 循环，从 left 遍历到 right，将 matrix[top][i] 添加到 result 数组中。 这表示遍历当前上边界的所有元素。
       • top++: 将上边界向下移动一行，准备遍历下一层。

     • direction === 1 (向下):

       • 使用 for 循环，从 top 遍历到 bottom，将 matrix[i][right] 添加到 result 数组中。 这表示遍历当前右边界的所有元素。
       • right--: 将右边界向左移动一列，准备遍历下一层。

     • direction === 2 (向左):

       • 使用 for 循环，从 right 遍历到 left（注意是倒序遍历），将 matrix[bottom][i] 添加到 result 数组中。 这表示遍历当前下边界的所有元素。
       • bottom--: 将下边界向上移动一行，准备遍历下一层。

     • direction === 3 (向上):

       • 使用 for 循环，从 bottom 遍历到 top（注意是倒序遍历），将 matrix[i][left] 添加到 result 数组中。 这表示遍历当前左边界的所有元素。
       • left++: 将左边界向右移动一列，准备遍历下一层。

4. 更新方向：

   • direction = (direction + 1) % 4: 在每次完成一个方向的遍历后，使用取模运算更新 direction 的值。 % 4 保证 direction 的值始终在 0, 1, 2, 3 之间循环，实现顺时针方向的切换。

5. 返回结果：

   • 循环结束后， result 数组中存储了矩阵螺旋顺序的所有元素，将其返回。

三、结语

再见！

链接：https://juejin.cn/post/7496369162485055503