Linux内核基数树应用分析
Linux内核基数树应用分析
基数树(Radix tree)可看做是以二进制位串为关键字的trie树,是一种多叉树结构,同时又类似多层索引表,每个中间节点包含指向多个节点的指针数组,叶子节点包含指向实际对象的指针(由于对象不具备树节点结构,因此将其父节点看做叶子节点)。
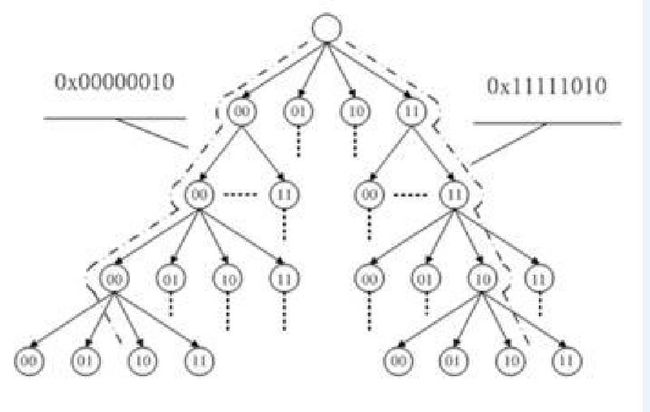
图1是一个基数树样例,该基数树的分叉为4(2^2),树高为4,树的每个叶子结点用来快速定位8位文件内偏移,可以定位4x4x4x4=256(叶子节点的个数)页,如:图中虚线对应的两个叶子结点的路径组成值0x00000010和0x11111010,指向文件内相应偏移所对应的缓存页。
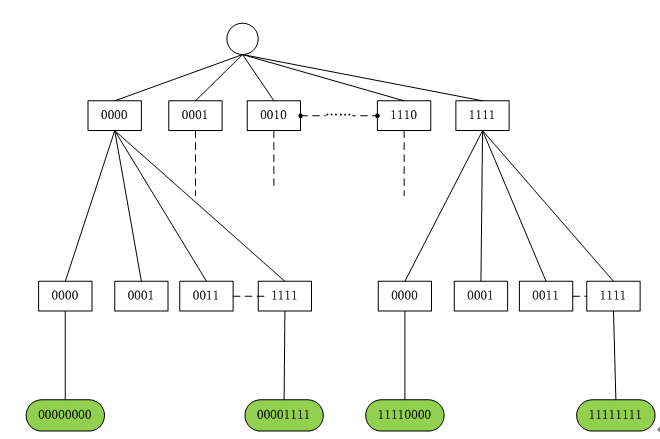
在Linux内核中,基数树用于将对象的句柄id或页索引index映射转化为指向对象的指针(具体来说是转化为一些列有指针组成的路径),这是通过把id分段后作为各层节点的指针数组(以下将指针数组的项成为slot)的索引而达到检索的目的。分段通常使用将id右移指定位数后和指定长度的位掩码相与获得,如(id>>n)&IDR_MASK。比如一个32位的id值,按4位一分段的方法,可以化为8个位串(每个含4位),从高位到低位分别作为1~8层节点的slot索引,通过上一层节点的slot索引得到指向下一层节点的指针,如此直到最后一层,此时索引指向最终对象。如图2所示,为id为8位,按4位分一段的方法,可以构成一个2层的基数树,最下层共有(2^4)*(2^4)=2^8=256个叶子节点,所以功能存放256个对象,并且对象的最大id为256-1=255(id从0开始)。
图2
从这个角度讲,基数树中对象的检索要比固定数组稍慢一些,但是其使用了时间换空间的思想.非常适用于节点数动态变化较大的场合,而它的时间复杂度也是可以接受的,达到O(log2nN),其中2n为每个节点的指针槽数,而n对应分段掩码的位长。
1. 基数树在Linux内核中的应用
1.1 文件缓存页管理
在较早版本的内核中(比如2.4.0),文件页缓存是通过共同的散列表page_hash_table组织的(根据缓存页对应的index进行hash),通过散列表是能较快地搜索到指定文件的指定页,而且没有太多的额外内存消耗,但是其弊端也是显见的,因为所有访问文件都通过同一个散列表缓存页,而查询时都通过自旋锁pagecache_lock,因此就降低了多进程的并发访问性能,在特定场合下是不可忍受的。因此,在2.6内核中用各文件地址空间自行管理缓存页.从而使各文件的页搜寻工作互不影响,提高了并发性能。“Linux2.6内核的文件页是通过基数树管理的,而页索引决定了其在树中的位置。文件地址空间对象的数据结构如下:
struct address_space{
struct inode *host; /*owner:inode,bIock_device*/
struct radix_tree_root pagetree;
)
其中page_tree即指向基数树的根,该指针指向radix_tree_root结构。
struct radix_tree_root{
unsigned int height; //树的高度
gfp_t gfp_mask;
struct radix _tree_ node *rnode; //指向基数树的根节点
};
rnode指向基数树的根节点,根节点是一个radix_tree_node结构。
struct radix_tree_node{
unsigned int heigh; /*Height from the bottom*/
unsigned int count;
struct rcu_head rcu_head;
void *slots[RADlX_TREE_MAP_SIZE];
unsigned Iong tags[RADIX_TREE_MAX_TAGS][RADIX_TREE_TAG_LONGS];
};
height为节点的高度,count指示孩子节点数(也即非空槽位数),slots为子节点指针数组(对于叶节点,则指向对应的页结构),tags数组使用位图分别指示各子树是否包含有对应标志的页。这两个标志分别是脏和写回。
#define PAGECACHE TAG DIRTY 0
#define PAGECACHE 1_AG VVRlTEBACK 1
1.2 进程问通信ipc对象管理
较早内核(如2.6.11)中的ipc对象(比如共享内存对象shm)是用固定数组管理的(对象id为数组的下标),这有一个缺陷,就是当对象数量剧增,原有数组对象数不够时就要通过grow_ary()重新分配新的数组,然后是新旧数组间的内容拷贝,当对象数量变化较大时就要面临数组的频繁分配和释放,这对性能是不利的,因此在2.6.24中ipc对象改用基数树idr管理,虽然通过idr定位对象不像数组那么直接(时间复杂度为树的高度),但是换取了很好的动态性能,增加对象时不会面临大规模的内存分配,只需要创建一个或几个(扩展树时)树节点,并且获取空闲id的性能比数组要好,这直接影响了插入新对象的速度。idr结构用于管理包含ipc对象的基数树,以对象id为索引:
struct idr{
struct idr_Iayer *top;
struct idr_Iayer *id_free;
int Iayers;
int id_free_ cnt;
spinlock_t lock;
};
其中idr_layer是树节点结构,top指向根节点,layers是树的高度,id_free维护一个临时的空闲节点链表,id_free_cnt指示空闲链表中的节点数。
2. 代码分析
2.1 Linux\lib\radix-tree.c
(1) 树高度和最大索引的转换:
static __init unsigned long__maxindex(unsigned int height)
{
unsigned int width=height*RADIX_TREE_MAP_SHlFT; // RADIX_TREE_MAP_SHlFT值为6时,表示每个结点有2^6=64个slot,值为4时,表示有2^4=16个slot
int shift=RADlX_TREE_INDEX_BlTS-width:
if(shift<0)
return ~0UL;
if(shift>=BITS_PER_LONG)
return 0UL;
return~0UL>>shift;
}
先由高度(树的层数)和每节点的索引位宽(RADIX_TREE_MAP_SHlFT用几位做索引)得到总索引的位宽width,再由位宽转化为最大索引(即叶子的个数),比如32位的索引的最大值是2^32-1,4位双层树的最大索引是2^(2*4)-1。(4位数做索引,每个节点可以有2^4=16个分支(slot),那么第二层共有2^(2*4)个节点,从第二层最左端开始编号,最大索引为2^(2*4)-1)。通过循环调用这个函数可以得到各种高度的树的最大索引值存放在一个静态数组height_to_maxindex中。这是在初始化期间调用radix_tree_init()->radix_tree_init_maxindex()实现的。
(2) 对象的插入
参数root指向根节点,index指示页索引,item:
int radix_tree_insert (struct radix_tree_root *root,unsigned long index,void *item)
{
struct radix_tree_node*node=NULL,*sIot;
unsigned int height,shift;
int offset;
int error;
BUG_0N(radix_tree_is_indirect_ptr(item));
//如果当前索引超出树的最大索引,必须调用radix_tree_extend()扩充树的高度直至最大索引可容纳参数中的索引值
if (index>radix_tree_maxindex(root->height)){
error=radix_tree_extend(root,index);
if(error)
return error;
)
sIot=radix_tree_indirect_to_ptr(root->rnode);
//取当前树的高度he-ght,以及页索引的初始右移位数shift
height=root->height;
shift=(height-1)*RADIX_TREE_MAP_SHIFT;
offset=0; /*uninitiaIised var warning*/
//按照索引循环从height层往下检索,直到第1层节点为止(中间按需分配子树结点)
whiIe(height>0){
//遇到sIot为空指针,则需要分配中间节点
if(sIot==NULL){
/*Have to add a chiId node.*/
if(!(slot=radjx_tree_node_alloc(root)))//调用SIab分配器分配新的节点
return –ENOMEM;
slot->height=height;//设置节点高度
//node非空,则新分配节点作为其子节点,否则新分配节点作为根节点
if(node){
//新分配节点指针放入node的指针数组中的offset槽位
rcu_assign_pointer(node->sIots[offset],sJot);
node->count++;∥node的孩子节点数增1
}else
rcu_assign_pointer(root->rnode,radix_tree_ptr_to_indirect(sIot));
}
//调整索引,node、sIot向下走(sIot指向node的子节点),调整移位数,高度减1
offset=(index>>shift)&RADIX_TREE_MAP_MASK;// 根据数据项索引,计算当前层数据项应该的槽位,如索引为32位,采用4位做key,则该数据项在最顶层所在槽位即为前四位对应的槽位,第二层(从上到下)所对应的槽位为接下来4位对应的槽位
node=sIot;
sIot=node->sIots[offset];
shift-=RADIX_TREE_MAP_SHIFT;
height--;
)
/*第1层节点node的位索引。什set对应的槽位(数组项)指向item指示的对象,从而完成了对象的插入*/
if(node){
node->count++;
rcu_assign_pointer(node->sIots[offset],item);
…
}
(3) 对象的删除:
void *radi×_tree_deIete(struct radix_tree_root *root,unsignedIong index)
{
/*使用path数组存放搜索路径沿途的节点指针和索引,数组长度为最大路径长度(数的最大高度)+1,多出来的一项存放空指针(起哨兵作用)*/
struct radix_tree_path path[RADIX_TREE_MAX_PATH+1],*pathp=path;
struct radix_tree_node *slot=NULL;
struct radix_tree_node *to_free;
unsjgned int height,shift;
int tag;
int offset;
//height初始化为树的高度
height=root->height:
//检查待删除对象的索引是否超出树的范围
if(index>radix_tree_maxindex(height))
goto out;
//sIot初始化指向根节点,在以下过程中slot始终指向一个中间节点
sIot=root->rnode;
//对于高度为0的空树直接返回
if(height==0){
root_tag_clear_all(root);
root->rnode=NULL:
goto out;
}
slot=radix_tree_indirect_to_ptr(sIot);
//shift中保存索引当前需要移位的位数
shift=(height-1)*RADIX_TREE_MAP_SHIFT;
//path数组第0项的node置为空,作为指示哨用
pathp->node=NULL;
//这个循环自根节点向下遍历id对应的对象,沿途节点和槽位存于pathp指向的数组中
do{
if(sIot==NULL)//途中遇到空指针(指定对象肯定不存在),直接返回
goto out;
pathp++; //径数组指针递增pathp->node存放当前节点的槽索引,pathp->node存放当前节点
offset=(index>>shift)&RADIX_TREE_MAP_MASK;
pathp->offset=offset;
pathp->node=sIot;
//根据索引获取下一个节点的指针,并调整移位数
sIot=slot->sIots[offset];
shift-=RADIX_TREE_MAP_SHIFT;
height--;
} whiIe(height>0);
if(sIot==NULL)
goto out;
...
to_free=NULL;
/*这个循环借助pathp数组的记录,从待删除对象的父节点沿途至根节点的方向进行遍历,对应的槽位指针置空(底层节点槽位指针置空即从树中删除了对象),子节点数递减,释放槽位全空的节点。两种情况下循环终止:(1)已到达并处理完根节点(2)碰到了子节点数不为0的节点*/
while(pathp->node){
pathp->node->sIots[pathp->offset]=NULL;
pathp->node->count--;
/*Queue the node for deferred freeina after the last reference to it disappears(set NULL,above)*/
if(to_free)
radix_tree_node_free(to_free);
//碰到了子节点数不为0的节点,如果是根节点,调用radix-tree_shrink()尝试收缩树,然后退出循环
if(pathp->node->count){
if(pathp->node==radix_tree_indirect_to_ptr(root->rnode))
radix_tree_shrink(root);
goto out;
}
//Node with zero slots in use so free it
to_free=pathp->node;
pathp--;
}
/*运行到此处表明树不包含对象成为空树,释放掉to_free包含的根节点,树高置为0,根指针置空*/
root_tag_clear_aIl(root);
root->height=0;
root->rnode=NULL;
if(to_free)
radix_tree_node_free(to_free);
out:
return sIot;
}
(4)树的扩展:
statIc int radix_tree_extend (struct radix_tree_root *root,unsigned Iong index)
{
struct radix_tree_node *node;
unsigned int height;
int tag;
//高度增1
height=root->height+1;
∥循环比较树的最大索引值和index.通过递增高度最终使树能够容纳指定索引的对象
while(index>radix_tree_maxindex(height))
height++;
//对于空树,留待以后分配节点,这里仅调整树的高度
if(root->rnode==NULL){
root->height=height;
goto out;
}
通过在原根节点以上增加一段单支子树.从而使树高达到指定值,根节点被新增子树的根取代,新增子树的叶子节点指向原根/节点,新增的节点具有除槽位0的指针指向子节点外其余槽位都是空指针,也就是最左单支树的特征.这种调整相当于在原id位串的高位增加了一串0,从而使原对象id值和其在新扩树中的位置仍保持正确的对应关系。
do{
unsigned int newheight;
if(! (node=radix_tree_node_aIIoc(root)))
return -ENOMEM;
/*lncrease the height.*/
node->slots[0]=radix_tree_indirect_to_ptr(root->rnode);
/*Propagate the aggregated tag info into the new root*/
for(tag=0;tag<RADIX_TREE_MAX_TAGS;tag++){
if(root_tag_get(root,tag))
tag_set(node,tag,0);
}
newheight=root->height+1;
node->height=newheight;
node->count=1;
node=radix_tree_ptr_to_indirect(node);
rcu_assign_pointer(root->rnode,node);
root->height=newheight;
}whiIe(height>root->height):
out:
return 0;
}
(5) 树的收缩。
从根节点开始向下检查符合除第0个槽位外其他槽位指针都空的条件的节点,直至遇到第n层的节点不满足这个条件,把1~n-1层的单支树收缩,释放沿途节点f返还给slab分配器),然后把n层节点作为新的根节点:
static inIine void radix_tree_shrink (struct radix_tree_root *root)
{
/*try to shrink tree height*/
whiIe(root->height>0){
struct radix_tree_ node *to_ free=root->rnode;
void* newptr;
BUG_0N(!radix_free_is_indirect_ptr(to_free));
to_free=radix_tree_indirect_to_ptr(to_free);
//当前节点子节点数不等于1则退出循环
if(to_free->count!=1)
break;
//子节点不是第0槽位的指针指向也退出循环
if(!to_free->slots[0])
break;
//newptr存放to_free的唯一的子节点指针
newptr=to_free->slots[0];
if(root->height>1)
newptr=radix_free_ptr_to_indirect(newptr);
//子节点作为新的根节点
root->rnode=newptr;
root->height--;//树的高度递减
/*must only free zeroed nodes into the sIab*/
tag_clear(to_free,0,0);
tag_cIear(to_free,1,0);
∥释放to_free节点
to_free->sIots[0]=NULL;
to_free->count=0;
radix_tree_node_free(to_free);
}
}
(6)根据页索引index查询对象:
void *radix_tree_Iookup (struct radix_tree_root *root, unsigned long index)
{
unsigned int height,shift;
struct radix_tree_node *node,**slot;
node=rcu_dereference(root->rnode);
…
height=node->height;
if(index>radix_tree_maxindex(height))
return NULL;
//设置初始移位的位数
shlft=(height-1)*RADIX_TREE_MAP_SHlFT;
/*从顶向下循环逐层检索,先由index、移位数shift和位掩码获取槽索引,再由当前节点node和槽索引获取槽位sIot.然后node指向节点指针槽指示的下层节点,最后重新调整移位数shift和当前高度height,直至到达0层,此时node即指向了对象*/
do{
sIot=(struct radix_tree_node**)(node->sIots+((index>>shift)&RADIX_TREE_MAP_MASK));
node=rcu_dereference(*sIot);
if(node==NULL)
return NULL;
shift-=RADIX_TREE_MAP_SHlFT;
height--;
}whiIe(height>0);
return node;
}
2.2 Linux\Iib\idr.c
idr机制基本上也是基数树的一套方法.但是它又多了寻找空闲id的功能,所以不能完全照搬上面的机制。
具体代码分析略。
3. 外围函数
3.1文件页缓存
add_to_page_cache()函数调用radix_tree_insert()把指定页插入指定的文件页缓存基数树的指定位置,find_get_page()在地址空间的基数树中寻找指定索引的页。这两个函数都包含于Linux\mm\filemap.c。它们对基数树的动作分别是写和读,由于radix_tree.c中的基数树的函数本身没有同步手段,因此要求调用它们的外围函数包含同步措施.而这两个外围函数使用了地址空间的读写锁,add_to_page_cache()在调用radix_tree_insert()前先调用write_lock_irq(&mapping->tree_lock);进行了写锁定,而find_get_page()则调用read_lock_irq(&mapping->tree_lock);进行读锁定。
3.2 ipc的idr机制
ipc_findkey()调用idr_find()由0开始遍历基数树,直至找到指定键值的对象;ipc_addid()调用idr_get_new()将对象加入idr树并返回和位置对应的id;ipc_rmid()调用idr_remove()从idr树删除指定id的对象,这些函数包含于Linux\ipc\unic.c。它们的同步问题则由最外层的ipc函数使用读写信号量保证,比如ipc_rmid()的调用路径为shm_close()->shm_destroy()->shm_rmid()->ipc_rmid(), shm_close()中使用down_write(&shm_ids (ns).r_—mutex);把共享内存的ids给锁住了,这样牺牲了一定的并发性,但保证了数据的一致性.以后的版本估计会使用更细粒度的锁或并发性更好的机制。同理,ipc_addid()的调用路径为sys_shmget()->ipcget()->ipcget_new()->newseg()->shm_addid()->ipc_addid(),在ipcget_new()中也使用down_write(&ids->rw_mutex);写锁定了整个ids。
5 .结语
对于根据id定位对象的数据结构,固定数组最直接,速度最快。而以逻辑运算加移位
操作的组合作为散列函数的散列表则次之。但是数组适用于对象数变化不大或者最大对象数不是很多的场合,非常不适于对象分布稀疏的场合,否则内存的浪费比较严重;而散列表在查询和插入删除时要求锁住整个表,对于共享频繁的场合会导致并发性能不佳,此外由于缺少数组那样的位置和id的映射唯一性,从而不适用于需要自动生成id的场合。基数树则取长补短,它的搜索性能在可接受范围内,内存消耗也不大,又具有动态性,能按需收缩或者扩充。更重要的是它和数组一样具有位置和id的唯一映射关系,从而很容易在加入新对象的同时生成id值,这是散列表所没有的.此外系统中可以创建很多这样的树,因此也提高了并发性能。
原文地址:http://blog.chinaunix.net/uid-28541347-id-5018036.html