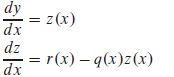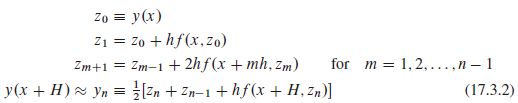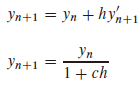[摘记]数值方法12——常微分方程组的积分
注:以下来自《C++数值算法一书》,仅对章节内容做摘要,为的是给自己扫盲,不涉及算法。
与常微分方程组ODE有关的问题常常都可以化为一系列一阶微分方程的问题来研究。
可化为两个一阶微分方程
常微分方程组的解不完全由其方程决定,要确定方程的解还需要边界值条件。边界值条件分为初值问题和两点边值问题,本章主要讨论初值问题。
1. 龙格库塔法Runge-Kutta
通过类似于欧拉方法中的步长(每次都要算出右边的f值),把各个步长所提供的信息结合起来,算出有一定间隔的值解,然后利用所有信息和泰勒展开式匹配,以得到高阶近似解。
工程上常用的是四阶龙格库塔法。
2. Runge-Kutta法的自适应步长控制
自适应步长的控制是为了用尽可能少的计算量达到解的预定精确度。在一些不可靠的地方,应该用一些较小的步长,在一些平滑的无关紧要的地方,则用大一些的步长以加快计算过程。对于四阶Rungge-Kutta法,最直接的方法是步长数加倍,而对五阶方法,更有效的是Cash-Karp Runge-Kutta法。
3. 修正中点法
从点x到点x+H,通过每一步长为h的n=H/h子步来计算因变量y(x)向量。
4. Richardson外推法和Bulirsch-Stoer方法
Richardson外推法利用了一种很有效的思想,它是在如果步长比实际值小得多时,对能得到的计算值进行外推。特殊情况下,趋近于0的步长值进行外推是理想的目标,Bulirsch和Stoer首次把这种方法应用到常微分方程的积分中,因此外推法常被称为Bulirsch-Stoer方法。
在两种情况下,用自适应步长的Runge-Kutta法会有更好的效果,一是方程右边的函数值是通过查找表或插值来定义的;或者微分方程的积分区间中有奇异点。
除了上面两个缺点外,Bulirsch-Stoer方法是用最小的计算达到常微分方程求解高精度的一个目前来说最好的方法。一个大的间隔H由逐渐细分的子步序列来组成。其结果是对设想的无穷细分的子步进行外推,积分法采用修正中点法,外推法是采用有理函数或多项式的外推法。
5. 刚性方程组
刚性问题通常出现在自变量的取值有两个或多个不同尺度,而因变量正随此而变化的问题中。刚性方程需要在解的取值较小的度量范围内变化步长,以保持积分的稳定性,尽管积分精度可以允许一个比较大的步长。
对于![]() ,c>0是一个常数,使用显式(向前)欧拉公式,得到: (书上错了,向前欧拉是显式方法,向后欧拉是隐式方法)
,c>0是一个常数,使用显式(向前)欧拉公式,得到: (书上错了,向前欧拉是显式方法,向后欧拉是隐式方法)
在h>2/c的情况下,就无法得到收敛的y值。遇到这样的问题,解决的方法便是使用隐式差分,使用向后欧拉格式:
当h->∞时,仍有yn+1->0。
但并非所有的方程都是常系数的线性方程,我们必须每步进行迭代处理,用线性化解决隐式解法的问题,称为半隐式解法。这种解法通常是稳定的。
目前刚性方程组三种重要的高阶算法有:通用的Runge-Kutta方法,其中最有用的是Rosenbrock方法。首次用这个思想进行实践的是Kaps等,因此又被称为Kaps-Rentrop方法;通用的Bulirsch-Stoer方法,尤其是Bader和Deuflhard提出的半隐式外推方法;预测校正法,其主要部分是Gear后向差分法的继续。
6. 多步法、多值法和预测-校正法
略
这一章因为之前在做服装模拟,关于怎么解ODE,试了一些方法,显示的、半隐式的,龙格库塔、共轭梯度、Verlet 积分之类的。
其实这些方法都不会出现在这本书的同一章了,我至今仍有些混乱,不知道什么样的问题该用什么方法。很多方法都明白了,但看书时仍觉得很吃力。我觉得这本书的语言并不够明了,总试图绕着圈子高深地去解释一种方法,有时候WIKI能得到更好的答案。而且也有些错误,比如我看到隐式的向前欧拉就一阵混乱。还是做一个总结,到要用的时候,就去google之吧。
本文原创,转载请注明出处