torch.nn中的非线性激活使用

1、神经网络中的非线性激活

  在神经网络中，**非线性激活函数（Non-linear Activation Functions）**是引入非线性变换的关键组件，使神经网络能够学习并建模复杂的非线性关系。如果没有激活函数，无论神经网络有多少层，其整体表现仍等同于一个线性模型（如逻辑回归），无法解决非线性问题（如图像分类、自然语言处理等）。

为什么需要非线性激活？

• 打破线性限制：线性变换的叠加仍然是线性的（如矩阵乘法的结合律）。非线性激活允许网络学习输入数据中的非线性模式。
• 增强表达能力：通过非线性激活，神经网络可以逼近任意复杂函数（万能逼近定理）。
• 多层级联的有效性：深层网络的每一层通过非线性激活逐步提取更高阶的特征（如边缘→纹理→物体部件→完整物体）。

常见非线性激活函数

1. Sigmoid
   公式：$$\sigma (x)=\frac{1}{1+e^{-x}}$$
   输出范围：(0, 1)
   用途：二分类输出层（概率输出）。
   缺点：
   梯度消失（梯度在两端接近0，深层网络难以训练）。
   输出非零中心（可能影响梯度下降效率）。

2. Tanh（双曲正切）
   公式：$$\tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
   输出范围：(-1, 1)
   优点：零中心化（缓解梯度下降的震荡问题）。
   缺点：梯度消失问题仍存在。

3. ReLU（Rectified Linear Unit）
   公式：$$\text{ReLU}(x)=\max (0,x)$$
   优点：
   计算高效（无需指数运算）。
   缓解梯度消失（正区间梯度恒为1）。
   缺点：
   Dead ReLU问题：负输入梯度为0，神经元可能永久失效（可通过Leaky ReLU或初始化优化缓解）。

4. Leaky ReLU
   公式：$$\text{LeakyReLU}(x)=\{\begin{array}{ll}x& \text{if }x\ge 0\\ \alpha x& \text{if }x<0\end{array}$$
   改进：负区间引入小斜率（如α=0.01），避免神经元死亡。

5. Swish
   公式：$$\text{Swish}(x)=x\cdot \sigma (\beta x)$$（σ为Sigmoid，β可学习或固定）
   特点：平滑且非单调，在某些任务中表现优于ReLU。

6. Softmax
   公式：对输出层进行归一化，$$\text{Softmax}(x_i)=\frac{e^{x_i}}{{\sum }_j{e}^{x_j}}$$
   用途：多分类输出层，输出概率分布。

如何选择激活函数？

• 隐藏层：通常首选 ReLU（简单高效），深层网络可尝试 Leaky ReLU 或 Swish。
• 输出层：
  二分类：Sigmoid。
  多分类：Softmax。
  回归问题：线性激活（无激活函数）。

非线性激活的作用示例
假设一个简单的神经网络：

无激活函数：
$$\text{Output}=W_2(W_{1}X+b_1)+b_2=(W_2{W}_1)X+(W_2{b}_1+b_2)$$
等价于单层线性模型。

加入ReLU：
$$\text{Output}=W_2\cdot \text{ReLU}(W_{1}X+b_1)+b_2$$
非线性关系得以保留，模型能力显著提升。

总结
  非线性激活函数是神经网络的核心，决定了模型的表达能力和训练动态。选择时需权衡梯度传播效率、计算成本和任务需求。现代深度学习框架（如PyTorch、TensorFlow）已内置多种激活函数，开发者可通过实验选择最佳方案。

2、torch.nn中的非线性激活

Non-linear Activations
使用方法见：torch.nn中的非线性激活介绍合集——Pytorch中的非线性激活

• nn.ELU——按元素应用 Exponential Linear Unit （ELU） 函数。
• nn.Hardshrink——按元素应用 Hard Shrinkage （Hardshrink） 函数。
• nn.Hardsigmoid——按元素应用 Hardsigmoid 函数。
• nn.Hardtanh——按元素应用 HardTanh 函数。
• nn.Hardswish——按元素应用 Hardswish 函数。
• nn.LeakyReLU——按元素应用 LeakyReLU 函数。
• nn.LogSigmoid——按元素应用 Logsigmoid 函数。
• nn.MultiheadAttention——允许模型共同关注来自不同表示子空间的信息。
• nn.PReLU——应用元素级 PReLU 函数。
• nn.ReLU——按元素应用修正的线性单元函数。
• nn.ReLU6——按元素应用 ReLU6 函数。
• nn.RReLU——按元素应用随机泄漏整流线性单元函数。
• nn.SELU——按元素应用 SELU 函数。
• nn.CELU——按元素应用 CELU 函数。
• nn.GELU——应用 Gaussian Error Linear Units 功能。
• nn.Sigmoid——按元素应用 Sigmoid 函数。
• nn.SiLU——按元素应用 Sigmoid 线性单元 （SiLU） 功能。
• nn.Mish——按元素应用 Mish 函数。
• nn.Softplus——按元素应用 Softplus 函数。
• nn.Softshrink——按元素应用软收缩功能。
• nn.Softsign——应用元素级 Softsign 函数。
• nn.Tanh——按元素应用 Hyperbolic Tangent （Tanh） 函数。
• nn.Tanhshrink——应用元素级 Tanhshrink 函数。
• nn.Threshold——对输入 Tensor 的每个元素进行阈值设置。
• nn.GLU——应用门控线性单元功能。

3、torch.nn中非线性激活的使用实例

3.1 nn.ReLU使用实例

import torch
from torch import nn
from torch.nn import ReLU

input = torch.tensor([[3, -2],
                      [1, -1.5]])
print(input.shape)

class My_module(nn.Module):
    def __init__(self):
        super(My_module, self).__init__()
        self.relu1 = ReLU()  

    def forward(self, input):
        output = self.relu1(input)
        return output

mymodule = My_module()
output = mymodule(input)
print(output)                    

输出：

torch.Size([2, 2])
tensor([[3., 0.],
        [1., 0.]])

可以看到，原始输入中小于0的元素都被整流为0了，大于等于0的元素保持不变。

3.2 nn.Sigmoid使用实例

1. 测试nn.Sigmoid

import torch
from torch import nn
from torch.nn import Sigmoid

input = torch.tensor([1, 0])

print(input.shape)

class My_module(nn.Module):
    def __init__(self):
        super(My_module, self).__init__()
        self.sigmoid1 = Sigmoid()

    def forward(self, input):
        output = self.sigmoid1(input)
        return output

mymodule = My_module()
output = mymodule(input)
print(output)

torch.Size([2])
tensor([0.7311, 0.5000])

可以代入数据验证一下：$$\sigma (x)=\frac{1}{1+e^{-x}}$$

$$\sigma (1)=\mathrm{0.7310585786...}$$$$\sigma (0)=0.5000$$

2. 使用真实图像数据
   使用torchvision.datasets内置数据集并使用torchvision.transforms预处理数据集，使用DataLoader加载数据。
   torchvision.datasets内置数据集、transforms、DataLoader及Tensorboard的使用见：
   torchvision中数据集的使用
   Pytorch中的Transforms学习
   Pytorch中DataLoader的介绍
   Pytorch中Tensorboard的学习

import torch
import torchvision
from torch import nn
from torch.nn import Sigmoid
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter


dataset = torchvision.datasets.CIFAR10("dataset", train=False, download=False,
                                       transform=torchvision.transforms.ToTensor())

dataloader = DataLoader(dataset, batch_size=32)

class My_module(nn.Module):
    def __init__(self):
        super(My_module, self).__init__()
        self.sigmoid1 = Sigmoid()

    def forward(self, input):
        output = self.sigmoid1(input)
        return output

mymodule = My_module()

writer = SummaryWriter("runs")
step = 0
for data in dataloader:
    imgs, targets = data
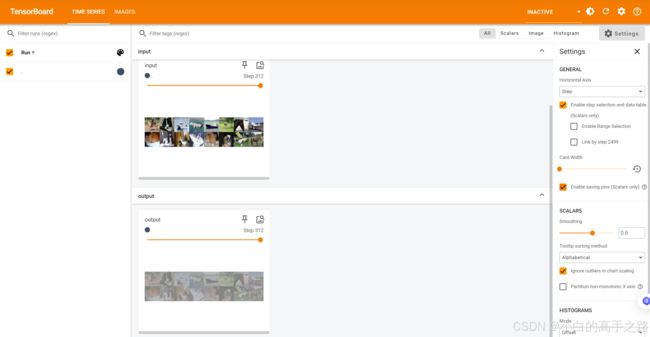
    writer.add_images("input", imgs, global_step=step)
    output = mymodule(imgs)
    writer.add_images("output", output, step)
    step += 1

writer.close()

运行完在终端执行命令：

tensorboard --logdir=runs

TensorFlow installation not found - running with reduced feature set.
Serving TensorBoard on localhost; to expose to the network, use a proxy or pass --bind_all
TensorBoard 2.19.0 at http://localhost:6006/ (Press CTRL+C to quit)

打开网址：