POJ 3608 Bridge Across Islands(计算几何の旋转卡壳)
Description
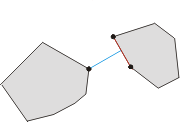
Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.
Input
The input consists of several test cases.
Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000)
Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon.
Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon.
A line with N = M = 0 indicates the end of input.
The coordinates are within the range [-10000, 10000].
Output
For each test case output the minimal distance. An error within 0.001 is acceptable.
题目大意:给两个凸多边形,求两个凸多边形的最近距离
思路:用旋转卡壳,最短距离一定在两条支撑线之间(相当于切线吧大概……),详见代码,表达能力渣渣
PS:此题虽然没说点的顺序,DISCUSS里面有人说是乱序的,但实际上好像是逆序的(反正我不考虑点的顺序也能过就是了……)
代码(125MS):

1 #include <cstdio> 2 #include <cstring> 3 #include <cmath> 4 #include <algorithm> 5 using namespace std; 6 7 #define EPS 1e-8 8 #define MAXN 10010 9 10 inline int sgn(double x) { 11 if(fabs(x) < EPS) return 0; 12 return x > 0 ? 1 : -1; 13 } 14 15 struct Point { 16 double x, y; 17 Point(double xx = 0, double yy = 0): x(xx), y(yy) {} 18 }; 19 //cross 20 inline double operator ^ (const Point &a, const Point &b) { 21 return a.x * b.y - a.y * b.x; 22 } 23 24 inline double operator * (const Point &a, const Point &b) { 25 return a.x * b.x + a.y * b.y; 26 } 27 28 inline Point operator - (const Point &a, const Point &b) { 29 return Point(a.x - b.x, a.y - b.y); 30 } 31 32 inline double dist(const Point &a, const Point &b) { 33 return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); 34 } 35 36 inline double Cross(Point o, Point s, Point e) { 37 return (s - o) ^ (e - o); 38 } 39 40 struct Line { 41 Point s, e; 42 Line() {} 43 Line(Point ss, Point ee): s(ss), e(ee) {} 44 }; 45 46 inline double Point_to_Line(const Point &p, const Line &L) { 47 return fabs(Cross(p, L.s, L.e)/dist(L.s, L.e)); 48 } 49 50 inline double Point_to_Seg(const Point &p, const Line &L) { 51 if(sgn((L.e - L.s) * (p - L.s)) < 0) return dist(p, L.s); 52 if(sgn((L.s - L.e) * (p - L.e)) < 0) return dist(p, L.e); 53 return Point_to_Line(p, L); 54 } 55 56 inline double Seg_to_Seg(const Line &a, const Line &b) { 57 double ans1 = min(Point_to_Seg(a.s, b), Point_to_Seg(a.e, b)); 58 double ans2 = min(Point_to_Seg(b.s, a), Point_to_Seg(b.e, a)); 59 return min(ans1, ans2); 60 } 61 62 inline double solve(Point *p, Point *q, int np, int nq) { 63 p[np] = p[0]; 64 q[nq] = q[0]; 65 int sp = 0, sq = 0; 66 for(int i = 0; i < np; ++i) if(sgn(p[i].y - p[sp].y) < 0) sp = i; 67 for(int i = 0; i < nq; ++i) if(sgn(q[i].y - q[sq].y) < 0) sq = i; 68 double tmp, ans = dist(p[0], q[0]); 69 for(int i = 0; i < np; ++i) { 70 while(sgn(tmp = (Cross(q[sq], p[sp], p[sp+1]) - Cross(q[sq+1],p[sp],p[sp+1]))) < 0) 71 sq = (sq + 1) % nq; 72 if(sgn(tmp) > 0) 73 ans = min(ans, Point_to_Seg(q[sq], Line(p[sp], p[sp+1]))); 74 else 75 ans = min(ans, Seg_to_Seg(Line(p[sp], p[sp+1]), Line(q[sq], q[sq+1]))); 76 sp = (sp + 1) % np; 77 } 78 return ans; 79 } 80 81 Point p[MAXN], q[MAXN]; 82 int np, nq; 83 84 int main() { 85 while(scanf("%d%d", &np, &nq) != EOF) { 86 if(np == 0 && nq == 0) break; 87 for(int i = 0; i < np; ++i) 88 scanf("%lf%lf", &p[i].x, &p[i].y); 89 for(int i = 0; i < nq; ++i) 90 scanf("%lf%lf", &q[i].x, &q[i].y); 91 printf("%f\n", min(solve(p, q, np, nq), solve(q, p, nq, np))); 92 } 93 return 0; 94 }
代码(141MS)(高度模板化):

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 #include <cmath> 6 using namespace std; 7 8 const int MAXN = 10010; 9 const double EPS = 1e-10; 10 const double PI = acos(-1.0);//3.14159265358979323846 11 const double INF = 1; 12 13 inline int sgn(double x) { 14 return (x > EPS) - (x < -EPS); 15 } 16 17 struct Point { 18 double x, y, ag; 19 Point() {} 20 Point(double x, double y): x(x), y(y) {} 21 void read() { 22 scanf("%lf%lf", &x, &y); 23 } 24 bool operator == (const Point &rhs) const { 25 return sgn(x - rhs.x) == 0 && sgn(y - rhs.y) == 0; 26 } 27 bool operator < (const Point &rhs) const { 28 if(y != rhs.y) return y < rhs.y; 29 return x < rhs.x; 30 } 31 Point operator + (const Point &rhs) const { 32 return Point(x + rhs.x, y + rhs.y); 33 } 34 Point operator - (const Point &rhs) const { 35 return Point(x - rhs.x, y - rhs.y); 36 } 37 Point operator * (const double &b) const { 38 return Point(x * b, y * b); 39 } 40 Point operator / (const double &b) const { 41 return Point(x / b, y / b); 42 } 43 double operator * (const Point &rhs) const { 44 return x * rhs.x + y * rhs.y; 45 } 46 double length() { 47 return sqrt(x * x + y * y); 48 } 49 Point unit() { 50 return *this / length(); 51 } 52 void makeAg() { 53 ag = atan2(y, x); 54 } 55 void print() { 56 printf("%.10f %.10f\n", x, y); 57 } 58 }; 59 typedef Point Vector; 60 61 double dist(const Point &a, const Point &b) { 62 return (a - b).length(); 63 } 64 65 double cross(const Point &a, const Point &b) { 66 return a.x * b.y - a.y * b.x; 67 } 68 //ret >= 0 means turn right 69 double cross(const Point &sp, const Point &ed, const Point &op) { 70 return cross(sp - op, ed - op); 71 } 72 73 double area(const Point& a, const Point &b, const Point &c) { 74 return fabs(cross(a - c, b - c)) / 2; 75 } 76 //counter-clockwise 77 Point rotate(const Point &p, double angle, const Point &o = Point(0, 0)) { 78 Point t = p - o; 79 double x = t.x * cos(angle) - t.y * sin(angle); 80 double y = t.y * cos(angle) + t.x * sin(angle); 81 return Point(x, y) + o; 82 } 83 84 struct Seg { 85 Point st, ed; 86 double ag; 87 Seg() {} 88 Seg(Point st, Point ed): st(st), ed(ed) {} 89 void read() { 90 st.read(); ed.read(); 91 } 92 void makeAg() { 93 ag = atan2(ed.y - st.y, ed.x - st.x); 94 } 95 }; 96 typedef Seg Line; 97 98 //ax + by + c > 0 99 Line buildLine(double a, double b, double c) { 100 if(sgn(a) == 0 && sgn(b) == 0) return Line(Point(sgn(c) > 0 ? -1 : 1, INF), Point(0, INF)); 101 if(sgn(a) == 0) return Line(Point(sgn(b), -c/b), Point(0, -c/b)); 102 if(sgn(b) == 0) return Line(Point(-c/a, 0), Point(-c/a, sgn(a))); 103 if(b < 0) return Line(Point(0, -c/b), Point(1, -(a + c) / b)); 104 else return Line(Point(1, -(a + c) / b), Point(0, -c/b)); 105 } 106 107 void moveRight(Line &v, double r) { 108 double dx = v.ed.x - v.st.x, dy = v.ed.y - v.st.y; 109 dx = dx / dist(v.st, v.ed) * r; 110 dy = dy / dist(v.st, v.ed) * r; 111 v.st.x += dy; v.ed.x += dy; 112 v.st.y -= dx; v.ed.y -= dx; 113 } 114 115 bool isOnSeg(const Seg &s, const Point &p) { 116 return (p == s.st || p == s.ed) || 117 (((p.x - s.st.x) * (p.x - s.ed.x) < 0 || 118 (p.y - s.st.y) * (p.y - s.ed.y) < 0) && 119 sgn(cross(s.ed, p, s.st) == 0)); 120 } 121 122 bool isIntersected(const Point &s1, const Point &e1, const Point &s2, const Point &e2) { 123 return (max(s1.x, e1.x) >= min(s2.x, e2.x)) && 124 (max(s2.x, e2.x) >= min(s1.x, e1.x)) && 125 (max(s1.y, e1.y) >= min(s2.y, e2.y)) && 126 (max(s2.y, e2.y) >= min(s1.y, e1.y)) && 127 (cross(s2, e1, s1) * cross(e1, e2, s1) >= 0) && 128 (cross(s1, e2, s2) * cross(e2, e1, s2) >= 0); 129 } 130 131 bool isIntersected(const Seg &a, const Seg &b) { 132 return isIntersected(a.st, a.ed, b.st, b.ed); 133 } 134 135 bool isParallel(const Seg &a, const Seg &b) { 136 return sgn(cross(a.ed - a.st, b.ed - b.st)) == 0; 137 } 138 139 //return Ax + By + C =0 's A, B, C 140 void Coefficient(const Line &L, double &A, double &B, double &C) { 141 A = L.ed.y - L.st.y; 142 B = L.st.x - L.ed.x; 143 C = L.ed.x * L.st.y - L.st.x * L.ed.y; 144 } 145 //point of intersection 146 Point operator * (const Line &a, const Line &b) { 147 double A1, B1, C1; 148 double A2, B2, C2; 149 Coefficient(a, A1, B1, C1); 150 Coefficient(b, A2, B2, C2); 151 Point I; 152 I.x = - (B2 * C1 - B1 * C2) / (A1 * B2 - A2 * B1); 153 I.y = (A2 * C1 - A1 * C2) / (A1 * B2 - A2 * B1); 154 return I; 155 } 156 157 bool isEqual(const Line &a, const Line &b) { 158 double A1, B1, C1; 159 double A2, B2, C2; 160 Coefficient(a, A1, B1, C1); 161 Coefficient(b, A2, B2, C2); 162 return sgn(A1 * B2 - A2 * B1) == 0 && sgn(A1 * C2 - A2 * C1) == 0 && sgn(B1 * C2 - B2 * C1) == 0; 163 } 164 165 double Point_to_Line(const Point &p, const Line &L) { 166 return fabs(cross(p, L.st, L.ed)/dist(L.st, L.ed)); 167 } 168 169 double Point_to_Seg(const Point &p, const Seg &L) { 170 if(sgn((L.ed - L.st) * (p - L.st)) < 0) return dist(p, L.st); 171 if(sgn((L.st - L.ed) * (p - L.ed)) < 0) return dist(p, L.ed); 172 return Point_to_Line(p, L); 173 } 174 175 double Seg_to_Seg(const Seg &a, const Seg &b) { 176 double ans1 = min(Point_to_Seg(a.st, b), Point_to_Seg(a.ed, b)); 177 double ans2 = min(Point_to_Seg(b.st, a), Point_to_Seg(b.ed, a)); 178 return min(ans1, ans2); 179 } 180 181 struct Poly { 182 int n; 183 Point p[MAXN];//p[n] = p[0] 184 void init(Point *pp, int nn) { 185 n = nn; 186 for(int i = 0; i < n; ++i) p[i] = pp[i]; 187 p[n] = p[0]; 188 } 189 double area() { 190 if(n < 3) return 0; 191 double s = p[0].y * (p[n - 1].x - p[1].x); 192 for(int i = 1; i < n; ++i) 193 s += p[i].y * (p[i - 1].x - p[i + 1].x); 194 return s / 2; 195 } 196 }; 197 //the convex hull is clockwise 198 void Graham_scan(Point *p, int n, int *stk, int &top) {//stk[0] = stk[top] 199 sort(p, p + n); 200 top = 1; 201 stk[0] = 0; stk[1] = 1; 202 for(int i = 2; i < n; ++i) { 203 while(top && cross(p[i], p[stk[top]], p[stk[top - 1]]) <= 0) --top; 204 stk[++top] = i; 205 } 206 int len = top; 207 stk[++top] = n - 2; 208 for(int i = n - 3; i >= 0; --i) { 209 while(top != len && cross(p[i], p[stk[top]], p[stk[top - 1]]) <= 0) --top; 210 stk[++top] = i; 211 } 212 } 213 //use for half_planes_cross 214 bool cmpAg(const Line &a, const Line &b) { 215 if(sgn(a.ag - b.ag) == 0) 216 return sgn(cross(b.ed, a.st, b.st)) < 0; 217 return a.ag < b.ag; 218 } 219 //clockwise, plane is on the right 220 bool half_planes_cross(Line *v, int vn, Poly &res, Line *deq) { 221 int i, n; 222 sort(v, v + vn, cmpAg); 223 for(i = n = 1; i < vn; ++i) { 224 if(sgn(v[i].ag - v[i-1].ag) == 0) continue; 225 v[n++] = v[i]; 226 } 227 int head = 0, tail = 1; 228 deq[0] = v[0], deq[1] = v[1]; 229 for(i = 2; i < n; ++i) { 230 if(isParallel(deq[tail - 1], deq[tail]) || isParallel(deq[head], deq[head + 1])) 231 return false; 232 while(head < tail && sgn(cross(v[i].ed, deq[tail - 1] * deq[tail], v[i].st)) > 0) 233 --tail; 234 while(head < tail && sgn(cross(v[i].ed, deq[head] * deq[head + 1], v[i].st)) > 0) 235 ++head; 236 deq[++tail] = v[i]; 237 } 238 while(head < tail && sgn(cross(deq[head].ed, deq[tail - 1] * deq[tail], deq[head].st)) > 0) 239 --tail; 240 while(head < tail && sgn(cross(deq[tail].ed, deq[head] * deq[head + 1], deq[tail].st)) > 0) 241 ++head; 242 if(tail <= head + 1) return false; 243 res.n = 0; 244 for(i = head; i < tail; ++i) 245 res.p[res.n++] = deq[i] * deq[i + 1]; 246 res.p[res.n++] = deq[head] * deq[tail]; 247 res.n = unique(res.p, res.p + res.n) - res.p; 248 res.p[res.n] = res.p[0]; 249 return true; 250 } 251 252 //ix and jx is the points whose distance is return, res.p[n - 1] = res.p[0], res must be clockwise 253 double dia_rotating_calipers(Poly &res, int &ix, int &jx) { 254 double dia = 0; 255 int q = 1; 256 for(int i = 0; i < res.n - 1; ++i) { 257 while(sgn(cross(res.p[i], res.p[q + 1], res.p[i + 1]) - cross(res.p[i], res.p[q], res.p[i + 1])) > 0) 258 q = (q + 1) % (res.n - 1); 259 if(sgn(dist(res.p[i], res.p[q]) - dia) > 0) { 260 dia = dist(res.p[i], res.p[q]); 261 ix = i; jx = q; 262 } 263 if(sgn(dist(res.p[i + 1], res.p[q]) - dia) > 0) { 264 dia = dist(res.p[i + 1], res.p[q]); 265 ix = i + 1; jx = q; 266 } 267 } 268 return dia; 269 } 270 //a and b must be clockwise, find the minimum distance between two convex hull 271 double half_rotating_calipers(Poly &a, Poly &b) { 272 int sa = 0, sb = 0; 273 for(int i = 0; i < a.n; ++i) if(sgn(a.p[i].y - a.p[sa].y) < 0) sa = i; 274 for(int i = 0; i < b.n; ++i) if(sgn(b.p[i].y - b.p[sb].y) < 0) sb = i; 275 double tmp, ans = dist(a.p[0], b.p[0]); 276 for(int i = 0; i < a.n; ++i) { 277 while(sgn(tmp = cross(a.p[sa], a.p[sa + 1], b.p[sb + 1]) - cross(a.p[sa], a.p[sa + 1], b.p[sb])) > 0) 278 sb = (sb + 1) % (b.n - 1); 279 if(sgn(tmp) < 0) ans = min(ans, Point_to_Seg(b.p[sb], Seg(a.p[sa], a.p[sa + 1]))); 280 else ans = min(ans, Seg_to_Seg(Seg(a.p[sa], a.p[sa + 1]), Seg(b.p[sb], b.p[sb + 1]))); 281 sa = (sa + 1) % (a.n - 1); 282 } 283 return ans; 284 } 285 286 double rotating_calipers(Poly &a, Poly &b) { 287 return min(half_rotating_calipers(a, b), half_rotating_calipers(b, a)); 288 } 289 290 /*******************************************************************************************/ 291 292 Poly a, b; 293 294 double solve() { 295 double ans = 1e100; 296 for(int i = 0; i < a.n; ++i) 297 for(int j = 0; j < b.n; ++j) ans = min(ans, dist(a.p[i], b.p[j])); 298 return ans; 299 } 300 301 int main() { 302 while(scanf("%d%d", &a.n, &b.n) != EOF) { 303 if(a.n == 0 && b.n == 0) break; 304 for(int i = 0; i < a.n; ++i) a.p[i].read(); 305 a.p[a.n++] = a.p[0]; 306 for(int i = 0; i < b.n; ++i) b.p[i].read(); 307 b.p[b.n++] = b.p[0]; 308 printf("%f\n", rotating_calipers(a, b)); 309 //printf("%f\n", solve()); 310 } 311 return 0; 312 }
