吴恩达深度学习作业之 PyTorch 实现多分类任务

在这次作业中会学到：（参考 https://zhuanlan.zhihu.com/p/536483424）

• PyTorch与NumPy的相互转换
• PyTorch的常见运算（矩阵乘法、激活函数、误差）
• PyTorch的初始化器
• PyTorch的优化器
• PyTorch维护梯度的方法

数据集

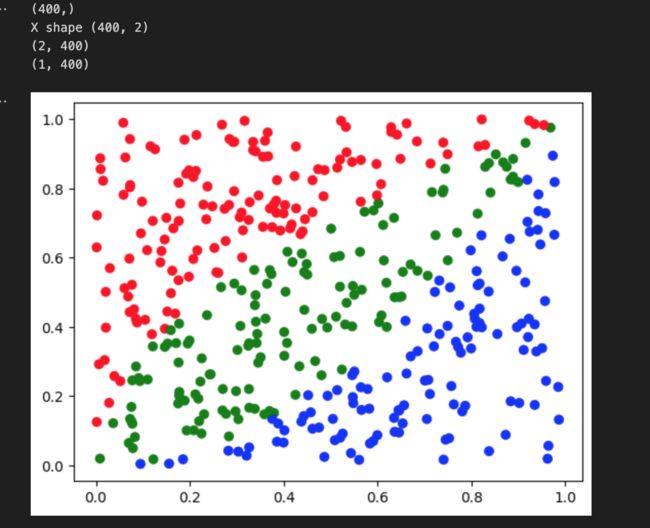
本项目中，我们要用到一个平面点数据集。在平面上，有三种颜色不同的点。我们希望用PyTorch编写的神经网络能够区分这三种点。

import matplotlib.pyplot as plt
import numpy as np
from typing import List

def generate_points(cnt):
    x = np.random.rand(cnt)
    print(x.shape)
    y = np.random.rand(cnt)
    X = np.stack([x,y],1) 

    
    print("X shape", X.shape)
    Y = np.where(y > x * x, np.where(y > x**0.5, 0, 1), 2)
    #np.where(condition, x, y),满足条件(condition)，输出x，不满足输出y。
    # x ** 0.5是x开根号的意思
    return X.T, Y[..., np.newaxis].T
##x[:, np.newaxis] ：放在后面，会给列上增加维度；
##x[np.newaxis, :] ：放在前面，会给行上增加维度；
 
#np.stack 是 NumPy 中用于 沿新轴堆叠多个数组 的函数，适用于将多个数组组合成一个更高维度的数组。以下是其用法详解：
#axis 的作用

#axis 值	堆叠方向	输入形状 (N个数组)	输出形状
#0	新维度作为第一个轴	(a, b) × N	(N, a, b)
#1	新维度作为第二个轴	(a, b) × N	(a, N, b)
#2	新维度作为第三个轴	(a, b) × N	(a, b, N)
#-1	新维度作为最后一个轴（默认）	(a, b) × N	(a, b, N)

def plot_points(X,Y):
    new_x = X[0, :]
    new_y = X[1, :]
    Y = np.squeeze(Y, 0)
    color_map = np.array(['r', 'g', 'b'])
    c = color_map[Y]
    plt.scatter(new_x, new_y, color = c)

    plt.show()

train_X, train_Y = generate_points(400)
print(train_X.shape)
print(train_Y.shape)
plot_points(train_X, train_Y)

数据预处理与PyTorch转换

在PyTorch中，所有参与运算的张量都用同一个类表示，其类型名叫做Tensor。而在构建张量时，我们一般用torch.tensor这个函数。

使用torch.tensor和使用np.ndarray非常类似，一般只要把数据传入第一个参数就行，有需要的话可以设置数据类型，对于train_X：

train_X_pt = torch.tensor(train_X, dtype=torch.float32)

而在使用train_Y时，要做一些额外的预处理操作。在计算损失函数时，PyTorch默认标签Y是一个一维整形数组。而我们之前都会把Y预处理成[1, m]的张量。因此，这里要先做一个维度转换，再转张量：

train_Y_pt = torch.tensor(train_Y.squeeze(0), dtype=torch.long)

 经过上述操作，X, Y再被送入PyTorch模型之前的形状是：

print(train_X_pt.shape)
print(train_Y_pt.shape)

# X: [2, m]
# Y: [m]

PyTorch多分类模型 

处理完了数据，接下来，我们就要定义神经网络了。在神经网络中，我们要实现初始化、正向传播、误差、评估这四个方法。

class MulticlassClassficationNet():
    def __init__(self, neuron_cnt: List[int]):
        self.num_layer = len(neuron_cnt)-1
        self.neuron_cnt = neuron_cnt
        self.W = []
        self.b = []
        for i in range(self.num_layer):
            new_W = torch.empty(neuron_cnt[i+1], neuron_cnt[i]) #empty生成形状的空张量
            new_B = torch.empty(neuron_cnt[i+1], 1)
            torch.nn.init.kaiming_normal_(new_W, nonlinearity='relu')#kaiming_normal就是He Initialization
            torch.nn.init.kaiming_normal_(new_B, nonlinearity='relu')
            self.W.append(torch.nn.Parameter(new_W))#我们把它们 构造成torch.nn.Parameter。这样，torch就会自动更新这些参数了。
            self.b.append(torch.nn.Parameter(new_B))
        self.trainable_vars = self.W + self.b
        self.loss_fn = torch.nn.CrossEntropyLoss()
    def forward(self, X):
        A = X
        for i in range(self.num_layer):
            Z = torch.matmul(self.W[i], A) + self.b[i]
            if i == self.num_layer -1:
                A = F.softmax(Z,0)
            else:
                A = F.relu(Z)
        return A
    

    
    def loss(self, Y, Y_hat):
        return self.loss_fn(Y_hat.T, Y)

    def evaluate (self, X, Y, return_loss = False):
        Y_hat = self.forward(X)
        Y_predict = Y
        Y_hat_predict = torch.argmax(Y_hat, 0)
        res = (Y_predict ==  Y_hat_predict).float()
        accuracy = torch.mean(res)
        if return_loss:
            loss = self.loss(Y, Y_hat)
            return accuracy, loss
        else:
            return accuracy
        
def train(model: MulticlassClassficationNet,
          X,
          Y,
          steps,
          learning_rate,
          print_interval=100):
    optimizer = torch.optim.Adam(model.trainable_vars, learning_rate)
    for i in range(steps):
        Y_hat = model.forward(X)
        cost = model.loss(Y, Y_hat)
        optimizer.zero_grad()
        cost.backward()
        optimizer.step()
        if i % print_interval == 0:
            accuracy, loss = model.evaluate(X, Y, return_loss=True)
            print(f'Step: {i}')
            print(f'Accuracy: {accuracy}')
            print(f'Train loss: {loss}')

和之前一样，我们通过neuron_cnt指定神经网络包含输出层在内每一层的神经元数。之后，根据每一层的神经元数，我们就可以初始化参数W和b了。

使用PyTorch，我们可以方便地完成一些高级初始化操作。首先，我们用torch.empty生成一个形状正确的空张量。之后，我们调用torch.nn.init.kaiming_normal_的初始化函数。kaiming_normal就是He Initialization。这个初始化方法需要指定激活函数是ReLU还是LeakyReLU。我们之后要用ReLU，所以nonlinearity是那样填的。

初始化完成后，为了让torch知道这几个张量是用可训练的参数，我们把它们 构造成torch.nn.Parameter。这样，torch就会自动更新这些参数了。

最后，我们用self.trainable_vars = self.W + self.b记录一下所有待优化变量，并提前初始化一个交叉熵误差函数，为之后的优化算法做准备

正向传播中

在这份代码中,torch.matmul用于执行矩阵乘法，等价于np.dot。和NumPy里的张量一样，PyTorch里的张量也可以直接用运算符+来完成加法。

做完了线性层的运算后，我们可以方便地调用torch.nn.functional里的激活函数完成激活操作。在大多数人的项目中，torch.nn.functional会被导入简称成F。PyTorch里的底层运算函数都在F中，而构造一个函数类（比如刚刚构造的torch.nn.CrossEntropyLoss()再调用该函数类，其实等价于直接去运行F里的函数。

值得一提的是，PyTorch会自动帮我们计算导数。因此，我们不用在正向传播里保存中间运算结果，也不用再编写反向传播函数了

损失函数

由于之前已经初始化好了误差函数，这里直接就调用就行了：

def loss(self, Y, Y_hat):
    return self.loss_fn(Y_hat.T, Y)

self.loss_fn = torch.nn.CrossEntropyLoss()就是PyTorch的交叉熵误差函数，它也适用于多分类。由于这个函数要求第一个参数的形状为[num_samples, num_classes]，和我们的定义相反，我们要把网络输出Y_hat转置一下。第二个输入Y必须是一维整形数组，我们之前已经初始化好了，不用做额外操作，PyTorch会自动把它变成one-hot向量。做完运算后，该函数会自动计算出平均值，不要再手动求一次平均。

评估

首先，我们使用Y_hat = self.forward(X)，根据X算出估计值Y_hat。之后我们就要对Y和Y_hat进行比较了。

Y_hat只记录了分类成各个类别的概率，用向量代表了标签。为了方便比较，我们要把它转换回用整数表示的标签。这个转换函数是torch.argmax。

和数学里的定义一样，torch.argmax返回令函数最大的参数值。而对于数组来说，就是返回数组里值最大的下标值。torch.argmax的第一个参数是参与运算的张量，第二个参数是参与运算的维度。Y_hat的形状是[3, m]，我们要把长度为3的向量转换回标签向量，因此应该对第一维进行运算（即维度0）。

得到了Y_predict, Y_hat_predict后，我们要比对它们以计算准确率。这时，我们可以用Y_predict == Y_hat_predict得到一个bool值的比对结果。PyTorch的类型比较严格，bool值是无法参与普通运算的，我们要用.float强制类型转换成浮点型。

最后，用accuracy = torch.mean(res)就可以得到准确率了。

由于我们前面写好了loss方法，计算loss时直接调用方法就行了。

训练

PyTorch使用一系列的优化器来维护梯度下降的过程。我们只需要用torch.optim.Adam(model.trainable_vars, learning_rate)即可获取一个Adam优化器。构造优化器时要输入待优化对象，我们已经提前存好了。

接下来，我们看for s in range(step):里每一步更新参数的过程。

在PyTorch里，和可学习参数相关的计算所构成的计算图会被动态地构造出来。我们只要普通地写正向传播代码，求误差即可。

执行完cost = model.loss(Y, Y_hat)，整个计算图就已经构造完成了。我们调用optimizer.zero_grad()清空优化器，用cost.backward()自动完成反向传播并记录梯度，之后用optimizer.step()完成一步梯度下降。

可以看出，相比完全用NumPy实现，PyTorch用起来十分方便。只要我们用心定义好了前向传播函数和损失函数，维护梯度和优化参数都可以交给编程框架来完成。

实验：

train_X, train_Y = generate_points(400)
plot_points(train_X, train_Y)
plot_X = generate_plot_set()

n_x = train_X.shape[0]
neuron_cnt = [n_x, 10, 10, 3]
model = MulticlassClassficationNet(neuron_cnt)

train_X_pt = torch.tensor(train_X, dtype=torch.float32)
train_Y_pt = torch.tensor(train_Y.squeeze(0), dtype=torch.long)

print(train_X_pt.shape)
print(train_Y_pt.shape)
train(model, train_X_pt, train_Y_pt, 20000, 0.01, 1000)


plot_result = model.forward(torch.Tensor(plot_X))

plot_result = torch.argmax(plot_result, 0).numpy()

plot_result = np.expand_dims(plot_result, 0)

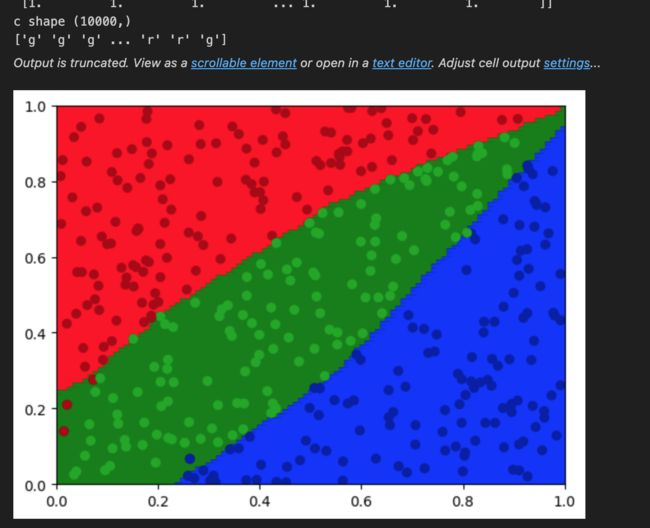
visualize(train_X, train_Y, plot_result)

网络训练完成后，我们用下面的代码把网络推理结果转换成可视化要用的NumPy结果：

plot_result = model.forward(torch.Tensor(plot_X))
plot_result = torch.argmax(plot_result, 0).numpy()
plot_result = np.expand_dims(plot_result, 0)

运行完plot_result = model.forward(torch.Tensor(plot_X))后，我们得到的是一个[3, m]的概率矩阵。我们要用torch.argmax(plot_result, 0)把它转换回整型标签。

def visualize(X, Y, plot_set_result: np.ndarray):
    x = np.linspace(0, 1, 100)
    y = np.linspace(0, 1, 100)

    xx, yy = np.meshgrid(x, y)
    color = plot_set_result.squeeze()

    color_map_1 = np.array(['r', 'g', 'b'])
    color_map_2 = ['#AA0000', '#00AA00', '#0000AA']

    c = color_map_1[color]

    plt.scatter(xx, yy, c=c, marker='s')
    
    plt.xlim(0, 1)
    plt.ylim(0, 1)

    origin_x = X.T[:, 0]
    origin_y = X.T[:, 1]
    origin_color = Y.squeeze(0)
    origin_color = [color_map_2[oc] for oc in origin_color]

    plt.scatter(origin_x, origin_y, c=origin_color)

    plt.show()