<密码学入门>关于DES加密算法解密算法相关问题
题外话:个人觉得DES加密解密真的是一种过程冗长的方法,S盒,P盒还有各种各样的变换让人眼花缭乱。
(一)Feistel密码结构
要先说Feistel密码结构的原因是DES加密过程是和Feistel密码结构完全一致的。
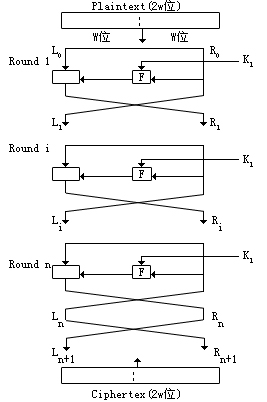
Feistel密码结构首先要将待加密的部分分为左右R0,L0,下一步的操作是将L0不做处理直接传递给R1,R0首先要经过一个轮函数F(Rx,Kx)的处理之后再和L0的每一位进行半加操作,一般情况下,在左右两部分不断交换的过程中,子密钥Kx也会不断地发生变化,实质上是使F(Rx,Kx)函数要进行的操作处理因为Kx的变化而改变。不断交换的过程也就使明文的统计特性分散到了密文之中,也就是所谓”混淆扩散“,其中轮函数F是整个加密过程中的唯一非线性部分,轮函数的复杂性决定了加密的程度。
代数表达Feistel密码结构就是:
(二)DES加密过程
DES算法处理的整个过程是将待加密的64bit明文,经过64BIT的密钥来进行加密,最后生成目标64bit的密文,加密过程具体如下:
1.第一步是从目标的文件或者buffer之中得到将要加密处理的文件指针或者指针,待加密的明文设为如下:
01 02 03 04 05 06 07 08
09 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
经过IP置换之后形成新的明文序列:(以下b均省略)
58 50 42 34 26 18 10 02
60 52 44 36 28 20 12 04
62 54 46 38 30 22 14 06
64 56 48 40 32 24 16 08
57 49 41 33 25 17 09 01
59 51 43 35 27 19 11 03
61 53 45 37 29 21 13 05
63 55 47 39 31 23 15 07
关于IP置换的具体过程网上的解释版本真的是很多,但是这并不妨碍我们的DES加密过程,因为将明文IP置换的过程就是一次遍历明文按索引的过程,我们只需要开出64*sizeof(char)的空间就可以完成初始的IP置换过程。易知在加密过程结束之中我们需要一次IP置换的逆置换(对于矩阵PAA^(-1)=P):
40 08 48 16 56 24 64 32 39 07 47 15 55 23 63 31 38 06 46 14 54 22 62 30 37 05 45 13 53 21 61 29 36 04 44 12 52 20 60 28 35 03 43 11 51 19 59 27 34 02 42 10 50 18 58 26 33 01 41 09 49 17 57 25
2.子密钥的生成过程
我们最先得到的所谓子密钥是64bit的,但是其中真正能够使用到的部分是48位的子密钥,其中经过了如下一次变换:
(PC-1置换的对应下标矩阵,首先去掉了每行的第8位奇偶校验位,然后进行置换)
57 49 41 33 25 17 09
01 58 50 42 34 26 18
10 02 59 51 43 35 27
19 11 03 60 52 44 36
-----------------------
63 55 47 39 31 23 15
07 62 54 46 38 30 22
14 06 61 53 45 37 29
21 13 05 28 20 12 04
经过了PC-1置换之后将得到的部分分为前28bit和后28bit分别为C0,D0
然后将C0,D0分别循环移位一位或者两位,具体的位数由下面这个数列决定
1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1
在DES的十六次迭代过程中,子密钥的生成过程严格按照上述顺序进行,如果要将每次循环移位后得到的数据使用到轮函数中作为参数的话,我们需要另一个压缩置换矩阵PC-2下标矩阵如下:
14 17 11 24 01 05
03 28 15 06 21 10
23 19 12 04 26 08
16 07 27 20 13 02
41 52 31 37 47 55
30 40 51 45 33 48
44 49 39 56 34 53
46 42 50 36 29 32
进行PC-2压缩置换之后我们得到的是48位的子密钥,至于怎么用进轮函数之中,下文会有具体介绍。总而言之子密钥的不断迭代生成过程可以用如下图表表示:
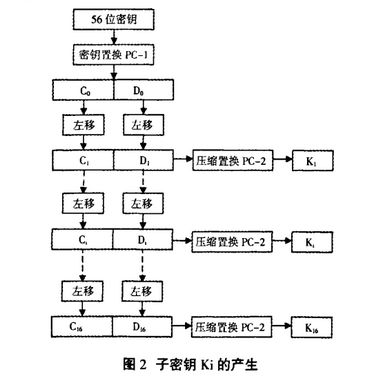
3.关于轮函数F(Rx,Kx)内部
首先轮函数接受的参数有两个一个是待加密的32bit串,另一个是48位的当前迭代轮生成的子密钥,运算过程如下:
(1)膨胀过程,将32bit的待加密串膨胀为48bit串,这一步也被叫做扩展置换,扩展置换的实质是把32bit串的某些位进行重复出现从而实现扩展,扩展下标表如下所示:
32 01 02 03 04 05
04 05 06 07 08 09
08 09 10 11 12 13
12 13 14 15 16 17
16 17 18 19 20 21
20 21 22 23 24 25
24 25 26 27 28 29
28 29 30 31 32 01
这一过程也被称为“E盒”。之后将通过E盒得到的膨胀后的串和48位的子密钥进行抑或运算/半加运算,得到一个新48bit串
(2)S盒,这一步也是最关键的一步,因为这一步所进行的过程是完全非线性的,也是加密过程中的核心部分。将最新得到的48bit串按顺序分为8个6bit的串,每一个6bit通过一个对应的S盒产生一个4位的输出。具体的过程是这样的,从6bit串中取第一位和第六位合并合起来作为S盒的行坐标,剩下的四位作为列坐标,例如010111串的第一位是0第六位是1,那么行坐标就是01B列坐标就是1011B即0xB,S盒的每一对坐标都可以得到其中的4位数据如下图所示:
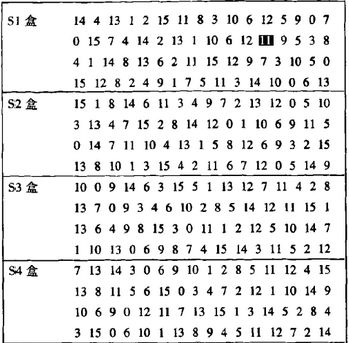

最后将从8个S盒得到的输出结果按顺序链接起来得到一个新的32bit串,再经过一个P盒变换产生一个新的32bit串,P盒变换和E盒变换的过程是相似的,下标矩阵如下:
16 07 20 21
29 12 28 17
01 15 23 26
05 18 31 10
02 08 24 14
32 27 03 09
19 13 30 06
22 11 04 25
这样的数据从P盒出来就是完成了轮函数的整个过程拉,出来的结果于另半部分合并后再经过16次循环后IP逆置换就得到了密文,下面是我自己绘制的程序框架:
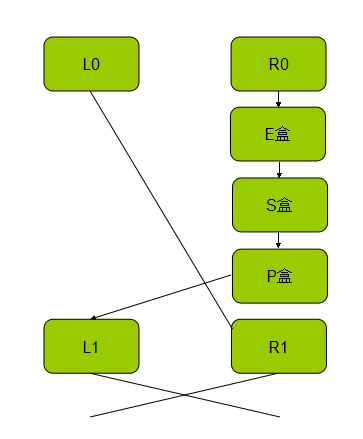
DES算法非常复杂,但是加密程度也非常高,严格遵循了雪崩效应 ,使密钥中一位的改动会导致子密钥的牵连改变从而完成混淆扩散的目的。
#################################
Problem1:证明DES算法的加密过程是解密过程的逆运算。
Ans:
DES算法遵守Feistel密码结构,因此有
Ri+1=Li
Li+1=Li⊕F(Ri,Ki)
解密过程中将Ri+1,Li+1代入上述式得(解密左右顺序是反的):
Li+1=Ri
Li+1⊕F(Ri,Ki)=Li⊕F(Ri,Ki)⊕F(Li+1,Ki)=Li⊕F(Ri,Ki)⊕F(Ri,Ki)=Li
因此代入后左右两边得到的结果是加密过程之中的上一轮的左右部分。