次小生成树 （附：poj1679）

 

次小生成树：

 

在求最小生成树时，用数组path[i][j]来表示MST中i到j最大边权。

求完后，直接枚举所有不在MST中的边，把它加入到MST中构成一棵新的树，且该树有环，此环是由刚加入的边(I,j)造成的，所以可以通过删除path[i][j]即可得到新的一颗树，且所有的该类树中必有一棵为次小生成树。

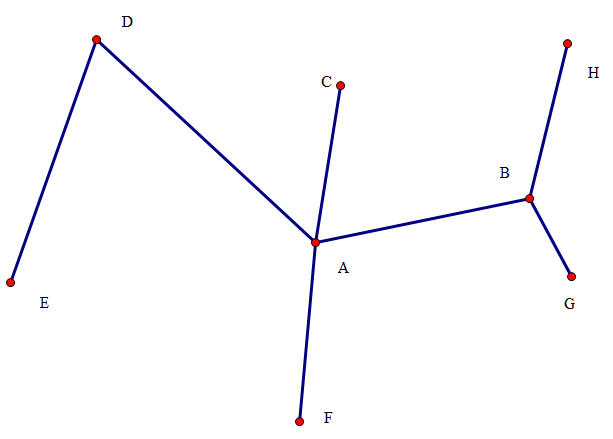
比如如图所示：

G,H不是MST上的边，通过加入边(G,H),得到一个环（B,H,G）,然后由于在计算最小生成树时已经计算出G,H之间最大边权为path[G][H] = BH，所以通过删除BH即可得到一棵此时最小的生成树，然后更新答案即可

#include <iostream>

#include <cstring>

#include <cstdio>



using namespace std;



const int X = 105;

const int INF = 100000000;



int map[X][X],dis[X]；

int path[X][X];///记录i,j路径上的最大边权

int pre[X];///前驱顶点

int n;  ///顶点数

bool use[X],in[X][X];



int prim()

{

    memset(use,false,sizeof(use));

    memset(pre,0,sizeof(pre));

    memset(in,false,sizeof(in));



    for(int i=0;i<=n;i++)

        dis[i] = INF;

    dis[1] = 0;

    int ans = 0;



    int MIN,k,p;

    for(int i=0;i<n;i++)

    {

        MIN = INF;

        for(int j=1;j<=n;j++)

            if(!use[j]&&MIN>dis[j])

                MIN = dis[k = j];

        if(MIN==INF)

            return INF;



        p = pre[k];

        in[p][k] = in[k][p] = true;

        path[p][k] = path[k][p] = MIN;//由于还没有算过顶点k，所以直接等于MIN



        for(int j=1;j<=n;j++)

            if(use[j])  //更新已经在MST中的顶点

                path[j][k] = path[k][j] = max(path[j][k],path[p][k]);



        use[k] = true;

        ans += MIN;



        for(int j=1;j<=n;j++)

            if(!use[j]&&dis[j]>map[k][j])

                dis[j] = map[k][j],pre[j] = k;

    }

    return ans;

}



int main()

{

    //freopen("sum.in","r",stdin);

    //freopen("sum.out","w",stdout);

    int t,m,x,y,z;

    cin>>t;

    while(t--)

    {

        scanf("%d%d",&n,&m);

        for(int i=1;i<=n;i++)

            for(int j=1;j<=n;j++)

                map[i][j] = map[j][i] = INF;

        while(m--)

        {

            scanf("%d%d%d",&x,&y,&z);

            map[x][y] = map[y][x] = z;

        }

        int ans = prim();

        int ok = true;

        for(int i=1;i<=n&&ok;i++)    //枚举找到不在MST上的边

            for(int j=1;j<=n&&ok;j++)

                if(map[i][j]!=INF&&!in[i][j])

                    if(ans==ans-path[i][j]+map[i][j])

                        ok = false;

        if(ok)

            printf("%d\n",ans);

        else

            printf("Not Unique!\n");

    }

    return 0;

}