poj2411 2663 2420 dp+状态压缩(多米诺骨牌问题)
题目描述:用1*2 的矩形通过组合拼成大矩形,求拼成指定的大矩形有几种拼法。
首先 我们先求用1*2 的矩形拼成 n*m的矩形有多少种拼法
当n*m为奇数时,一定是不会拼出来的,因为想要拼出来就需要整数倍的小矩形数目。
为了加速算法,要把m,n中小的那个当做列
分两个步骤:1) 先求出相邻两行的转化关系
2) 通过相邻两行的转化关系算出经过n次转化有几种方法能拼成n*m的矩阵
1) 状态标记 横放和竖放的下一个均为1,竖放的上一个和不放置为0 ,每行可以转化为1个2进制数。当这一行访问结束时,就会得到上一行状态,和该行状态,因为所有情况都是我们设置的,所以pre状态一定会转化为now状态
对于每一个位置,我们有三种放置方法:1. 竖直放置2. 水平放置3. 不放置
d为当前列号 ,初始化d, now, pre都为0。now为当前行,pre为当前行的上一行
1. d = d + 1, now << 1 | 1, pre << 1; // 竖直放置,当前行该列为1,上一行该列置为为0
2. d = d + 2, now << 2 | 3, pre<< 2 | 3; // 横放 都为11
3. d = d + 1, now << 1, pre<< 1 | 1; // 上一行该列置为1,不能竖放,不放置的状态
因为转移状态有很多种,所以用dfs去枚举各种可行的状态。
下面是dfs实现:
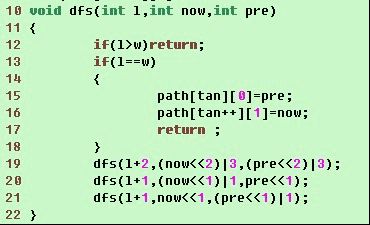
2) 求出来相邻两行之间的状态转化,下面就要求经过n次转化后最后状态为(1<<m - 1) 的总数,对于n比较小(可用矩阵存储) 的时候可用

当n很大的时候,就不能用上述的方法算了,这个时候矩阵的优势就体现出来了
同样是求经过n次转化,从初始态到终态有几种转化法
建立矩阵的方法很简单,矩阵的大小为(1<<m-1) 如过pre状态能到达状态now,那么++matrix[pre][now]; 然后求此矩阵的n次幂即可
1、poj2411 题意:给定一个长宽小于等于11的矩形,问用1×2的小矩形填满,有多少种方法。
#include <iostream>
#include <cstdio>
#include <cstring>
#define LL long long
using namespace std;
const int maxn=13;
int w,h,tan;
LL dp[13][2100];//1<<11
int path[14000][2];//11*(1<<11)
void dfs(int l,int now,int pre)
{
if(l>w)return;
if(l==w)
{
path[tan][0]=pre;
path[tan++][1]=now;
return ;
}
dfs(l+2,(now<<2)|3,(pre<<2)|3);
dfs(l+1,(now<<1)|1,pre<<1);
dfs(l+1,now<<1,(pre<<1)|1);
}
int main()
{
while(~scanf("%d%d",&h,&w))
{
if(!h&&!w)break;
if(h<w){int t=h;h=w;w=t;}
tan=0;
dfs(0,0,0);
memset(dp,0,sizeof(dp));
dp[0][(1<<w)-1]=1;
for(int i=0;i<h;++i)
{
for(int j=0;j<tan;++j)
{
dp[i+1][path[j][1]]+=dp[i][path[j][0]];
}
}
printf("%lld\n",dp[h][(1<<w)-1]);
}
return 0;
}
2、poj2663 题意:给定1*2的小矩形,去拼接一个3*n(n<30)的矩形,问有多少种方案。
3、poj3420 题意:给定1*2的小矩形,去拼接一个4*n(n<10^9)的矩形,问有多少种方案。N这么大递推肯定是不行了,所以我们要用矩阵快速幂进行加速,这个转移矩阵如何构造呢,我们可以直接用pre状态转移到now状态采用邻接矩阵的方式表述就好了。这个矩阵的大小为at[16][16],at[15][15]就是最后要求的状态
#include <iostream>
#include <cstdio>
#include <cstring>
#define LL long long
using namespace std;
struct mat{
LL at[16][16];
};
mat dat;
int n,mod;
void dfs(int l,int now,int pre)
{
if(l>4)return;
if(l==4)
{
++dat.at[pre][now];
return;
}
dfs(l+1,(now<<1)|1,(pre<<1));
dfs(l+1,(now<<1),(pre<<1)|1);
dfs(l+2,(now<<2)|3,(pre<<2)|3);
}
mat mul(mat a,mat b)
{
mat c;
memset(c.at,0,sizeof(c.at));
for(int i=0;i<16;++i)
{
for(int k=0;k<16;++k)
{
if(a.at[i][k])
{
for(int j=0;j<16;++j)
{
c.at[i][j]+=a.at[i][k]*b.at[k][j];
if(c.at[i][j]>=mod){c.at[i][j]%=mod;}
}
}
}
}
return c;
}
mat expo(mat a,int k)
{
if(k==1)return a;
mat e;
memset(e.at,0,sizeof(e.at));
for(int i=0;i<16;++i){e.at[i][i]=1;}
if(k==0)return e;
while(k)
{
if(k&1)e=mul(a,e);
a=mul(a,a);
k>>=1;
}
return e;
}
int main()
{
memset(dat.at,0,sizeof(dat.at));
dfs(0,0,0);
while(~scanf("%d%d",&n,&mod))
{
if(!n&&!mod)break;
if(mod==1){printf("0\n");continue;}
mat ans=expo(dat,n);
printf("%lld\n",ans.at[15][15]);
}
return 0;
}