hdu 3903 Trigonometric Function——数学题

打比赛的时候想这个题想了好长时间啊啊啊啊……后来谁知道这道题居然是神题啊啊啊啊……

官方题解：

引理 1:若 cosA 为有理数,n 为整数,则 cos(nA)也为有理数。

证:n=1,2 时,cos(nA)为有理。

若 n=1..k 时均成立,即 n<=k 时,cos(nA)为有理数,此时有 cos(kA) =

cos((k-1)A)*cos(A) - sin((k-1)A)*sin(A), sin((k-1)A)*sin(A)

故

有理。

当 n=k+1 时:

有 cos((k+1)A) = cos((k-1)A)*cos(2A) - sin((k-1)A)*sin(2A) =

cos((k-1)A)*cos(2A) - sin((k-1)A)*2*sinA*cosA.

由于 sin((k-1)A)*sin(A)与 cos(nA)(其中 n<=k)有理.

故 cos((k+1)A)有理,所以对所有正整数 n,cos(nA)为有理数,由此可得对

所有整数 n,cos(nA)为有理数。证毕。

引理 2:若 cosA 为有理数,则 sin(nA) = u*sinA,其中 u 为一有理数。

证:n=1 时成立。

若 n=k 成立,即 sin(kA)=u*sinA,其中 u 为有理数,则 sin((k+1)A) =

sin(kA)*cosA + sinA*cos(kA) , 由 引 理 1 得 cos(kA) 有 理 , 故

sin((k+1)A) = (u*cosA+cos(kA)) * sinA = v*sinA 中的 v 为有理

数,得证。

分子 cos(nA+mB) = cos(nA)*cos(mB) – sin(nA)*sin(mB)

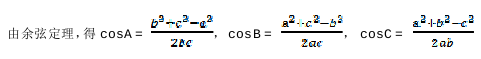
都是有理数,由引理 1 可得 cos(nA)*cos(mB)为有理数,由引理 2 得

sin(nA)*sin(mB) = u*sinA*v*sinB ,其中 u,v 均为有理数。又由三角

上代码：

2011-08-03 20:20:28  Accepted  3903  15MS  156K  669 B  G++  LadyTutu

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>

int check(long long n)
{
    long long i=ceil(sqrt(n))-1;
    for(;i*i<=n;i++)
    {
        if(i*i==n)
            return 1;
    }
    return 0;
}

long long gcd(long long a,long long b)
{
    if(b==0)
        return a;
    else return gcd(b,a%b);
}

int main(void)
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        long long a,b,c;
        int d,e,f;
        scanf("%I64d%I64d%I64d%d%d%d",&a,&b,&c,&d,&e,&f);
        if(check((a+b+c)*(a+b-c)*(a+c-b)*(b+c-a)))
            puts("YES");
        else puts("NO");
    }
}